La teoría de juegos es básicamente una rama de las matemáticas que se utiliza para la interacción estratégica típica entre diferentes jugadores (agentes), todos igualmente racionales, en un contexto con reglas predefinidas (de juego o maniobra) y resultados. Cada jugador o agente es una entidad racional que es egoísta y trata de maximizar la recompensa a obtener utilizando una estrategia particular. Todos los jugadores cumplen con ciertas reglas para recibir un desempate predefinido, una recompensa después de cierto resultado. Por lo tanto, un JUEGO se puede definir como un conjunto de jugadores, acciones, estrategias y un desempate final por el cual todos los jugadores compiten.
La teoría de juegos se ha convertido ahora en un factor descriptivo tanto para los algoritmos de aprendizaje automático como para muchas situaciones de la vida diaria.
Considere la SVM (Máquina de vectores de soporte) por ejemplo. Según Game Theory, el SVM es un juego entre 2 jugadores en el que un jugador desafía al otro a encontrar el mejor hiperplano después de proporcionar los puntos más difíciles para la clasificación. El desempate final de este juego es una solución que será un compromiso entre las habilidades estratégicas de ambos jugadores que compiten.
Tipos de Juegos:
Actualmente, existen alrededor de 5 tipos de clasificación de juegos. Son los siguientes:
- Juegos de suma cero y de suma distinta de cero: En los juegos de suma distinta de cero, hay múltiples jugadores y todos ellos tienen la opción de obtener un beneficio debido a cualquier movimiento de otro jugador. Sin embargo, en los juegos de suma cero, si un jugador gana algo, los otros jugadores están obligados a perder un desempate clave.
- Juegos simultáneos y secuenciales: los juegos secuenciales son los juegos más populares en los que cada jugador es consciente del movimiento de otro jugador. Los juegos simultáneos son más difíciles ya que en ellos los jugadores están involucrados en un juego concurrente. Los JUEGOS DE MESA son el ejemplo perfecto de juegos secuenciales y también se conocen como juegos por turnos o de forma extensiva.
- Juegos de información imperfecta e información perfecta: en un juego de información perfecta, cada jugador es consciente del movimiento del otro jugador y también de las diversas estrategias que el otro jugador podría estar aplicando para ganar el desempate final. Sin embargo, en los juegos de información imperfecta, ningún jugador es consciente de lo que el otro está haciendo. Las CARTAS son un ejemplo sorprendente de juegos de información imperfecta, mientras que el AJEDREZ es el ejemplo perfecto de un juego de información perfecta.
- Juegos asimétricos y simétricos: Los juegos asimétricos son aquellos en los que cada jugador tiene un objetivo final diferente y generalmente conflictivo. Los juegos simétricos son aquellos en los que todos los jugadores tienen el mismo objetivo final, pero la estrategia utilizada por cada uno es completamente diferente.
- Juegos cooperativos y no cooperativos: en los juegos no cooperativos, cada jugador juega por sí mismo, mientras que en los juegos cooperativos, los jugadores forman alianzas para lograr el objetivo final.
Equilibrio de Nash: El equilibrio
de Nash puede considerarse la esencia de la teoría de juegos. Es básicamente un estado, un punto de equilibrio de colaboración de múltiples jugadores en un juego. Nash Equilibrium garantiza el máximo beneficio para cada jugador.
Tratemos de entender esto con la ayuda de Generative Adversarial Networks (GAN).
¿Qué es GAN?
Es una combinación de dos redes neuronales: el Discriminador y el Generador. La red neuronal del generador recibe imágenes de entrada que analiza y luego produce nuevas imágenes de muestra, que se hacen para representar las imágenes de entrada reales lo más cerca posible. Una vez producidas las imágenes, se envían a la Red Neuronal Discriminadora. Esta red neuronal juzga las imágenes que se le envían y las clasifica como imágenes generadas e imágenes de entrada reales. Si la imagen se clasifica como la imagen original, la DNN cambia sus parámetros de evaluación. Si la imagen se clasifica como imagen generada, la imagen se rechaza y se devuelve a la GNN. Luego, el GNN altera sus parámetros para mejorar la calidad de la imagen producida.
Este es un proceso competitivo que continúa hasta que ambas redes neuronales no requieren realizar ningún cambio en sus parámetros y no puede haber más mejoras en ambas redes neuronales. Este estado de no mejora adicional se conoce como NASH EQUILIBRIO. En otras palabras, GAN es un juego competitivo de 2 jugadores en el que ambos jugadores se optimizan continuamente para encontrar un equilibrio de Nash.
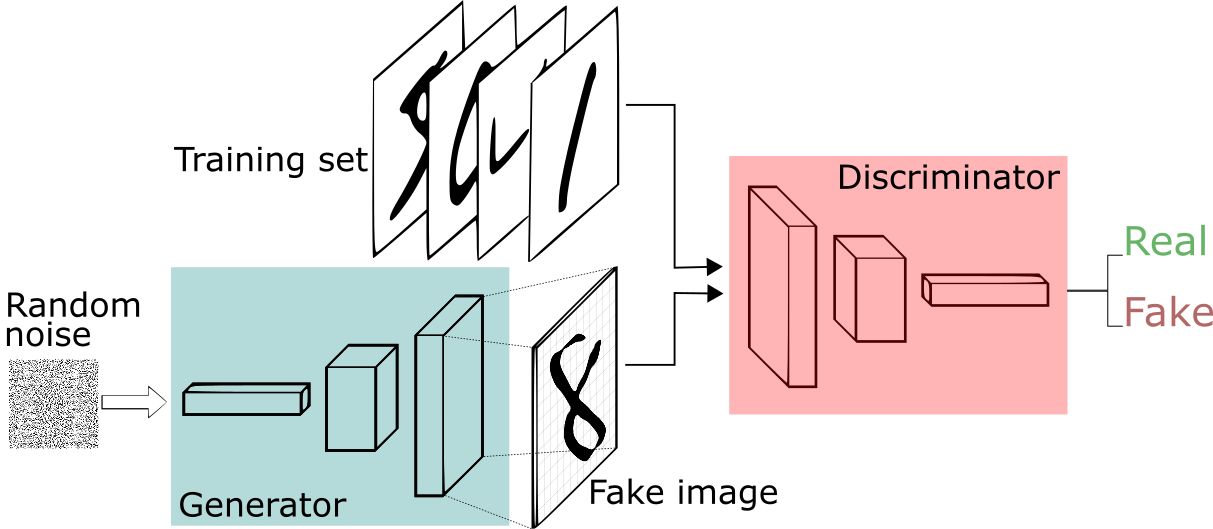
Pero, ¿cómo sabemos si el juego ha alcanzado el equilibrio de Nash?
En cualquier juego, se requiere que uno de los agentes revele su estrategia frente a los otros agentes. Tras la revelación, si ninguno de los jugadores cambia de estrategia, se entiende que el juego ha alcanzado el Equilibrio de Nash.
Ahora que conocemos los conceptos básicos de la teoría de juegos, intentemos comprender cómo se alcanza el equilibrio de Nash en un juego simultáneo. Hay muchos ejemplos, pero el más famoso es el Dilema del Prisionero. Hay algunos ejemplos más, como el juego de intercambio de bolsa cerrada, el juego Friend or For y el juego iterado Snowdrift.
En todos estos juegos participan dos jugadores y el desempate final es el resultado de una decisión que deben tomar ambos jugadores. Ambos jugadores tienen que elegir entre la deserción y la cooperación. Si ambos jugadores cooperan, el desempate final resultará positivo para ambos. Sin embargo, si ambos desertan, el desempate final será negativo para ambos jugadores. Si hay una combinación de un jugador que deserta y el otro coopera, el desempate final será positivo para uno y negativo para otro.
Aquí, el equilibrio de Nash juega un papel importante. Solo si ambos jugadores trazan una estrategia que los beneficie y les proporcione a ambos un desempate positivo, la solución a este problema será óptima.
Hay muchos más ejemplos reales y una serie de piezas de código que intentan resolver este dilema. La esencia básica, sin embargo, es el logro del Equilibrio de Nash en una situación incómoda.
¿Dónde está GAME THEORY ahora?
La teoría de juegos se está convirtiendo cada vez más en parte del mundo real en sus diversas aplicaciones en áreas como los servicios de salud pública, la seguridad pública y la vida silvestre. Actualmente, la teoría de juegos se está utilizando en el entrenamiento de adversarios en GAN, sistemas multiagente y aprendizaje por imitación y refuerzo. En el caso de información perfecta y juegos simétricos, son aplicables muchas técnicas de Machine Learning y Deep Learning. El verdadero desafío radica en el desarrollo de técnicas para manejar juegos con información incompleta, como el póquer. La complejidad del juego radica en el hecho de que hay demasiadas combinaciones de cartas y la incertidumbre de las cartas en manos de los distintos jugadores.