Teoría de Juegos (Normal – juego de forma) | Serie 1 (Introducción)

La teoría de juegos es un modelo matemático utilizado para la toma de decisiones. Tiene aplicaciones en todos los campos de las ciencias sociales, así como en la lógica y la informática. La teoría de juegos ha llegado a desempeñar un papel cada vez más importante en la lógica y en la informática. Para estar completamente definido, un juego debe especificar los siguientes elementos: los jugadores del juego, la información y las acciones disponibles para cada jugador en cada punto de decisión y los pagos para cada resultado. La mayoría de los juegos cooperativos se presentan en la forma de función característica, mientras que las formas extensiva y normal se utilizan para definir los juegos no cooperativos.

En teoría de juegos, la forma normal o también llamada forma estratégica, es una descripción de un juego. El juego normal (o de forma estratégica) suele estar representado por una array que muestra los jugadores, las estrategias y los pagos. Cuando un juego se presenta en forma normal, se presume que cada jugador actúa simultáneamente o, al menos, sin conocer las acciones del otro.

Situación
de toma de decisiones En general, la situación de toma de decisiones se puede clasificar en tres categorías diferentes, como se muestra en la siguiente figura: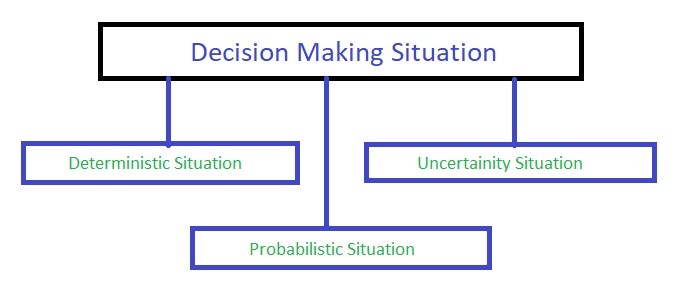

Terminologías básicas de la teoría de juegos

1. Jugadores : Generalmente hay dos jugadores en un juego. Por ejemplo, Jugador A y Jugador B, o Empresa A y Empresa B.
2. Estrategias : Estrategia significa que es un curso de acción tomado por un jugador, por ejemplo, una empresa tendrá diferentes estrategias para aumentar los volúmenes de ventas. Generalmente, en la teoría del juego hay dos estrategias, la primera estrategia pura y la segunda estrategia mixta . Si una empresa selecciona solo una estrategia en particular dejando la estrategia restante, entonces se dice que es una estrategia pura , pero la suma de estas probabilidades siempre es igual a 1 (ver el ejemplo a continuación). Si el jugador sigue más de una estrategia, entonces se dice que el jugador sigue una estrategia mixta, y donde la probabilidad de selección de una estrategia particular o individual es siempre menor que uno, por lo que la suma de todas las probabilidades será igual a 1 ( ver ejemplo a continuación).

   Ejemplo: Supongamos que hay tres estrategias S1, S2 y S3 .

   Estrategia pura : cuando el jugador selecciona una estrategia, digamos S2, entonces la probabilidad de S2 se convierte en 1 y la probabilidad de las dos estrategias restantes será 0. Por lo tanto, la suma de la probabilidad total es 0 + 1 + 0 = 1.

   Estrategia mixta : cuando un jugador selecciona dos estrategias, digamos S1 y S3, y sus probabilidades se dan como 0,62 y 0,38 respectivamente, y la probabilidad de la estrategia S2 es 0. Por lo tanto, la suma de la probabilidad total es 0,62 + 0 + 0,38 = 1.

3. Array de pagos: A continuación se muestra una array de pagos de muestra. Hay dos jugadores, el jugador A y el jugador B con tres estrategias cada uno, es decir, 1, 2 y 3. Los valores internos de la array son el resultado de diferentes combinaciones. Si el jugador A selecciona la 3.ª estrategia y el jugador B selecciona la 1.ª estrategia, el resultado será 35, y si el jugador A selecciona la 2.ª estrategia y el jugador B también selecciona la 2.ª estrategia, el resultado será 15.
   
   Si el el resultado es positivo, entonces es una ganancia para el jugador A y una pérdida para el jugador B. Si el resultado es negativo, entonces es una pérdida para el jugador A y una ganancia para el jugador B. Considere la siguiente array de pagos, si el resultado es -25 entonces el jugador A pierde 25 puntos mientras que el jugador B gana 25 puntos.
   
4. Principio Maximin : Maximiza las ganancias mínimas garantizadas.
5. Principio Minimax : Minimiza las pérdidas máximas.
6. Punto de silla : El juego tendrá punto de silla si el valor maximin y el valor minimax son iguales , es decir, el punto de intersección será igual. Cuando no hay un punto de silla en el juego, se dice que el juego tiene una estrategia mixta.
7. Valor del juego : si el juego tiene el punto silla, entonces el resultado en la celda en el punto silla se llama valor del juego.
8. Juego de suma cero para dos personas : en un juego con dos jugadores, si la ganancia de un jugador es igual a la pérdida de otro jugador, ese juego se denomina juego de suma cero para dos personas. Para una mejor comprensión, vea la array de pagos anterior, si el resultado del juego es 40, entonces es una ganancia para el jugador A pero una pérdida para el jugador B, y si el resultado es -25, entonces es una pérdida para el jugador A pero gana para el jugador. B.