El teorema o expansión del binomio describe la expansión algebraica de las potencias de un binomio. De acuerdo con este teorema, es posible expandir el polinomio “ (a + b) n ” en una suma que involucra términos de la forma “ ax z y c ” , los exponentes z y c son números enteros no negativos donde z + c = n, y el coeficiente de cada término es un número entero positivo dependiendo de los valores de n y b.
Ejemplo: Si n = 4
(a + b) 4 = un 4 + 4a 3 y + 6a 2 segundo 2 + 4ab 3 + segundo
Término General de Expansión Binomial
El Término General de Expansión Binomial de (x + y) n es el siguiente

- T r+1 es el Término General en la expansión binomial
- La expansión del término general se usa para encontrar los términos mencionados en la fórmula anterior.
- Para encontrar los términos en la expansión binomial, necesitamos expandir la expansión dada.
- Supongamos que (a + b) n es la ecuación, entonces la serie de su expansión binomial será la siguiente:
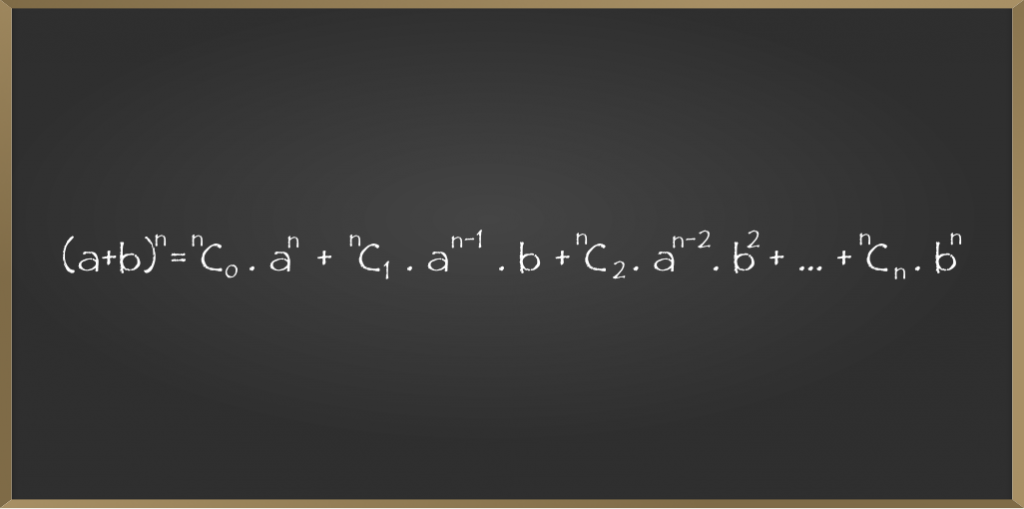
- El primer término de la serie es T 1 = n C 0 .a n
- El segundo término de la serie es T 2 = n C 1 .a n-1 .b
- El tercer término de la serie es T 3 = n C 2 .a n-2 .b 2
- El término n de la serie es T n = n C n .b n
Ejemplos de problemas sobre términos generales
Ejemplo 1: Encuentra (r+1) el término th para la expansión binomial dada (x + 2y) 5
Solución:
Dada la expansión es (x + 2y) 5
a = x, b = 2y, n = 5
La fórmula para (r+1) th es n C r .a n – r .b r
(r+1) th término = 5 C r .x 5 -r .2y r
Ejemplo 2: Encuentra (r+1) el término th para la expansión binomial dada (a + 2b) 7
Solución:
Dada la expansión es (a + 2b) 7
a = a, b = 2b, n = 7
La fórmula para (r+1)th es n C r .a n – r .b r
(r+1) th término = 7 C r .a 7 -r .b r
Ejemplo 3: Encuentra (r + 1) el término th para la expansión binomial dada (6p + 2q) 12
Solución:
Dada la expansión es (6p + 2q)
a = 6p, b = 2q, n = 12
La fórmula para (r+1) th es n C r .a n – r .b r
(r + 1) th término = 12 C r .6p 12 -r .2q r
Término medio de la expansión binomial
Si (x + y) n = n C r .x n – r. y r , tiene (n + 1) términos y el término medio dependerá del valor de n.
Tenemos dos casos para el Término Medio de una Expansión Binomial:
si n es par
Si n es el número par, lo convertimos en un número impar y consideramos (n + 1) como impar y (n/2 + 1) es el término medio. En simple, si n es par entonces lo consideramos impar.
Supongamos que n es par, entonces (n + 1) es impar. Para saber el término medio:
Considere el término general de expansión binomial, es decir

- Ahora reemplazamos «r» con «n/2» en la ecuación anterior para encontrar el término medio
- Tr +1 = Tn /2 + 1
- T n/2 + 1 = norte C n /2 .x norte – n/2 .y norte /2
Ejemplos de problemas en términos medios
Ejemplo 1: Encuentra el medio de la siguiente expansión binomial (x + a) 8
Solución:
Dada la expansión es (x + a) 8
n = 8, consideramos que la expansión tiene (n + 1) términos, por lo que la expansión anterior tiene (8 + 1), es decir, 9 términos
tenemos T 1 , T 2 , T 3 , T 4 , T 5 , T 6 , T 7 , T 8 , T 9 .
T r+1 = T n/2 + 1 = norte C n /2 .x norte – n/2 .Y norte /2
T 8/2 + 1 = 8 C 8/2 .x 8-8/2 .a 8/2
T 5 = 8 C 4 .x 4 .a 4 es el término medio requerido de la expansión binomial dada.
Ejemplo 2: Encuentra el medio de la siguiente expansión binomial (x + 3y) 6
Solución:
Dada la expansión es (x + 3y) 6
n = 6, consideramos que la expansión tiene (n + 1) términos, por lo que la expansión anterior tiene (6 + 1), es decir, 7 términos
tenemos T 1 , T 2 , T 3 , T 4 , T 5 , T 6 , T 7 .
T r+1 = T n/2 + 1 = norte C n /2 .x norte – n/2 .Y norte /2
T 6/2 + 1 = 6 C 6/2 .x 6-6/2 .3y 6/2
T 4 = 6 C 3 .x 3 .3y 3 es el término medio requerido de la expansión binomial dada.
Ejemplo 3: Encuentra el medio de la siguiente expansión binomial (2x + 5y) 4
Solución:
La expansión dada es (2x – 5y) 4
n = 4, consideramos que la expansión tiene (n + 1) términos, por lo que la expansión anterior tiene (4 + 1), es decir, 5 términos
tenemos T 1 , T 2 , T 3 , T 4 , T 5 .
T r+1 = T n/2 + 1 = norte C n /2 .x norte – n/2 .Y norte /2
T 4/2 + 1 = 4 C 4/2 .2x 4-4/2 .5y 4/2
T 3 = 4 C 2 .x 2 .5y 2 es el término medio requerido de la expansión binomial dada.
si n es impar
Si n es el número impar, lo convertimos en un número par y consideramos (n + 1) como par y (n + 1/2), (n + 3/2) son los términos medios. En simple, si n es impar entonces lo consideramos par.
Tenemos dos términos medios si n es impar. Para encontrar el término medio:
Considere el término general de expansión binomial, es decir

- En este caso, reemplazamos «r» con los dos valores diferentes
- Un término es (n + 1/2) en comparación con (r + 1) términos que obtenemos
r + 1 = norte + 1/2
r = norte + 1/2 -1
r = n-1/2
- Segundo término medio, compara (r + 1) con (n + 3/2) obtenemos
r+1 = n+3/2
r = norte + 3/2 – 1
r = norte + 1/2
Los dos términos medios cuando n es impar son (n – 1/2) y (n + 1/2) .
Ejemplos de problemas en términos medios
Ejemplo 1: Encuentra los términos medios de la siguiente expansión binomial (x + a) 9
Solución:
Dada la expansión es (x + a) 9
a = x, b = a y n = 9
Los términos medios serán (n – 1)/2 y (n + 1)/2
Tr + 1 =Tn – 1/2 y Tn + 1/2
Primer término medio:
T r + 1 = T n – 1/2 = 9 C (n – 1)/2 .x 9 – (n – 1)/2 .a (n – 1)/2
T (9 – 1/2) = 9 C (9 – 1)/2 .x 9 – (n – 1)/2 .a (n – 1)/2
T 4 = 9 C 4 .x 5 .a 4
Segundo término medio:
T r + 1 = T n + 1/2 = 9 C (n + 1)/2 .x 9 – (n + 1)/2 .a (n + 1)/2
T (9 + 1)/2 = 9 C (9 + 1)/2 .x 9 – (9 + 1)/2 .a (9 + 1)/2
T 5 = 9 C 5 .x 4 .a 5
Los términos medios de la expansión son T 4 y T 5.
Ejemplo 2: Encuentra los términos medios de la siguiente expansión binomial (4a + 9b) 7
Solución:
Dada la expansión es (4a + 9b) 7
a = 4a,b = 9b y n = 7
los términos medios serán (n -1/2) y (n + 1/2)
Tr + 1 =Tn – 1/2 y Tn + 1/2
Primer término medio:
T r + 1 = T n – 1/2 = 7 C (n – 1)/2 .4a 7 – (n – 1)/2 .9b (n – 1)/2
T (7 – 1/2) = 7 C (7 – 1)/2 .4a 7 – (7 – 1)/2 .9b (7 – 1)/2
T 3 = 7 C 3 .4a 4 .9b 3
Segundo término medio:
T r + 1 = T (n + 1)/2 = 7 C (n + 1)/2 .4a 7 – (n + 1)/2 .9b (n + 1)/2
T (7 + 1)/2 = 7 C (7 + 1)/2 .4a 7 – (7 + 1)/2 .9b (7 + 1)/2
T 4 = 7 C 4 .4a 3 .9b 4
Los términos medios de expansión son T 3 y T 4 .
Ejemplo 3: Encuentra los términos medios de la siguiente expansión binomial (2x + 8y) 5
Solución:
La expansión dada es (2x + 8y) 5
a = 2x, b = 8y y n = 5
Los términos medios serán (n – 1)/2 y (n + 1)/2
T r + 1 = T (n – 1)/2 y T (n + 1)/2
Primer término medio:
T r + 1 = T (n – 1)/2 = 5 C (n – 1)/2 .2x 5 – (n – 1)/2 .8y (n – 1)/2
T (5 – 1)/2 = 5 C (5 – 1)/2 .2x 5 – (5 – 1)/2 .8y (5 – 1)/2
T 2 = 5 C 2 .2x 3 .8y 2
Segundo término medio:
T r + 1 = T (n + 1)/2 = 5 C (n + 1)/2 .2x 5 – (n + 1)/2 .8y (n + 1)/2
T (5 + 1)/2 = 5 C (5 + 1)/2 .2x 5 – (5 + 1)/2 .8y (5 + 1)/2
T 3 = 5 C 3 .2x 2 .8y 3
Los términos medios de expansión son T 2 y T 3 .
Publicación traducida automáticamente
Artículo escrito por kadiummanisha y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA