¿Cuándo se elige la regresión?
Un problema de regresión es cuando la variable de salida es un valor real o continuo, como “salario” o “peso”. Se pueden usar muchos modelos diferentes, el más simple es la regresión lineal. Intenta ajustar los datos con el mejor hiperplano que pasa por los puntos.
El análisis de regresión es un proceso estadístico para estimar las relaciones entre las variables dependientes o variables de criterio y una o más variables independientes o predictores. El análisis de regresión explica los cambios en los criterios en relación con los cambios en los predictores seleccionados. La expectativa condicional de los criterios se basa en predictores donde se da el valor promedio de las variables dependientes cuando se cambian las variables independientes. Los tres usos principales del análisis de regresión son determinar la fuerza de los predictores, pronosticar un efecto y pronosticar tendencias.
Tipos de regresión:
- La regresión lineal se utiliza para el análisis predictivo. La regresión lineal es un enfoque lineal para modelar la relación entre el criterio o la respuesta escalar y los múltiples predictores o variables explicativas. La regresión lineal se centra en la distribución de probabilidad condicional de la respuesta dados los valores de los predictores. Para la regresión lineal, existe el peligro de sobreajuste. La fórmula para la regresión lineal es: Y’ = bX + A.
- La regresión polinomial se utiliza para datos curvilíneos. La regresión polinomial se ajusta con el método de mínimos cuadrados. El objetivo del análisis de regresión es modelar el valor esperado de una variable dependiente y con respecto a la variable independiente x. La ecuación para la regresión polinomial es: l =
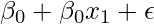 .
. - La regresión por pasos se utiliza para ajustar modelos de regresión con modelos predictivos. Se lleva a cabo automáticamente. Con cada paso, la variable se suma o resta del conjunto de variables explicativas. Los enfoques para la regresión por pasos son la selección hacia adelante, la eliminación hacia atrás y la eliminación bidireccional. La fórmula para la regresión paso a paso es
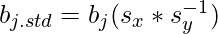 .
. - La regresión de cresta es una técnica para analizar datos de regresión múltiple. Cuando ocurre multicolinealidad, las estimaciones de mínimos cuadrados son imparciales. Se agrega un grado de sesgo a las estimaciones de regresión y, como resultado, la regresión de cresta reduce los errores estándar. La fórmula para la regresión de la cresta es
 .
. - La regresión de Lasso es un método de análisis de regresión que realiza tanto la selección como la regularización de variables. La regresión de Lasso utiliza un umbral suave. La regresión de Lasso selecciona solo un subconjunto de las covariables proporcionadas para su uso en el modelo final. La regresión de Lasso es
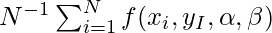 .
. - La regresión de ElasticNet es un método de regresión regularizado que combina linealmente las penalizaciones de los métodos de lazo y cresta. La regresión de ElasticNet se utiliza para máquinas de vectores de soporte, aprendizaje de métricas y optimización de carteras. La función de penalización viene dada por:
 .
.
A continuación se muestra la implementación simple:
Python3
# importing libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
x = 11 * np.random.random((10, 1))
# y = a * x + b
y = 1.0 * x + 3.0
# create a linear regression model
model = LinearRegression()
model.fit(x, y)
# predict y from the data where the x is predicted from the x
x_pred = np.linspace(0, 11, 100)
y_pred = model.predict(x_pred[:, np.newaxis])
# plot the results
plt.figure(figsize =(3, 5))
ax = plt.axes()
ax.scatter(x, y)
ax.plot(x_pred, y_pred)
ax.set_xlabel('predictors')
ax.set_ylabel('criterion')
ax.axis('tight')
plt.show()
Producción:
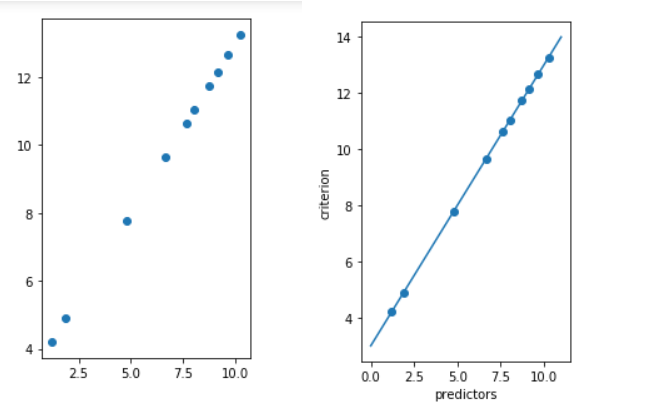
Publicación traducida automáticamente
Artículo escrito por Veena Ghorakavi y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA