Todos los números posibles de N dígitos y base B sin ceros a la izquierda

Dado un número de dígitos ‘N’ y base ‘B’, la tarea es contar todos los números de dígitos ‘N’ sin ceros a la izquierda que están en base ‘B’.

Ejemplos:  

Input: N = 2, B = 2
Output: 2
All possible numbers without 
leading zeros are 10 and 11.

Input: N = 5, B = 8
Output: 28672

Acercarse:  

• Si la base es ‘B’, cada dígito del número puede tomar cualquier valor dentro del rango [0, B-1].
• Por lo tanto, los números de dígitos B ‘N’ son posibles con la base ‘B’ (incluidos los números con ceros a la izquierda).
• Y, si fijamos el primer dígito como ‘0’, el resto de los dígitos ‘N-1’ pueden formar un total de 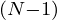números B.
• Entonces, el número total de números de dígitos ‘N’ con base ‘B’ posibles sin ceros a la izquierda es B – B .

A continuación se muestra la implementación del enfoque anterior: 

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// function to count
// all permutations
void countPermutations(int N, int B)
{
    // count of
    // all permutations
    int x = pow(B, N);
 
    // count of permutations
    // with leading zeros
    int y = pow(B, N - 1);
 
    // Return the permutations
    // without leading zeros
    cout << x - y << "\n";
}
 
// Driver code
int main()
{
 
    int N = 6;
    int B = 4;
 
    countPermutations(N, B);
 
    return 0;
}

// Java implementation of the approach
 
class GFG
{
// function to count
// all permutations
static void countPermutations(int N, int B)
{
    // count of
    // all permutations
    int x = (int)Math.pow(B, N);
 
    // count of permutations
    // with leading zeros
    int y = (int)Math.pow(B, N - 1);
 
    // Return the permutations
    // without leading zeros
    System.out.println(x - y);
}
 
// Driver code
public static void main(String[] args)
{
    int N = 6;
    int B = 4;
 
    countPermutations(N, B);
}
}
 
// This code is contributed by mits

# Python3 implementation of the approach
 
# function to count all permutations
def countPermutations(N, B):
 
    # count of all permutations
    x = B ** N
 
    # count of permutations
    # with leading zeros
    y = B ** (N - 1)
 
    # Return the permutations
    # without leading zeros
    print(x - y)
 
# Driver code
if __name__ == "__main__":
 
    N, B = 6, 4
    countPermutations(N, B)
 
# This code is contributed by Rituraj Jain

// C# implementation of the approach
 
using System;
class GFG
{
// function to count
// all permutations
static void countPermutations(int N, int B)
{
    // count of
    // all permutations
    int x = (int)Math.Pow(B, N);
 
    // count of permutations
    // with leading zeros
    int y = (int)Math.Pow(B, N - 1);
 
    // Return the permutations
    // without leading zeros
    Console.WriteLine(x - y);
}
 
// Driver code
public static void Main()
{
    int N = 6;
    int B = 4;
 
    countPermutations(N, B);
}
}
 
// This code is contributed
// by Akanksha Rai(Abby_akku)

<?php
// PHP implementation of the approach
 
// function to count all permutations
function countPermutations($N, $B)
{
    // count of all permutations
    $x = pow($B, $N);
 
    // count of permutations
    // with leading zeros
    $y = pow($B, $N - 1);
 
    // Return the permutations
    // without leading zeros
    echo ($x - $y), "\n";
}
 
// Driver code
$N = 6;
$B = 4;
 
countPermutations($N, $B);
 
// This code is contributed
// by Sach_Code`
?>

<script>
 
// Javascript implementation of the approach
 
// function to count
// all permutations
function countPermutations(N, B)
{
    // count of
    // all permutations
    var x = Math.pow(B, N);
 
    // count of permutations
    // with leading zeros
    var y = Math.pow(B, N - 1);
 
    // Return the permutations
    // without leading zeros
    document.write( x - y );
}
 
// Driver code
var N = 6;
var B = 4;
countPermutations(N, B);
 
</script>

3072

Complejidad de tiempo: O(logn)
Espacio auxiliar: O(1)