Dado lo difícil que puede ser la traducción, no debería sorprender que los sistemas de traducción automática más efectivos se creen entrenando un modelo probabilístico con estadísticas adquiridas de un vasto corpus de texto. Este método no necesita una ontología complicada de ideas interlingua, gramáticas de idioma de origen y de destino hechas a mano, o un banco de árboles etiquetado a mano. Solo requiere datos en forma de traducciones de ejemplo a partir de las cuales se puede aprender un modelo de traducción. Determinamos la string de palabras ![]() que maximiza
que maximiza
![]()
Para convertir una frase de inglés (e) a francés (f)
El modelo de idioma de destino para el francés es ![]() , que indica la probabilidad de que una oración en particular esté en francés. El modelo de traducción,
, que indica la probabilidad de que una oración en particular esté en francés. El modelo de traducción, ![]() , indica la probabilidad de que una oración en inglés se traduzca a una oración en francés en particular. Del mismo modo,
, indica la probabilidad de que una oración en inglés se traduzca a una oración en francés en particular. Del mismo modo, ![]() es un modelo de traducción del inglés al francés.
es un modelo de traducción del inglés al francés.
¿Deberíamos trabajar en ![]() directamente, o deberíamos usar la regla de Bayes y trabajar en P(e|f)P(f)? Es más fácil modelar el dominio en la dirección causal en aplicaciones de diagnóstico como medicina:
directamente, o deberíamos usar la regla de Bayes y trabajar en P(e|f)P(f)? Es más fácil modelar el dominio en la dirección causal en aplicaciones de diagnóstico como medicina: ![]() en lugar de
en lugar de ![]() . Sin embargo, ambos enfoques son igualmente simples de traducir. Los investigadores utilizaron la regla de Bayes en los primeros trabajos de traducción automática estadística, en parte porque tenían un modelo de lenguaje decente,
. Sin embargo, ambos enfoques son igualmente simples de traducir. Los investigadores utilizaron la regla de Bayes en los primeros trabajos de traducción automática estadística, en parte porque tenían un modelo de lenguaje decente, ![]() , y querían utilizarlo, y en parte, porque tenían experiencia en reconocimiento de voz, que es un problema de diagnóstico. En este capítulo, seguimos su camino, aunque debemos señalar que el trabajo reciente en traducción automática estadística con frecuencia optimiza
, y querían utilizarlo, y en parte, porque tenían experiencia en reconocimiento de voz, que es un problema de diagnóstico. En este capítulo, seguimos su camino, aunque debemos señalar que el trabajo reciente en traducción automática estadística con frecuencia optimiza ![]() directamente, empleando un modelo más complejo que incorpora muchas de las propiedades del modelo de lenguaje.
directamente, empleando un modelo más complejo que incorpora muchas de las propiedades del modelo de lenguaje.

El modelo de lenguaje, ![]() , podría abordar cualquier nivel(es) en el lado derecho de la figura anterior, pero la técnica más simple y frecuente, como hemos visto antes, es desarrollar un modelo de n-grama a partir de un corpus francés. . Esto solo capta un sentido local parcial de las frases en francés, pero suele ser suficiente para una traducción rudimentaria.
, podría abordar cualquier nivel(es) en el lado derecho de la figura anterior, pero la técnica más simple y frecuente, como hemos visto antes, es desarrollar un modelo de n-grama a partir de un corpus francés. . Esto solo capta un sentido local parcial de las frases en francés, pero suele ser suficiente para una traducción rudimentaria.
Un corpus bilingüe
Se utiliza una colección de textos paralelos, cada uno con un par inglés/francés, para entrenar el modelo de traducción. Si tuviéramos un corpus infinitamente grande, traducir una oración sería solo una tarea de búsqueda: ya habíamos visto la oración en inglés en el corpus, así que solo devolveríamos la oración en francés correspondiente. Sin embargo, nuestros recursos son limitados y la mayoría de las oraciones que tendremos que traducir no serán familiares. Sin embargo, estarán compuestos por términos que hemos visto anteriormente (incluso si algunas frases son tan cortas como una palabra). Por ejemplo, “en este ejercicio lo haremos”, “tamaño del espacio de estado”, “en función de” y “notas al final del capítulo” son términos predominantes en este libro. Deberíamos poder romper la oración nueva «En este ejercicio, calcularemos el tamaño del espacio de estado en función del número de acciones”. en frases, busque las frases correspondientes y las frases en francés en el corpus en inglés y en la traducción al francés respectivamente, y luego vuelva a ensamblar las frases en francés en un orden que tenga sentido en francés. Para decirlo de otra manera, dada una oración en inglés e, encontrar una traducción al francés f es un proceso de tres pasos:
- Divide la oración en inglés en

- 2 Elija una frase en francés
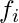 para cada frase
para cada frase 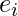 . Para la probabilidad frasal de que fi es una traducción de
. Para la probabilidad frasal de que fi es una traducción de 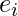 , usamos la notación
, usamos la notación 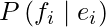 .
. - Elija una combinación de los términos
 . Esta permutación se especificará en un estilo que parece difícil pero que se supone que tiene una distribución de probabilidad simple: elegimos una distorsión
. Esta permutación se especificará en un estilo que parece difícil pero que se supone que tiene una distribución de probabilidad simple: elegimos una distorsión 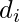 para cada
para cada 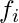 , que es el número de palabras que la frase fi se ha movido con respecto a
, que es el número de palabras que la frase fi se ha movido con respecto a  ; positivo para viajar a la derecha, negativo para moverse a la izquierda y cero si
; positivo para viajar a la derecha, negativo para moverse a la izquierda y cero si 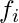 sigue
sigue  directamente.
directamente.
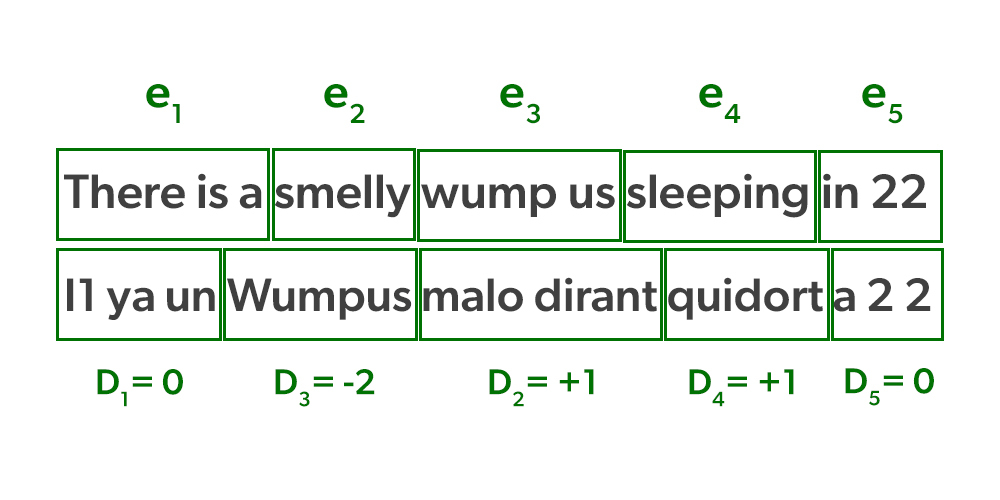
La figura anterior muestra un ejemplo del proceso explicado en el artículo anterior. La línea «Hay un wumpus apestoso durmiendo en 2 2″ se divide en cinco frases en la parte superior, ![]() . Cada uno se traduce en una
. Cada uno se traduce en una ![]() frase, que luego se permuta en el siguiente orden:
frase, que luego se permuta en el siguiente orden: ![]() . La permutación se define como
. La permutación se define como
![]()
donde ![]() es el número ordinal de la primera palabra de la frase
es el número ordinal de la primera palabra de la frase ![]() en la oración en francés y
en la oración en francés y ![]() es el número ordinal de la última palabra de la frase
es el número ordinal de la última palabra de la frase ![]() . La figura de arriba muestra que
. La figura de arriba muestra que ![]() viene justo después
viene justo después ![]() de , “qui dort”, por lo tanto
de , “qui dort”, por lo tanto ![]() .
. ![]() porque frase
porque frase ![]() se ha desplazado una palabra a la derecha de f1. Tenemos
se ha desplazado una palabra a la derecha de f1. Tenemos ![]() como caso especial ya que f1 comienza en la posición 1 y
como caso especial ya que f1 comienza en la posición 1 y ![]() se especifica que es 0. (aunque
se especifica que es 0. (aunque ![]() no existe).
no existe).
Podemos definir la distribución de probabilidad para la distorsión ![]() , ahora que hemos establecido la distorsión,
, ahora que hemos establecido la distorsión, ![]() . Debido a que tenemos
. Debido a que tenemos ![]() frases de longitud
frases de longitud ![]() , toda la distribución de probabilidad
, toda la distribución de probabilidad ![]() solo contiene
solo contiene ![]() elementos, significativamente menos números para recordar que el número de permutaciones,
elementos, significativamente menos números para recordar que el número de permutaciones, ![]() . Es por eso que la permutación se especificó de una manera tan enrevesada. Por supuesto, este es un modelo de distorsión bastante rudimentario. Al traducir del inglés al francés, no establece que los adjetivos se modifiquen con frecuencia para que aparezcan después del sustantivo; ese hecho se refleja en el modelo del idioma francés,
. Es por eso que la permutación se especificó de una manera tan enrevesada. Por supuesto, este es un modelo de distorsión bastante rudimentario. Al traducir del inglés al francés, no establece que los adjetivos se modifiquen con frecuencia para que aparezcan después del sustantivo; ese hecho se refleja en el modelo del idioma francés, ![]() . La probabilidad de distorsión no se ve afectada por las palabras de las oraciones, y se basa simplemente en el valor entero di. La distribución de probabilidad resume la volatilidad de la permutación; por ejemplo, con qué frecuencia es una distorsión de
. La probabilidad de distorsión no se ve afectada por las palabras de las oraciones, y se basa simplemente en el valor entero di. La distribución de probabilidad resume la volatilidad de la permutación; por ejemplo, con qué frecuencia es una distorsión de ![]() en comparación con
en comparación con ![]() .
.
Ahora es el momento de ponerlo todo junto: La probabilidad de que la serie de palabras f con distorsiones d sea una traducción de la secuencia de frases e puede definirse como ![]() . Suponemos que cada frase traducida y distorsionada es independiente de las demás, por lo que la expresión puede factorizarse como
. Suponemos que cada frase traducida y distorsionada es independiente de las demás, por lo que la expresión puede factorizarse como
![]()
Esto nos permite calcular la probabilidad de una traducción y distorsión ![]() candidatas dadas . Pero no podemos limitarnos a enumerar oraciones para descubrir la f y la d óptimas; con alrededor de 100 frases en francés para cada frase en inglés en el corpus, hay 100 5 distintas 5 traducciones y reordenaciones para cada una de ellas. Tendremos que buscar una solución decente. Encontrar una traducción casi más probable mediante una búsqueda de haz local con una heurística que evalúa la probabilidad ha demostrado ser beneficioso.
candidatas dadas . Pero no podemos limitarnos a enumerar oraciones para descubrir la f y la d óptimas; con alrededor de 100 frases en francés para cada frase en inglés en el corpus, hay 100 5 distintas 5 traducciones y reordenaciones para cada una de ellas. Tendremos que buscar una solución decente. Encontrar una traducción casi más probable mediante una búsqueda de haz local con una heurística que evalúa la probabilidad ha demostrado ser beneficioso.![]()
![]()
![]()
Lo único que queda es averiguar la probabilidad de distorsión y frase. Esbozamos el procedimiento para más información, lea las notas al final del capítulo
- Busca textos que sean similares: Para empezar, compila un corpus bilingüe en paralelo. Un Hansard9, por ejemplo, es un registro del discurso legislativo. Hansards bilingües se producen en Canadá, Hong Kong y otras naciones, la Unión Europea publica documentos oficiales en 11 idiomas y las Naciones Unidas producen publicaciones multilingües. El texto bilingüe en línea también está disponible; algunos sitios web publican material paralelo con direcciones URL paralelas, como /en/ para la página en inglés y /fr/ para la página en francés, por ejemplo. Cientos de millones de palabras de texto paralelo y miles de millones de palabras de material monolingüe se utilizan para entrenar algoritmos de traducción estadística.
- Dividir en oraciones: debido a que una oración es la unidad de traducción, necesitaremos dividir el corpus en oraciones. Los puntos son fuertes marcadores de la conclusión de una oración, sin embargo, en la línea “Dr. JR Smith de Rodeo Dr. pagó $29.99 el 9 de septiembre de 2009”, solo el punto final termina la oración. Un método para determinar si un punto termina una oración es entrenar un modelo que incluya las palabras circundantes y sus partes del discurso como características. Este método tiene una tasa de precisión del 98 por ciento.
- Alinear oraciones:Para cada oración en la versión en inglés, averigüe con qué oración(es) en la versión en francés se relaciona. En la mayoría de los casos, la siguiente oración en inglés corresponde a la siguiente oración en francés en una coincidencia 1:1, pero hay excepciones: una oración en un idioma puede dividirse en una coincidencia 2:1, o se puede cambiar el orden de dos oraciones. , resultando en una coincidencia 2:2. Usando una versión del método de Viterbi, es factible alinearlos (1:1, 1:2 o 2:2, etc.) con precisión en el rango de 90 a 99 por ciento simplemente observando la longitud de las oraciones (es decir, las oraciones cortas deben alinearse con oraciones cortas). Se puede obtener una alineación aún mayor empleando puntos de referencia comunes en ambos idiomas, como números, fechas, nombres propios o palabras con una traducción clara de un diccionario multilingüe.
- Alinear frases dentro de una oración: se puede utilizar un procedimiento similar al utilizado para la alineación de oraciones para alinear frases dentro de una oración, aunque se requiere una mejora iterativa. No tenemos forma de saber que «qui dort» se alinea con «dormir» cuando comenzamos, pero podemos llegar a esa conexión a través de un proceso de acumulación de evidencia. Podemos observar que “qui dort” y “dormir” coexisten a menudo en todas las oraciones de ejemplo y que ninguna otra frase distinta de “qui dort” coexiste con tanta frecuencia en otras oraciones con “dormir” en el par de oraciones alineadas. oraciones. Las probabilidades de frase están determinadas por una alineación de frase completa en nuestro corpus (después del suavizado apropiado).
- Defina la probabilidad de distorsión: una vez que tengamos una alineación de frase, podemos definir las probabilidades de distorsión. Simplemente cuente cuántas veces se distorsiona el corpus para cada distancia
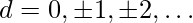 , luego suavícelo.
, luego suavícelo. - Use EM para mejorar las estimaciones: para mejorar las estimaciones de
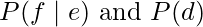 valores, use expectativa-maximización. En la
valores, use expectativa-maximización. En la  fase, calculamos las mejores alineaciones utilizando los valores de los parámetros actuales, luego actualizamos las estimaciones en el
fase, calculamos las mejores alineaciones utilizando los valores de los parámetros actuales, luego actualizamos las estimaciones en el 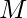 paso e iteramos el procedimiento hasta la convergencia.
paso e iteramos el procedimiento hasta la convergencia.
Publicación traducida automáticamente
Artículo escrito por Mohit Gupta_OMG 🙂 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA