Requisito previo: tipos básicos de transformación 2-D:
Transformación compuesta:
como su propio nombre sugiere Composición, aquí combinamos dos o más transformaciones en una sola transformación que es equivalente a las transformaciones que se realizan una tras otra sobre un objeto 2-D.
Ejemplo:
Considere que tenemos un objeto 2-D en el que primero aplicamos la transformación T 1 (condición de array 2-D) y luego aplicamos la transformación T 2 (condición de array 2-D) sobre el objeto 2-D y el objeto se transforma , el efecto muy equivalente sobre el objeto 2-D que podemos obtener multiplicando T 1 y T 2 (condiciones de la array 2-D) entre sí y luego aplicando el T 12 (resultante de T 1 XT 2 ) con las coordenadas del Imagen 2-D para obtener la imagen final transformada.
Problema:
Considere que tenemos un cuadrado O (0, 0), B (4, 0), C (4, 4), D (0, 4) en el que primero aplicamos T1 (transformación de escala) dado que el factor de escala es Sx = Sy = 0.5 y luego aplicamos T2 (transformación de rotación en el sentido de las agujas del reloj) en 90 * (ángulo), por último realizamos T3 (transformación de reflexión sobre el origen).
Respuesta: El cuadrado O, A, C, D se parece a:

Cuadrado_dado(Fig.1)
Primero, realizamos una transformación de escala sobre un objeto 2-D:
Representación de la condición de escala:
Para la coordenada O(0, 0) : ![Rendered by QuickLaTeX.com O\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}0.5&0\\0&0.5\end{bmatrix}*\begin{bmatrix}0\\0\end{bmatrix}\\\\[1ex]O\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9239e2812aa04726aaa25bc0f7c496b7_l3.png)
Para la coordenada B(4, 0) : ![Rendered by QuickLaTeX.com B\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}0.5&0\\0&0.5\end{bmatrix}*\begin{bmatrix}4\\0\end{bmatrix}\\\\[1ex]B\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}2\\0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1d6d6b8d64b9a9194195e9ce2140e1e2_l3.png)
Para la coordenada C(4, 4) : ![Rendered by QuickLaTeX.com C\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}0.5&0\\0&0.5\end{bmatrix}*\begin{bmatrix}4\\4\end{bmatrix}\\\\[1ex]C\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}2\\2\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-249a9f25b97f63cfba493ac3802c1a7a_l3.png)
Para la coordenada D(0, 4) : ![Rendered by QuickLaTeX.com D\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}0.5&0\\0&0.5\end{bmatrix}*\begin{bmatrix}0\\4\end{bmatrix}\\\\[1ex]D\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}0\\2\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dafdc4df5f487c81a4c203f4da4fc2dc_l3.png)
Objeto 2-D después de escalar:

Figura 2
*Ahora, realizaremos la transformación de rotación en el sentido de las agujas del reloj en la Fig.2 por 90 θ :
La condición de transformación de rotación de un objeto 2-D sobre el origen es:
Para la coordenada O(0, 0) : ![Rendered by QuickLaTeX.com O\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}0&1\\-1&0\end{bmatrix}*\begin{bmatrix}0\\0\end{bmatrix}\\\\[1ex]O\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8740ed087701f3ce398b335299627933_l3.png)
Para la coordenada B(2, 0) : ![Rendered by QuickLaTeX.com B\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}0&1\\-1&0\end{bmatrix}*\begin{bmatrix}2\\0\end{bmatrix}\\\\[1ex]B\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}0\\-2\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e7f35253c4fb6aee12938f21431e4fab_l3.png)
Para la coordenada C(2, 2) : ![Rendered by QuickLaTeX.com C\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}0&1\\-1&0\end{bmatrix}*\begin{bmatrix}2\\2\end{bmatrix}\\\\[1ex]C\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}2\\-2\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8b78d52bda514f6ab43f58932a7a55b2_l3.png)
Para la coordenada D(0, 2) : ![Rendered by QuickLaTeX.com D\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}0&1\\-1&0\end{bmatrix}*\begin{bmatrix}0\\2\end{bmatrix}\\\\[1ex]D\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}2\\0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ecba0668932cbbb328e74174cae068a6_l3.png)
Objeto 2-D después de girar sobre el origen en un ángulo de 90 * :

Fig. 3
*Ahora, realizaremos la tercera última operación en la Fig.3, reflejándola sobre el origen:
La condición de reflejar un objeto sobre el origen es
Para la coordenada O(0, 0) : ![Rendered by QuickLaTeX.com O\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}-1&0\\0&-1\end{bmatrix}*\begin{bmatrix}0\\0\end{bmatrix}\\\\[1ex]O\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-088a48b8b3992714fb34cd14b42307a4_l3.png)
Para la coordenada B'(0, 0) : ![Rendered by QuickLaTeX.com B'\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}0&-1\\-1&0\end{bmatrix}*\begin{bmatrix}0\\2\end{bmatrix}\\\\[1ex]B'\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}-2\\0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0b8202f778ded8e91429128f4fee45fa_l3.png)
Para la coordenada C'(0, 0) : ![Rendered by QuickLaTeX.com C'\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}-1&0\\0&-1\end{bmatrix}*\begin{bmatrix}2\\-2\end{bmatrix}\\\\[1ex]C'\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}-2\\2\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2e030f22127cf3bf4522d3d76d07f211_l3.png)
Para la coordenada D'(0, 0) : ![Rendered by QuickLaTeX.com D'\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}-1&0\\0&-1\end{bmatrix}*\begin{bmatrix}0\\-2\end{bmatrix}\\\\[1ex]D'\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}0\\2\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa606e19a2242f4569fe8af659c73f22_l3.png)
El objeto 2-D final después de reflexionar sobre el origen, obtenemos:

Figura 4
Nota: El resultado final anterior de la Fig.4 , que obtenemos después de aplicar todas las transformaciones una tras otra de manera serial. También podríamos obtener el mismo resultado combinando todas las condiciones de la array bidimensional de transformación y multiplicándolas entre sí y obteniendo una resultante de la multiplicación (R). Luego, aplicando esa array resultante 2D (R) en cada coordenada del cuadrado dado (arriba). Por lo tanto, obtendrá el mismo resultado que tiene en la Fig.4.
Solución utilizando la transformación compuesta:
*Primero multiplicamos las condiciones de la array 2-D de la transformación de escala con la transformación de rotación:
![Rendered by QuickLaTeX.com \begin{bmatrix}R_1\end{bmatrix}=\begin{bmatrix}0.5&0\\0&0.5\end{bmatrix}*\begin{bmatrix}0&1\\-1&0\end{bmatrix}\\\\[1ex]\begin{bmatrix}\\R_1\end{bmatrix}=\begin{bmatrix}0&0.5\\-0.5&0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fc06ff59b45aec3a1b211b5f00afc5a0_l3.png)
* Ahora, multiplicamos la array 2-D resultante (R 1 ) con la tercera última condición de transformación reflejada dada (R 2 ) para obtener la resultante (R):
![Rendered by QuickLaTeX.com \begin{bmatrix}R\end{bmatrix}=\begin{bmatrix}0&0.5\\-0.5&0\end{bmatrix}*\begin{bmatrix}-1&0\\0&-1\end{bmatrix}\\\\[1ex]\begin{bmatrix}\\R\end{bmatrix}=\begin{bmatrix}0&-0.5\\0.5&0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3702a7fb6fa94e918a50902daaa208ce_l3.png)
Ahora, aplicaremos la Resultante(R) de la array 2d en cada coordenada del objeto dado (cuadrado) para obtener el objeto final transformado o modificado.
La primera coordenada transformada O(0, 0) es: ![Rendered by QuickLaTeX.com O\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}0&-0.5\\0.5&0\end{bmatrix}*\begin{bmatrix}0\\0\end{bmatrix}\\\\[1ex]O\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ceec7e6792efb2480348cbaa6343a0e_l3.png)
En segundo lugar, la coordenada transformada B'(4, 0) es: ![Rendered by QuickLaTeX.com B'\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}0&-0.5\\0.5&0\end{bmatrix}*\begin{bmatrix}4\\0\end{bmatrix}\\\\[1ex]B'\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}0\\2\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7c5b550ae29ae7e9f52628fc76b315c4_l3.png)
La tercera coordenada transformada C'(4, 4) es: ![Rendered by QuickLaTeX.com C'\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}0&-0.5\\0.5&0\end{bmatrix}*\begin{bmatrix}4\\4\end{bmatrix}\\\\[1ex]C'\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}-2\\2\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3a896885609690c5a5d593d222b868cd_l3.png)
La cuarta coordenada transformada D'(0, 4) es: ![Rendered by QuickLaTeX.com D'\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}0&-0.5\\0.5&0\end{bmatrix}*\begin{bmatrix}0\\4\end{bmatrix}\\\\[1ex]D'\begin{bmatrix}\\x'\\y'\end{bmatrix}=\begin{bmatrix}-2\\0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a6b4c5371a89ee47e5abe1b8e03adb8c_l3.png)
El resultado final del objeto transformado que obtienes sería el mismo que el anterior:

Publicación traducida automáticamente
Artículo escrito por madhav_mohan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
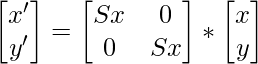
![Rendered by QuickLaTeX.com \begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}cosθ&sinθ\\-sinθ&cosθ\end{bmatrix}*\begin{bmatrix}x\\y\end{bmatrix}\\\\[1ex] Cos90 = 0 \\ sin90=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8bfaaf61941ba27ae54a0dedbbb875ac_l3.png)
![Rendered by QuickLaTeX.com \begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}-1&0\\0&-1\end{bmatrix}*\begin{bmatrix}x\\y\end{bmatrix}\\\\[1ex]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25d20077701c3efca8bb06909f27af60_l3.png)