Dados dos polinomios A(x) y B(x), encuentre el producto C(x) = A(x)*B(x). Ya existe un ![]() enfoque ingenuo de O() para resolver este problema. aquí _ Este enfoque utiliza la forma de coeficiente del polinomio para calcular el producto.
enfoque ingenuo de O() para resolver este problema. aquí _ Este enfoque utiliza la forma de coeficiente del polinomio para calcular el producto.
Una representación de coeficiente de un polinomio ![]() es a = a0, a1, …, an-1.
es a = a0, a1, …, an-1.
Ejemplo-![]()
![]()
Representación del coeficiente de A(x) = (9, -10, 7, 6)
Representación del coeficiente de B(x) = (-5, 4, 0, -2)
Input :
A[] = {9, -10, 7, 6}
B[] = {-5, 4, 0, -2}
Output :
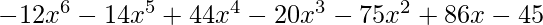
Podemos hacerlo mejor si representamos el polinomio de otra forma.
La idea es representar el polinomio en forma de valor puntual y luego calcular el producto. Una representación de valor puntual de un polinomio A(x) de grado n es un conjunto de n pares de valores puntuales { (x0, y0), (x1, y1), …, (xn-1, yn-1 )} tales que todos los xi son distintos y yi = A(xi) para i = 0, 1, …, n-1.
Ejemplo
xi -- 0, 1, 2, 3 A(xi) -- 1, 0, 5, 22
La representación de valor puntual del polinomio anterior es { (0, 1), (1, 0), (2, 5), (3, 22) }. Usando el método de Horner, ( discutido aquí ), la evaluación de n puntos toma tiempo O( ![]() ). Es solo el cálculo de los valores de A(x) en algún x para n puntos diferentes, por lo que la complejidad del tiempo es O(
). Es solo el cálculo de los valores de A(x) en algún x para n puntos diferentes, por lo que la complejidad del tiempo es O(![]() ). Ahora que el polinomio se convirtió en valor de puntos, se puede calcular fácilmente C(x) = A(x)*B(x) nuevamente usando el método de Horner. Esto toma tiempo O(n). Un punto importante aquí es que C(x) tiene un límite de grado 2n, entonces n puntos darán solo n puntos de C(x), entonces para ese caso necesitamos 2n valores diferentes de x para calcular 2n valores diferentes de y. Ahora que se calculó el producto, la respuesta se puede volver a convertir en forma de vector de coeficientes. Para volver a la forma de vector de coeficientes, usamos el inverso de esta evaluación. La inversa de la evaluación se llama interpolación. La interpolación usando la fórmula de Lagrange da la forma de valor de punto a la forma de vector de coeficiente del polinomio. La fórmula de Lagrange es –
). Ahora que el polinomio se convirtió en valor de puntos, se puede calcular fácilmente C(x) = A(x)*B(x) nuevamente usando el método de Horner. Esto toma tiempo O(n). Un punto importante aquí es que C(x) tiene un límite de grado 2n, entonces n puntos darán solo n puntos de C(x), entonces para ese caso necesitamos 2n valores diferentes de x para calcular 2n valores diferentes de y. Ahora que se calculó el producto, la respuesta se puede volver a convertir en forma de vector de coeficientes. Para volver a la forma de vector de coeficientes, usamos el inverso de esta evaluación. La inversa de la evaluación se llama interpolación. La interpolación usando la fórmula de Lagrange da la forma de valor de punto a la forma de vector de coeficiente del polinomio. La fórmula de Lagrange es – 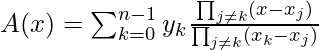
Hasta ahora discutimos,
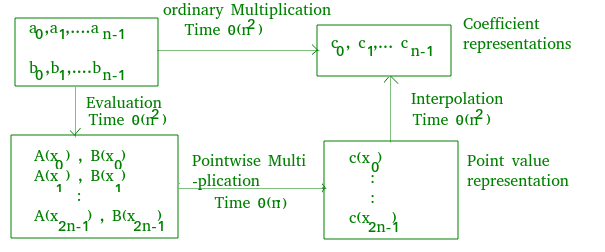
.
Esta idea aún resuelve el problema en la ![]() complejidad del tiempo O( ). Podemos usar cualquier punto que queramos como puntos de evaluación, pero al elegir los puntos de evaluación con cuidado, podemos convertir entre representaciones en solo tiempo O (n log n). Si elegimos «raíces complejas de la unidad» como puntos de evaluación, podemos producir una representación de valor de punto tomando la transformada discreta de Fourier (DFT) de un vector de coeficientes. Podemos realizar la operación inversa, la interpolación, tomando la «DFT inversa» de pares de puntos y valores, lo que produce un vector de coeficientes. Fast Fourier Transform (FFT) puede realizar DFT y DFT inversa en el tiempo O (nlogn).
complejidad del tiempo O( ). Podemos usar cualquier punto que queramos como puntos de evaluación, pero al elegir los puntos de evaluación con cuidado, podemos convertir entre representaciones en solo tiempo O (n log n). Si elegimos «raíces complejas de la unidad» como puntos de evaluación, podemos producir una representación de valor de punto tomando la transformada discreta de Fourier (DFT) de un vector de coeficientes. Podemos realizar la operación inversa, la interpolación, tomando la «DFT inversa» de pares de puntos y valores, lo que produce un vector de coeficientes. Fast Fourier Transform (FFT) puede realizar DFT y DFT inversa en el tiempo O (nlogn).
DFT
DFT está evaluando valores de polinomio en n raíces enésimas complejas de la unidad ![]() . Entonces, para
. Entonces, para ![]() k = 0, 1, 2, …, n-1, y = (y0, y1, y2, …, yn-1) es la Transformación de Fourier Discreta (DFT) del polinomio dado.
k = 0, 1, 2, …, n-1, y = (y0, y1, y2, …, yn-1) es la Transformación de Fourier Discreta (DFT) del polinomio dado.
El producto de dos polinomios de grado n es un polinomio de grado 2n. Por lo tanto, antes de evaluar los polinomios de entrada A y B, primero duplicamos sus límites de grado a 2n agregando n coeficientes de alto orden de 0. Debido a que los vectores tienen 2n elementos, usamos «raíces 2n-ésimas complejas de la unidad», que se denotan por el W2n (omega 2n). Suponemos que n es una potencia de 2; siempre podemos cumplir con este requisito agregando coeficientes cero de alto orden.
FFT
Esta es la estrategia divide y vencerás para resolver este problema.
Defina dos nuevos polinomios de n/2 con límites de grado, utilizando coeficientes de índice par e índice impar de A(x) por separado ![]()
![]()
![]()
El problema de evaluar A(x) en ![]() se reduce a evaluar los polinomios de n/2 con límites de grado A0(x) ) y A1(x) en los puntos
se reduce a evaluar los polinomios de n/2 con límites de grado A0(x) ) y A1(x) en los puntos ![]()
Ahora combinando los resultados por ![]()
La lista ![]() no contiene n valores distintos, sino n/2 complejas n/2 raíces de la unidad. Los polinomios A0 y A1 se evalúan recursivamente en las n raíces n-ésimas complejas de la unidad. Los subproblemas tienen exactamente la misma forma que el problema original, pero tienen la mitad del tamaño. Entonces la recurrencia formada es T(n) = 2T(n/2) + O(n), es decir, complejidad O(nlogn).
no contiene n valores distintos, sino n/2 complejas n/2 raíces de la unidad. Los polinomios A0 y A1 se evalúan recursivamente en las n raíces n-ésimas complejas de la unidad. Los subproblemas tienen exactamente la misma forma que el problema original, pero tienen la mitad del tamaño. Entonces la recurrencia formada es T(n) = 2T(n/2) + O(n), es decir, complejidad O(nlogn).
Algorithm 1. Add n higher-order zero coefficients to A(x) and B(x) 2. Evaluate A(x) and B(x) using FFT for 2n points 3. Pointwise multiplication of point-value forms 4. Interpolate C(x) using FFT to compute inverse DFT
Pseudocódigo de FFT recursiva
Recursive_FFT(a){
n = length(a) // a is the input coefficient vector
if n = 1
then return a
// wn is principle complex nth root of unity.
wn = e^(2*pi*i/n)
w = 1
// even indexed coefficients
A0 = (a0, a2, ..., an-2 )
// odd indexed coefficients
A1 = (a1, a3, ..., an-1 )
y0 = Recursive_FFT(A0) // local array
y1 = Recursive-FFT(A1) // local array
for k = 0 to n/2 - 1
// y array stores values of the DFT
// of given polynomial.
do y[k] = y0[k] + w*y1[k]
y[k+(n/2)] = y0[k] - w*y1[k]
w = w*wn
return y
}
Recursion Tree of Above Execution-

¿Por qué funciona esto? ![Rendered by QuickLaTeX.com y_{k} = y_{k}^{[0]} + \omega ^{k}_{n}y^{[1]}_{k}\newline y_{k} = A^{[0]}(\omega ^{2k}_{n})) + \omega ^{k}_{n}A^{[1]}(\omega ^{2k}_{n}) \newline y_{k} = A( \omega ^{k}_{n}) \newline \newline y_{k+(n/2)} = y_{k}^{[0]} - \omega ^{k}_{n}y^{[1]}_{k}\newline y_{k+(n/2)} = y_{k}^{[0]} + \omega ^{k+(n/2)}_{n} y_{k}^{[1]}\newline y_{k+(n/2)} = A^{[0]}(\omega ^{2k}_{n})) + \omega ^{k+(n/2)}_{n}A^{[1]}(\omega ^{2k}_{n})\newline y_{k+(n/2)} = A^{[0]}(\omega ^{2k+n}_{n})) + \omega ^{k+(n/2)}_{n}A^{[1]}(\omega ^{2k+n}_{n})\newline y_{k+(n/2)} = A^{[0]}(\omega ^{k+(n/2)}_{n}))](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-78b79ef6be882c429c2e0199bae51e58_l3.png)
ya que, por ![]()
lo tanto, el vector y devuelto por Recursive-FFT es de hecho el DFT del
vector de entrada a.
C++
#include <bits/stdc++.h>
using namespace std;
// For storing complex values of nth roots
// of unity we use complex<double>
typedef complex<double> cd;
// Recursive function of FFT
vector<cd> fft(vector<cd>& a)
{
int n = a.size();
// if input contains just one element
if (n == 1)
return vector<cd>(1, a[0]);
// For storing n complex nth roots of unity
vector<cd> w(n);
for (int i = 0; i < n; i++) {
double alpha = -2 * M_PI * i / n;
w[i] = cd(cos(alpha), sin(alpha));
}
vector<cd> A0(n / 2), A1(n / 2);
for (int i = 0; i < n / 2; i++) {
// even indexed coefficients
A0[i] = a[i * 2];
// odd indexed coefficients
A1[i] = a[i * 2 + 1];
}
// Recursive call for even indexed coefficients
vector<cd> y0 = fft(A0);
// Recursive call for odd indexed coefficients
vector<cd> y1 = fft(A1);
// for storing values of y0, y1, y2, ..., yn-1.
vector<cd> y(n);
for (int k = 0; k < n / 2; k++) {
y[k] = y0[k] + w[k] * y1[k];
y[k + n / 2] = y0[k] - w[k] * y1[k];
}
return y;
}
// Driver code
int main()
{
vector<cd> a{1, 2, 3, 4};
vector<cd> b = fft(a);
for (int i = 0; i < 4; i++)
cout << b[i] << endl;
return 0;
}
Python3
from math import sin,cos,pi # Recursive function of FFT def fft(a): n = len(a) # if input contains just one element if n == 1: return [a[0]] # For storing n complex nth roots of unity theta = -2*pi/n w = list( complex(cos(theta*i), sin(theta*i)) for i in range(n) ) # Separe coefficients Aeven = a[0::2] Aodd = a[1::2] # Recursive call for even indexed coefficients Yeven = fft(Aeven) # Recursive call for odd indexed coefficients Yodd = fft(Aodd) # for storing values of y0, y1, y2, ..., yn-1. Y = [0]*n middle = n//2 for k in range(n//2): w_yodd_k = w[k] * Yodd[k] yeven_k = Yeven[k] Y[k] = yeven_k + w_yodd_k Y[k + middle] = yeven_k - w_yodd_k return Y # Driver code if __name__ == '__main__': a = [1, 2, 3, 4] b = fft(a) for B in b: print(B)
Javascript
// JavaScript program to implement
// the approach
// For storing complex values of nth roots
// of unity we use complex
class complex
{
constructor(a, b = 0)
{
this.x = a;
this.y = b;
}
}
function product(c1, c2)
{
let c =new complex(0, 0);
c.x = c1.x * c2.x - c1.y * c2.y
c.y = c1.x * c2.y + c2.x * c1.y
return c
}
function sum(c1, c2)
{
let c = new complex(0, 0);
c.x = c1.x + c2.x
c.y = c1.y + c2.y
return c
}
function difference(c1, c2)
{
let c =new complex(0, 0);
c.x = c1.x - c2.x
c.y = c1.y - c2.y
return c
}
// Recursive function of FFT
function fft(a)
{
let n = a.length;
// if input contains just one element
if (n == 1)
return [a[0]]
// For storing n complex nth roots of unity
let w = new Array(n);
let alpha = -2 * Math.PI / n;
for (var i = 0; i < n; i++) {
w[i] = new complex(Math.cos(alpha * i), Math.sin(alpha * i));
}
let A0 = new Array(Math.floor(n / 2));
let A1 = new Array(Math.floor(n / 2));
for (var i = 0; i < Math.floor(n / 2); i++) {
// even indexed coefficients
A0[i] = a[i * 2];
// odd indexed coefficients
A1[i] = a[i * 2 + 1];
}
// Recursive call for even indexed coefficients
let y0 = fft(A0);
// Recursive call for odd indexed coefficients
let y1 = fft(A1);
// for storing values of y0, y1, y2, ..., yn-1.
let y = new Array(n);
for (var k = 0; k < Math.floor(n / 2); k++) {
y[k] = sum(y0[k], product(w[k], y1[k]));
y[k + Math.floor(n / 2)] = difference(y0[k], product(w[k], y1[k]));
}
return y;
}
// Driver code
let a = [ new complex(1, 0), new complex(2, 0), new complex(3, 0), new complex(4, 0)];
let b = fft(a);
for (var b0 of b)
console.log("(", b0.x, ",", b0.y, ")")
// This code is contributed by phasing17
Input: 1 2 3 4 Output: (10, 0) (-2, 2) (-2, 0) (-2,-2)
Interpolación
Cambia los roles de a e y.
Reemplace wn por wn^-1.
Divide cada elemento del resultado por n.
Complejidad de tiempo: O (nlogn).