Transformador disperso: zancada y atención factorizada fija

Los investigadores de @OpenAI propusieron la atención fija y a pasos agigantados en el artículo titulado ‘Generación de secuencias largas con transformadores dispersos’. Argumentan que Transformer es una arquitectura poderosa. Sin embargo, tiene el tiempo y el espacio computacionales cuadráticos frente a la longitud de la secuencia. Entonces, esto inhibe la capacidad de usar secuencias grandes. Es por eso que también proponen un nuevo transformador Sparse, que reduce la complejidad del tiempo a O(n ^(1+1/p) ) donde p>1 (p ~=2) al hacer algunos cambios en la arquitectura del Transformador,

También hicieron algunos cambios en el método de inicialización de peso y bloque residual para mejorar el entrenamiento de redes profundas.
Para calcular la array de atención de una manera más rápida y eficiente, también introdujeron un conjunto de kernels dispersos que calcula el subconjunto de manera eficiente.

Transformador estándar

En la figura de arriba, un transformador estándar procesando una imagen de 6×6 y 2 cabezales de atención. La fila de arriba indica una imagen de 6 × 6, que coloca dos cabezas de atención que reciben como entrada al calcular una salida determinada. La fila inferior indica la array de conectividad entre todas las salidas (filas) y entradas (columnas). Seguiremos esta convención en futuras imágenes también.

Arquitectura:

Consideremos un problema de generación de secuencias autorregresivas, donde la probabilidad conjunta de una distribución x ={x ₁ ,x ₂ ,..x _n } es el producto de la probabilidad condicional, parametrizada por $\ theta$

$p(x) = \prod_{i=1}^{n} p(x_i | x_1,x_2,x_3 ...x_{i-1} ; \theta)$

Aquí, las imágenes, el audio y el video también se pueden tratar como una secuencia de bytes sin formato.

La red toma la secuencia de entrada y genera una distribución categórica sobre v, donde v es el tamaño del vocabulario que se obtiene después de softmax en la salida de la red \theta.

Una buena elección para este tipo de modelo es el Transformer. Sin embargo, Transformer requiere una array de autoatención computacional que requiere computabilidad O(n ^{2 ).}Por lo tanto, los autores de este artículo hicieron algunas modificaciones a la arquitectura del transformador. Vamos a discutir estas modificaciones en detalle.

Auto atención factorizada:

Una array de autoatención asigna una incrustación de entrada a una array de salida y está parametrizada por el patrón de conectividad

$S = \left \S_1,S_2, ..., S_n{ \right \}$

donde, S_i denota el conjunto de índices del vector de entrada al que atiende el i ^-ésimo vector de salida. La autoatención se puede expresar mediante la siguiente expresión:

$Attend \left ( X,S \right ) = a\left ( a(x_i, S_i)\right )_{\left \{ i \epsilon i_1, i_2 ....i_n \right \}} \\ \\ a(x_i,S_i) = softmax(\frac{(W_q x_i) K_{S_i}^{T} }{\sqrt(d)}V_{S_i}) \\ \\ K_{S_i} = \left ( W_k x_j \right )_{j \epsilon S_i} \\ \\V_{S_i} = \left ( W_V x_j \right )_{j \epsilon S_i}$

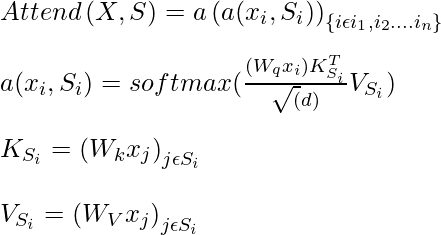
donde, W _q , W _k W _v son los pesos ,

En lugar de prestar atención a todos los valores anteriores antes de predecir el valor actual, los autores intentan realizarlo de manera más eficiente dividiendo todas las cabezas de atención en p cabezas de atención separadas, donde m ^th cabeza define el subconjunto de índices A_i^(m) A_i^( m) A_i^{(m)} \subset {j: j \leq i} y sea S_i =A_i^{(m)}. El objetivo del autor es dividir las cabezas de atención en un subconjunto eficiente para que

$\left |A_i^{(m)} \right | \propto \sqrt[p]{n}$

Además, el autor buscó opciones de A tales que p

Para cada par j<=i, i j p+1.

$j \epsilon A_{a}^{(1)} ; a \epsilon A_{b}^{(2)}; b \epsilon A_{c}^{(3)}$

Atención factorizada bidimensional:

Atención a zancadas:

Uno de los enfoques para predecir el píxel actual en dos dimensiones es que una cabeza atiende a l píxel anterior y la otra cabeza atiende a cada l ^-ésima ubicación donde l se llama zancada, y su valor se elige para que sea \sqrt{n} . En este patrón, el primer jefe asiste

La atención de la zancada se puede representar mediante las siguientes ecuaciones:

$A_i^{1} = \left \{ t, t+1, ... i \right \} ; for \, t = max\left ( 0,i-l \right ) \\ A_i^{2} = \left \{ j: \left ( i-j \right ) mod \, \, l =0 \right \}$

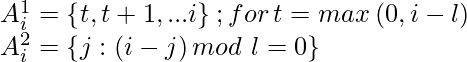
Este patrón de atención funciona cuando los datos tienen inherentemente algún tipo de patrón que se alinea con el paso, como datos de imágenes y datos de música. Esto no funcionará para conjuntos de datos que no contengan ningún patrón periódico y no comuniquen la información en blanco y negro.

Transformador disperso (a zancadas)

Atención fija:

En caso de falta de estructura y periodicidad en los datos, los autores proponen un método de factorización bidimensional llamado atención fija, donde celdas específicas resumen las ubicaciones anteriores y propagan la información a todas las celdas futuras. Esto se puede representar matemáticamente mediante las siguientes ecuaciones: $attention(X) = W_p \cdot attend(X,S)$

$A_{(i)}^{1} = \left \{ j: \lfloor{\frac{j}{l}} \rfloor = \lfloor{\frac{i}{l}} \rfloor \right \}$

$A_{(i)}^{2} = \left \{ j: j mod \,\, l \, \epsilon \left \{ t, t+1 , .. l-1 \right \} \right \}$

donde, t= lc y c es hiperparámetro.

Transformador disperso (fijo)

Transformador disperso:

Atención factorizada

La atención densa estándar realiza una transformación lineal de la función de atención:

$attention(X) = W_p \cdot attend(X,S)$

donde, W _p es la array de ponderación posterior a la atención. Sin embargo, a partir de los métodos anteriores, sabemos que tenemos más de un cabezal de atención, entonces, ¿cómo los integramos? El autor propone tres métodos para realizar esto:

La técnica más básica para integrar la autoatención factorizada es usar un tipo de atención por bloque residual e intercalarlos secuencialmente en una proporción, que puede determinarse mediante un hiperparámetro. La expresión matemática para este tipo de integración a continuación:

$attention(X) = W_p \cdot attend(X,A^{(r\, mod \, p)})$

Aquí, r es el bloque residual actual y p es un número de cabezas de atención.

Otro enfoque es hacer que un solo cabezal atienda las ubicaciones de los píxeles que atenderían ambos cabezales factorizados, que los autores fusionaron. Este enfoque es un poco más costoso computacionalmente.

$attention(X) = W_p \cdot attend(X,\bigcup_{m=1}^{P} \, A^{(m)})$

Un tercer enfoque que se utiliza en la atención de múltiples cabezas también es utilizado por los autores la mayor parte del tiempo. En este método, n _h productos de atención se calculan en paralelo y se concatenan a lo largo de la dimensión de la característica

$attention(X) = W_p\left ( attend(X, A)^{(i)} \right )_{i \epsilon \left \{ 1,2...,n_h \right \}} \\$

Escalado a 100 capas

Los autores de este artículo realizan algunos cambios importantes en la arquitectura para que sea más fácil entrenar el transformador de muchas capas, primero usan el bloque de preactivación similar al bloque residual que se usa en el papel ResNet.

$H_0 = embed(X ,W_e) \\ \\ H_k = H_{k-1} + resblock(H_{k-1}) \\ \\ Y = softmax(norm(H_N)W_{out})$

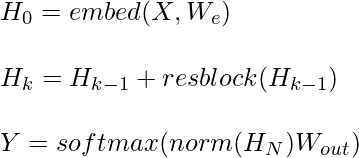
donde _Wout es la array de ponderaciones, resblock(h) normaliza la entrada y la posición de manera inteligente alimenta la atención de la siguiente manera:

$a(H) = dropout(attention(norm(H))) \\ b(H) = dropout(ff(norm(H + a(H)))) \\ resblock(H) = a(H) + b(H)$

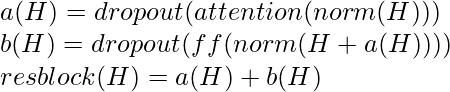
Aquí, la función norma denota la normalización de la capa, y ff es una función de activación, la elección correcta de ff es la unidad lineal de error de Gauss según los autores.

Modelado de diversos tipos de datos

Para codificar la relación espacial de los datos, el Transformador utiliza principalmente la incrustación basada en la posición y otra arquitectura específica de la ubicación. Los autores también concluyen que la incrustación en función de la posición es lo mejor para el modelo. Los autores calculan estas incrustaciones de la siguiente manera:

$embed (X, W_e) = \left ( x_i*W_e + \sum_{j=1}^{n_{emb}}o_{i}^{(j)}*W_j \right )_{x_i \epsilon X}$

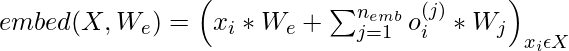
Donde n _emb = d _data (dimensión de datos) o n _emb = d _attn (dimensión de atención). Para los datos de imagen, n _emb =3 (d _data =3 ancho* alto* canales), para los datos de texto y audio, n _emb =2 porque d _attn =2 y el índice aquí corresponde al índice de fila y columna de cada posición en una array de ancho igual a la zancada. Aquí, x _i es el i- ^ésimo elemento codificado en caliente en la secuencia, y oi ( _j⁾ representa la posición codificada en caliente de x _i en la j ^-ésima dimensión.

Ahorro de memoria al volver a calcular los pesos de atención

El punto de control de gradiente fue la técnica ideada por los investigadores de OpenAI que permitía a los usuarios colocar modelos 10 veces más grandes en la GPU a costa de un 20 % de cálculos adicionales. Es particularmente efectivo para entrenar capas de autoatención cuando se procesan secuencias largas, ya que requieren un uso elevado de la memoria.

Usando solo el recálculo, los autores pueden ajustar una secuencia de longitud 16,384 (2 ^ 14) con 100 de la capa que, de otro modo, sería inviable incluso con la arquitectura moderna.

Núcleos de atención eficientes en bloques escasos:

de zancadasfijo

Los pesos de la red se almacenan en punto flotante de precisión simple, pero la activación de la red y los gradientes se calculan con precisión media. Esto nos ayuda a acelerar el entrenamiento del modelo en la GPU Nvidia V100.

Referencias

Papel transformador escaso

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA