Triángulo de Sierpinski

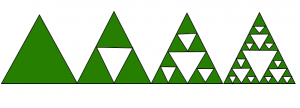
El triángulo de Sierpinski es un conjunto fijo fractal y atractivo con la forma general de un triángulo equilátero . Se subdivide recursivamente en triángulos más pequeños. 
 

Ejemplos: 
 

Input : n = 4
Output :
   * 
  * * 
 *   * 
* * * * 

Input : n = 8
Output :
       * 
      * * 
     *   * 
    * * * * 
   *       * 
  * *     * * 
 *   *   *   * 
* * * * * * * * 

Acercarse : 
 

El Triángulo de Sierpinski se construirá a partir de un triángulo equilátero mediante la eliminación repetida de subconjuntos triangulares. 
Pasos para la Construcción : 
1 . Tome cualquier triángulo equilátero. 
2 . Divídalo en 4 triángulos congruentes más pequeños y elimine el triángulo central. 
3 . Repita el paso 2 para cada uno de los triángulos más pequeños restantes para siempre. 
 

A continuación se muestra el programa para implementar el triángulo de sierpinski 
 

// C++ program to print sierpinski triangle.
#include <bits/stdc++.h>
using namespace std;
 
void printSierpinski(int n)
{
    for (int y = n - 1; y >= 0; y--) {
 
        // printing space till
        // the value of y
        for (int i = 0; i < y; i++) {
            cout<<" ";
        }
 
        // printing '*'
        for (int x = 0; x + y < n; x++) {
 
        // printing '*' at the appropriate position
        // is done by the and value of x and y
        // wherever value is 0 we have printed '*'
        if(x & y)
            cout<<" "<<" ";
        else
            cout<<"* ";
        }
 
        cout<<endl;
    }
}
 
// Driver code
int main()
{
    int n = 16;
 
    // Function calling
    printSierpinski(n);
 
    return 0;
}

// Java program to print
// sierpinski triangle.
import java.util.*;
import java.io.*;
 
class GFG
{
    static void printSierpinski(int n)
    {
        for (int y = n - 1; y >= 0; y--) {
 
            // printing space till
            // the value of y
            for (int i = 0; i < y; i++) {
                System.out.print(" ");
            }
 
            // printing '*'
            for (int x = 0; x + y < n; x++) {
 
                // printing '*' at the appropriate
                // position is done by the and
                // value of x and y wherever value
                // is 0 we have printed '*'
                if ((x & y) != 0)
                    System.out.print(" "
                                    + " ");
                else
                    System.out.print("* ");
            }
 
            System.out.print("\n");
        }
    }
 
    // Driver code
    public static void main(String args[])
    {
        int n = 16;
 
        // Function calling
        printSierpinski(n);
    }
}
 
// This code is contributed by Sahil_Bansall

# Python 3 program to print
# sierpinski triangle.
 
def printSierpinski( n) :
     
    y = n - 1
    while(y >= 0) :
         
        # printing space till
        # the value of y
        i = 0
        while(i < y ):
            print(" ",end="")
            i = i + 1
 
        # printing '*'
        x = 0
        while(x + y < n ):
 
            # printing '*' at the appropriate
            # position is done by the and
            # value of x and y wherever value
            # is 0 we have printed '*'
            if ((x & y) != 0) :
                print(" ", end = " ")
            else :
                print("* ", end = "")
            x =x + 1
         
        print()
        y = y - 1
         
# Driver code
n = 16
 
# Function calling
printSierpinski(n)
 
 
# This code is contributed by Nikita Tiwari.

// C# program to print
// sierpinski triangle.
using System;
 
class GFG {
    static void printSierpinski(int n)
    {
        for (int y = n - 1; y >= 0; y--) {
 
            // printing space till
            // the value of y
            for (int i = 0; i < y; i++) {
                Console.Write(" ");
            }
 
            // printing '*'
            for (int x = 0; x + y < n; x++) {
 
                // printing '*' at the appropriate
                // position is done by the and
                // value of x and y wherever value
                // is 0 we have printed '*'
                if ((x & y) != 0)
                    Console.Write(" " + " ");
                else
                    Console.Write("* ");
            }
 
            Console.WriteLine();
        }
    }
 
    // Driver code
    public static void Main()
    {
        int n = 16;
 
        // Function calling
        printSierpinski(n);
    }
}
 
// This code is contributed by vt_m

<?php
// PHP implementation to
// print sierpinski triangle.
 
function printSierpinski($n)
{
    for ($y = $n - 1; $y >= 0; $y--)
    {
 
        // printing space till
        // the value of y
        for ($i = 0; $i < $y; $i++)
        {
            echo " ";
        }
 
        // printing '*'
        for ($x = 0; $x + $y < $n; $x++)
        {
 
        // printing '*' at the appropriate
        // position is done by the and value
        // of x and y wherever value is 0 we
        // have printed '*'
        if($x & $y)
            echo"  ";
        else
            echo"* ";
        }
 
        echo "\n";
    }
}
 
// Driver code
$n = 16;
printSierpinski($n);
 
// This code is contributed by Mithun Kumar
?>

<script>
 
// javascript program to print
// sierpinski triangle.
 
function printSierpinski(n)
{
    for (var y = n - 1; y >= 0; y--) {
 
        // printing space till
        // the value of y
        for (var i = 0; i < y; i++) {
            document.write(" ");
        }
 
        // printing '*'
        for (var x = 0; x + y < n; x++) {
 
            // printing '*' at the appropriate
            // position is done by the and
            // value of x and y wherever value
            // is 0 we have printed '*'
            if ((x & y) != 0)
                document.write("   ");
            else
                document.write("* ");
        }
 
        document.write("<br>");
    }
}
 
// Driver code
var n = 16;
 
// Function calling
printSierpinski(n);
 
 
// This code contributed by Princi Singh
</script>

Producción : 
 

               * 
              * * 
             *   * 
            * * * * 
           *       * 
          * *     * * 
         *   *   *   * 
        * * * * * * * * 
       *               * 
      * *             * * 
     *   *           *   * 
    * * * *         * * * * 
   *       *       *       * 
  * *     * *     * *     * * 
 *   *   *   *   *   *   *   * 
* * * * * * * * * * * * * * * * 

Referencias: Wiki