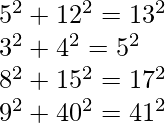El último teorema de Fermat

De acuerdo con el último teorema de Fermat , no hay tres números enteros positivos a, b, c que satisfagan la ecuación,  para cualquier valor entero de n mayor que 2. Para n = 1 y n = 2, la ecuación tiene infinitas soluciones.
 

Some solutions for n = 1 are,
 2 + 3 = 5
 7 + 13 = 20
 5 + 6 = 11
 10 + 9 = 19

Some solutions for n = 2 are,

// C++ program to verify fermat's last theorem
// for a given range and n.
#include <bits/stdc++.h>
using namespace std;
 
void testSomeNumbers(int limit, int n)
{
   if (n < 3)
     return;
 
   for (int a=1; a<=limit; a++)
     for (int b=a; b<=limit; b++)
     {
         // Check if there exists a triplet
         // such that a^n + b^n = c^n
         int pow_sum = pow(a, n) + pow(b, n);
         double c = pow(pow_sum, 1.0/n);
         int c_pow = pow((int)c, n);
         if (c_pow == pow_sum)
         {
             cout << "Count example found";
             return;
         }
     }
 
     cout << "No counter example within given"
            " range and data";
}
 
// driver code
int main()
{
    testSomeNumbers(10, 3);
    return 0;
}

// Java program to verify fermat's last theorem
// for a given range and n.
import java.io.*;
 
class GFG
{
    static void testSomeNumbers(int limit, int n)
    {
        if (n < 3)
            return;
         
        for (int a = 1; a <= limit; a++)
            for (int b = a; b <= limit; b++)
            {
                // Check if there exists a triplet
                // such that a^n + b^n = c^n
                int pow_sum = (int)(Math.pow(a, n)
                               + Math.pow(b, n));
                double c = Math.pow(pow_sum, 1.0 / n);
                int c_pow = (int)Math.pow((int)c, n);
                if (c_pow == pow_sum)
                {
                    System.out.println("Count example found");
                    return;
                }
            }
         
            System.out.println("No counter example within given"+
                               " range and data");
    }
     
    // Driver code
    public static void main (String[] args)
    {
        testSomeNumbers(12, 5);
     
    }
}
 
// This code is contributed by vt_m.

# Python3 program to verify fermat's last
# theorem for a given range and n.
 
def testSomeNumbers(limit, n) :
 
    if (n < 3):
        return
     
    for a in range(1, limit + 1):
        for b in range(a, limit + 1):
         
            # Check if there exists a triplet
            # such that a^n + b^n = c^n
            pow_sum = pow(a, n) + pow(b, n)
            c = pow(pow_sum, 1.0 / n)
            c_pow = pow(int(c), n)
             
            if (c_pow == pow_sum):
                print("Count example found")
                return
    print("No counter example within given range and data")
 
# Driver code
testSomeNumbers(10, 3)
 
# This code is contributed by Smitha Dinesh Semwal.

// C# program to verify fermat's last theorem
// for a given range and n.
using System;
 
class GFG {
     
    static void testSomeNumbers(int limit, int n)
    {
        if (n < 3)
            return;
         
        for (int a = 1; a <= limit; a++)
            for (int b = a; b <= limit; b++)
            {
                 
                // Check if there exists a triplet
                // such that a^n + b^n = c^n
                int pow_sum = (int)(Math.Pow(a, n)
                                + Math.Pow(b, n));
                double c = Math.Pow(pow_sum, 1.0 / n);
                int c_pow = (int)Math.Pow((int)c, n);
                 
                if (c_pow == pow_sum)
                {
                    Console.WriteLine("Count example found");
                    return;
                }
            }
         
            Console.WriteLine("No counter example within"
                                + " given range and data");
    }
     
    // Driver code
    public static void Main ()
    {
        testSomeNumbers(12, 3);
     
    }
}
 
// This code is contributed by vt_m.

<?php
// PHP program to verify fermat's
// last theorem for a given range
//and n.
 
function testSomeNumbers($limit, $n)
{
    if ($n < 3)
     
    for($a = 1; $a <= $limit; $a++)
        for($b = $a; $b <= $limit; $b++)
    {
         
        // Check if there exists a triplet
        // such that a^n + b^n = c^n
        $pow_sum = pow($a, $n) + pow($b, $n);
         
        $c = pow($pow_sum, 1.0 / $n);
        $c_pow = pow($c, $n);
        if ($c_pow != $pow_sum)
        {
            echo "Count example found";
            return;
        }
    }
 
    echo "No counter example within ".
              "given range and data";
}
 
    // Driver Code
    testSomeNumbers(10, 3);
 
// This code is contributed by m_kit
?>

<script>
 
// JavaScript program to verify fermat's last theorem
// for a given range and n.
 
    function testSomeNumbers(limit, n)
    {
        if (n < 3)
            return;
           
        for (let a = 1; a <= limit; a++)
            for (let b = a; b <= limit; b++)
            {
                // Check if there exists a triplet
                // such that a^n + b^n = c^n
                let pow_sum = (Math.pow(a, n)
                               + Math.pow(b, n));
                let c = Math.pow(pow_sum, 1.0 / n);
                let c_pow = Math.pow(Math.round(c), n);
                if (c_pow == pow_sum)
                {
                    document.write("Count example found");
                    return;
                }
            }
           
            document.write("No counter example within given"+
                               " range and data");
    }
  
 
// Driver Code
 
        testSomeNumbers(12, 5);
           
</script>

No counter example within given range and data

Complejidad de Tiempo: O(m ² logn) , donde m es el límite
Espacio Auxiliar: O(1)

Sugiera si alguien tiene una mejor solución que sea más eficiente en términos de espacio y tiempo.
Este artículo es una contribución de Aarti_Rathi . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.