El número complejo se define como el número de la forma a+ib, donde a es la parte real mientras que ib es la parte imaginaria del número complejo en el que i se conoce como iota y b es un número real. El valor de i es √(-1). O dicho de otro modo, un número complejo es una combinación de números reales e imaginarios. Por ejemplo, 5+11i, 10+20i, etc.
- Número real: Un número real es un número que está presente en el sistema numérico que puede ser positivo, negativo, entero, irracional racional, etc. Por ejemplo, 23, -3, 3/6.
- Número imaginario: Los números imaginarios son aquellos números que no son números reales. Por ejemplo, √3, √11, etc.
- Número complejo cero: Un número complejo cero es un número que tiene sus partes real e imaginaria ambas iguales a cero. Por ejemplo, 0+0i.
Representación gráfica del número complejo:
La representación gráfica del número complejo es como se muestra en la siguiente imagen:

Aquí, la parte real del número complejo se representa en el eje horizontal, mientras que la parte imaginaria del número complejo se representa en el eje vertical.
Valor absoluto
El valor absoluto (Módulo) de un número es la distancia del número desde cero. El valor absoluto siempre se representa en el módulo (|z|) y su valor siempre es positivo. Entonces, el valor absoluto del número complejo Z = a + ib es
|z| = √ (un 2 + segundo 2 )
Entonces, el valor absoluto del número complejo es la raíz cuadrada positiva de la suma del cuadrado de la parte real y el cuadrado de la parte imaginaria, es decir,
Prueba:
Consideremos que la moda del número complejo z se extiende de 0 a z y la moda de a, b números reales se extiende de a a 0 y b a 0. Entonces, estos valores crean un triángulo rectángulo en el que 0 es el vértice del ángulo agudo
Entonces, usando el teorema de Pitágoras, obtenemos,
|z| 2 = |a| 2 + |b| 2
|z| = √ un 2 + segundo 2
Ahora bien, en los conjuntos de números complejos z 1 > z 2 o z 1 < z 2 no tiene significado sino |z 1 | > |z 2 | o |z 1 |< |z 2 | tiene significado porque |z 1 | y |z 2 | es un número real.
Propiedades del módulo de un número complejo:
- |z| = 0 <=> z = 0i, es decir, Re(z) = 0 e Im(z) = 0
- |z| = |
 | = |-z|
| = |-z| - -|z| ≤ Re(z) ≤ |z|, -|z| ≤ Im(z) ≤ |z|
- z.
 = |z 2 |
= |z 2 | - |z 1 z 2 | = |z 1 ||z 2 |
- |z 1 / z 2 | = |z 1 |/|z 2 |
- |z 1 + z 2 | 2 = |z 1 | + |z 2 | + 2Re(z 1
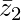 )
) - |z 1 – z 2 | 2 = |z 1 | + |z 2 | – 2Re(z 1
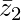 )
) - |z 1 + z 2 | 2 ≤ |z 1 | + |z 2 |
- |z 1 – z 2 | 2 ≥ |z 1 | – |z 2 |
- |az 1 – bz 2 | 2 + |bz 1 + az 2 | 2 = (a 2 + b 2 )(|z 1 | 2 + |z 2 | 2 ) O |z 1 – z 2 | 2 + |z 1 + z 2 | 2 = 2(|z 1 | 2 + |z 2 | 2 )
- |z n | = |z| norte
- 1/z = a – ib/a 2 + b 2 =
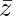 /|z| 2
/|z| 2
Ejemplo:
(yo) z = 3 + 4i
|z| = √(3 2 + 4 2 )
= √(9 + 16)
= √25
= 5
(ii) z = 5 + 6i
|z| = √(5 2 + 6 2 )
= √(25+ 36)
= √61
Ángulo de números complejos
El ángulo de un número complejo o argumento del número complejo es el ángulo inclinado desde el eje real en la dirección del número complejo que representa sobre el plano complejo o plano argand.
= bronceado -1 (b/a)
o
arg(Z) = bronceado -1 (b/a)
Aquí, Z = a + ib

Propiedades del ángel o argumento de un número complejo:
- arg(Z n ) = n arg(Z)
- argumento (Z 1 / Z 2 ) = argumento (Z 1 ) – argumento (Z 2 )
- argumento (Z 1 Z 2 ) = argumento (Z 1 ) + argumento (Z 2 )
Ejemplos:
(yo) z = 2 + 2i
= bronceado -1 (2/2)
= bronceado -1 (1)
= 45°
(ii) z = -4 + 4i
= bronceado -1 (4/-4)
= bronceado -1 (-1)
= -45°
Es importante notar aquí que el ángulo =-45° está en el 4º cuadrante,
mientras que siempre medimos el ángulo con el eje x positivo.
Entonces, tendremos que sumar 180° a la respuesta para obtener el ángulo opuesto real.
Entonces, = 180° + (-45°)
= 135°
Entonces, el número complejo anterior formará un ángulo de 135° con el eje x positivo.
Forma polar del número complejo
La forma polar de número complejo también es una forma de representar un número complejo. Generalmente, representamos un número complejo como Z = a + ib, pero en forma polar, el número complejo se representa en la combinación de módulo y argumento. Aquí, el módulo del número complejo se conoce como el valor absoluto del número complejo y el argumento se conoce como el ángulo del número complejo.
Z = r(cos θ + isen θ)
Prueba:
Consideremos que tenemos un número complejo Z = a+ib. Entonces dibujamos un plano de Argand, es un plano donde podemos representar números complejos, también se conoce como un plano complejo. En el plano de Argand, la línea horizontal representa el eje real y la línea vertical representa el eje imaginario. Ahora graficamos a en el eje real y b en el eje imaginario. Ahora representamos el vector Z como un vector de posición que comienza en 0 y la punta está en la coordenada (a, b). Supongamos que el ángulo formado por Z sobre el eje real y la distancia entre 0 y Z es r (también se conoce como la magnitud/valor absoluto del vector Z). Aquí, el par (r, ) se conoce como las coordenadas polares de Z.

De acuerdo con el diagrama, tenemos un triángulo rectángulo
Entonces, usando el teorema de Pitágoras, obtenemos,
r = |z| 2 = |a| 2 + |b| 2
r = |z| = √ un 2 + segundo 2
módulo
Ahora encontramos el valor de
bronceado -1
Número complejo:
Entonces, usando la fórmula trigonométrica, obtenemos
cos θ = a/r
Ahora multiplicamos ambos lados por r y obtenemos
r cos θ = a
sen θ = b/r
Ahora multiplicamos ambos lados por r y obtenemos
rsen θ = segundo
Entonces, obtenemos
Z = rcos θ + irsen θ
Z = r(cos θ + isen θ)
Aquí, r es el valor absoluto del número complejo y θ es el argumento del número complejo.
La forma exponencial de los números complejos:
La forma exponencial de números complejos utiliza las proporciones trigonométricas de seno y coseno para definir el exponencial complejo como un plano giratorio en forma exponencial. La forma exponencial de un número complejo generalmente viene dada por la Identidad de Euler, llamada así por el famoso matemático Leonhard Euler. Se da de la siguiente manera:
Z = re iθ
Ejemplo:
(i) Dado que r = 5 y θ = 45°. Encuentra la forma polar del número complejo
z = rcosA + (rsinA)i
z = 5cos45° + (5sen45°)i
= 5(1/√2) + (5 (1/√2))i
= 5/√2 + (5/√2)i
(ii) Dado que r = 6 y θ = 30°. Encuentra la forma polar del número complejo
z = rcosA + (rsinA)i
z = 6cos30° + (6sen30°)i
= 6(√3/2) + (6(1/2))yo
= 3√3 + 3i
Convierte forma rectangular a forma polar:
Analicemos este concepto con la ayuda de un ejemplo:
Supongamos que tenemos un número complejo, es decir, Z = 3 + 4i
Tiene forma rectangular, así que ahora tenemos que convertirlo a forma polar.
Paso 1: Entonces, primero calcularemos el módulo de los números complejos y luego el ángulo.
|Z|= √(3 2 + 4 2 )
= √(9 + 16)
= √25
= 5
Paso 2: Ahora encontramos el ángulo del número complejo,
θ = tan -1 (y/x)
= bronceado -1 (4/3)
= 53,1°
Paso 3: Como sabemos que la fórmula de la forma polar es:
Z = r(cos θ + isen θ)
Ahora pon el valor de r y θ en esta ecuación, obtenemos
Z = 5(cos 53.1 + isen 53.1)
Por tanto, la forma polar de 3 + 4i es 5(cos 53.1 + isen 53.1)
Problemas de muestra
Pregunta 1. Encuentra el valor absoluto de z = 4 + 8i
Solución:
El número complejo dado es z = 4 + 8i
Como sabemos que la fórmula del valor absoluto es
|z| = √ (un 2 + segundo 2 )
Entonces, a = 4 y b = 8, obtenemos
|z| = √(4 2 + 8 2 )
|z| = √80
Pregunta 2. Encuentra el valor absoluto de z = 2 + 4i
Solución:
El número complejo dado es z = 2 + 4i
Como sabemos que la fórmula del valor absoluto es
|z| = √ (un 2 + segundo 2 )
Entonces, a = 2 y b = 4, obtenemos
|z| = √(2 2 + 4 2 )
|z| = √20
Pregunta 3. Encuentra el ángulo del número complejo: z = √3 + i
Solución:
El número complejo dado es z = √3 + i
Como sabemos, que
= bronceado -1 (b/a)
Entonces, a = √3 y b = 1, obtenemos
= bronceado -1 (1/ √3 )
= 30°
Pregunta 4. Encuentra el ángulo del número complejo: z = 6 + 6i
Solución:
El número complejo dado es z = 6 + 6i
Como sabemos, que
= bronceado -1 (b/a)
Entonces, a = 6 y b = 6, obtenemos
= bronceado -1 (6/6)
= 45°
Pregunta 5. Convierte z = 5 + 5i en forma polar
Solución:
El número complejo dado es z = 5 + 5i
Como sabemos que
Z = r(cos θ + isen θ) …(1)
Ahora encontramos el valor de r
r = √(5 2 + 5 2 )
r = √(25 + 25)
r = √50
Ahora encontramos el valor de θ
= bronceado -1 (5/5)
= bronceado -1 (1)
= 45°
Ahora ponga todos estos valores en la ecuación (1), obtenemos
Z = √50(cos 45° + isen 45°)
Pregunta 6. Convierte z = 2 + √3i en forma polar
Solución:
El número complejo dado es z = 2 + 2√3i
Como sabemos que
Z = r(cos θ + isen θ) …(1)
Ahora encontramos el valor de r
r = √(2 2 + (2√3) 2 )
r = √(4 + 12)
r = √16
r = 4
Ahora encontramos el valor de θ
= bronceado -1 (2√3/2)
= bronceado -1 (√3)
= 60°
Ahora ponga todos estos valores en la ecuación (1), obtenemos
Z = 4(cos 60° + isen 60°)
Publicación traducida automáticamente
Artículo escrito por neeraj kumar 13 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA