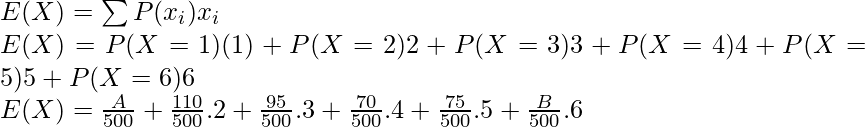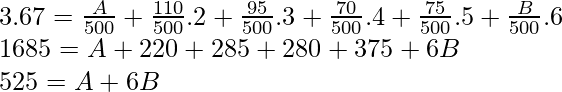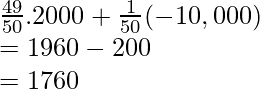Valor esperado

Las variables aleatorias son las funciones que asignan una probabilidad a algunos resultados en el espacio muestral. Son muy útiles en el análisis de experimentos aleatorios de la vida real que se vuelven complejos. Estas variables toman algunos resultados de un espacio muestral como entrada y le asignan algunos números reales. La expectativa es una parte importante del análisis de variables aleatorias. Da la salida promedio de la variable aleatoria. Intuitivamente quiere decir que da el valor que la variable aleatoria va a arrojar con mayor frecuencia cuando se repite el experimento una infinidad de veces.

Variables aleatorias y expectativas

Los experimentos aleatorios son aquellos experimentos en los que no es posible estar seguro de los resultados. En tales casos, solo es posible asignar probabilidades a los resultados. Las variables aleatorias conectan los resultados con un cierto número real. Por ejemplo, considere el experimento de lanzar una moneda tres veces. Lo que hay que tener en cuenta es que se puede definir una variable aleatoria de acuerdo con nuestras necesidades, pero la única condición es que cada resultado del espacio muestral debe recibir un valor de una variable aleatoria.

Entonces, en este caso, sea R la variable aleatoria, y en este caso, se define como,

R = Número de cabezas

Espacio de muestra = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

El valor dado por R para cada resultado se muestra a continuación en la tabla.

Aporte	Producción
R(HHH)	3
R(HH)	2
R(HTH)	2
R(HTT)	1
R(THH)	2
R(THT)	1
R(TTH)	1
R(TTT)	0

Observe que la variable aleatoria puede asignar más de un resultado a un solo valor.

Expectativa

Para una variable aleatoria X, la expectativa da una idea del valor promedio que obtiene X cuando el experimento se repite muchas veces. Ya que este valor se mapea con un resultado en el espacio muestral. El valor esperado se puede usar para determinar cuál de los resultados es más probable que suceda cuando el experimento se repite muchas veces.

Para la variable aleatoria X que asume valores x ₁ , x ₂ , x ₃ ,…x _n con probabilidad P(x ₁ ), P(x ₂ ), P(x ₃ ), … P(x _n )

La expectativa de X se define como,

E(x) = $\sum P(x_{i})x_{i}$

Las expectativas tienen muchos casos de uso y aplicaciones en la vida real. Estos conceptos son utilizados por las compañías de seguros para calcular la probabilidad de muerte de una persona. Las expectativas también se utilizan en los juegos de azar. Por ejemplo, mientras juega al póquer, o tal vez analizando un sistema de lotería. Los analistas lo utilizan para calcular la probabilidad de ganar. Este concepto también se usa mucho en el campo de la Inteligencia Artificial (IA) para comprender escenarios y acciones de la vida real.

Seguro de Vida a Término y Probabilidad de Muerte

Considere un ejemplo, digamos que Akhil tiene dos hijos y una esposa, y quiere tomar una póliza de seguro para sí mismo para que, en caso de cualquier deformidad, su familia no tenga que sufrir económicamente. Compra una póliza de seguro de 50 lakh de rupias. La póliza es válida durante los próximos 20 años, lo que significa que si algo le sucede a Akhil en los próximos 10 años, la empresa pagará a su familia 50 lakhs de rupias. Este tipo de pólizas se denominan pólizas de seguro de vida a largo plazo. La condición de esta póliza es que Akhil tendrá que pagar una prima de 50.000 rupias al año.

¿Cómo obtienen ganancias las empresas y calculan la probabilidad de muerte en estos casos?

Importe total pagado por Akhil en 10 años = 50.000 rupias × 10

= 5.00.000 rupias

Póliza de seguro = 50,00,000

La relación se convierte en $\frac{5,00,000}{50,00,000} = \frac{1}{10}$ . Esto significa que por Rs 10 de seguro obtienen una prima de Rs 1. Dado que están tratando de obtener ganancias, necesitan obtener al menos 10 Akhils para alcanzar el punto de equilibrio. En ese caso, de cada 10, si solo muere un Akhil, la empresa puede alcanzar el punto de equilibrio.

Entonces, si hay una probabilidad de $\frac{1}{10}$ que un candidato muera y la compañía tiene 10 asegurados, no habrá pérdida ni ganancia. Por lo tanto, para obtener una ganancia

P (Akhil muriendo) ≤ 0.1

Obtener datos del valor esperado

El valor esperado da el valor central de la variable aleatoria. Aquí es donde se encuentran la mayoría de los resultados de las variables aleatorias cuando los experimentos se repiten muchas veces. Estos valores son útiles al inferir las otras variables que faltan la mayor parte del tiempo al realizar tales experimentos aleatorios. Los datos se pueden recuperar mediante manipulaciones y expresiones algebraicas básicas para calcular el valor esperado. El ejemplo dado a continuación aclarará aún más este método.

Ejemplo: el papá de Aman le dio un dado. Para comprobar si era un dado justo, hizo rodar el dado 500 veces y anotó las frecuencias de los valores obtenidos en la tabla en una hoja de papel. Debido a la lluvia, algunos valores sobre la mesa fueron arrastrados. Entonces, en lugar de hacer todos los experimentos nuevamente, lanzó el dado 20 veces y concluyó que el valor esperado en 20 lanzamientos era 3.37. La tabla de lavado se da a continuación. Encuentre los valores de las frecuencias que faltan.

Valor del dado	Frecuencia absoluta
1	A
2	110
3	95
4	70
5	75
6	B
Total	500

Solución:

Suponiendo que el valor esperado sigue siendo el mismo tanto en 20 como en 500 ensayos.

Digamos que la variable aleatoria “X” se define como el valor obtenido en el dado.

X puede tomar valores como 1, 2, 3, 4, 5 y 6

El valor esperado de una variable aleatoria viene dado por,

E(x) = $\sum P(x_{i})x_{i}$

$E(X) = \sum P(x_{i})x_{i} \\ E(X) = P(X = 1)(1) + P(X = 2)2 + P(X = 3)3 + P(X = 4)4 + P(X = 5)5 + P(X = 6)6 \\ E(X) = \frac{A}{500} + \frac{110}{500}.2 + \frac{95}{500}.3 + \frac{70}{500}.4 + \frac{75}{500}.5 + \frac{B}{500}.6 \\$

Sustituyendo el valor esperado,

$3.67 = \frac{A}{500} + \frac{110}{500}.2 + \frac{95}{500}.3 + \frac{70}{500}.4 + \frac{75}{500}.5 + \frac{B}{500}.6 \\ 1685 = A + 220 + 285 + 280 + 375 + 6B \\ 525 = A + 6B$

Ahora esta ecuación tiene dos variables, se requiere una ecuación más para resolver esto.

A + 110 + 95 + 70 + 75 + B = 500

⇒ A+ B = 150

Entonces, las dos ecuaciones son,

A + B = 150

A + 6B = 525

Resolviendo estas ecuaciones, los valores de las variables resultan ser.

A = 75 y B = 75.

Ganancia esperada del billete de lotería

Las expectativas se pueden utilizar para analizar las ganancias que se pueden obtener de un billete de lotería. En tales juegos, las posibilidades de ganar son pocas y los jugadores generalmente terminan perdiendo dinero. A través de la teoría de la probabilidad y las expectativas, se pueden calcular las posibilidades y las ganancias esperadas utilizando las decisiones más sabias que se pueden tomar al jugar tales juegos.

Ejemplo: Asif está jugando a la lotería en la que tiene que elegir dos números. Si el boleto coincide con ambos números, ganará el gran premio, que es Rs10005. Si solo un número coincide, ganará un pequeño premio de 1005 rupias y el costo de un boleto de lotería es de 5 rupias. Halle la ganancia esperada del boleto de lotería.

Solución :

Supongamos que Asif saca un billete de lotería «04». Sea X la variable aleatoria que representa la ganancia cuando se extrajo el boleto “04”.

E(X) = P(ganar el premio mayor)(10005 – 5) + P(ganar el premio pequeño)(1005 – 5) + P(no ganar nada)(-5)

Ahora, se requieren los valores de estas probabilidades.

P(ganar el gran premio) = Ambos números coinciden

= $\frac{1}{10}.\frac{1}{10} = \frac{1}{100}$

P(ganar un pequeño premio) = Solo uno de los números coincide

= $2.\frac{1}{10}.\frac{9}{10} = \frac{18}{100}$

P(ganar ninguno de estos premios) = Ninguno de los números coincide

= $\frac{9}{10}.\frac{9}{10} = \frac{81}{100}$

Sustituyendo estos valores,

E(X) = P(ganar el premio mayor)(10005 – 5) + P(ganar el premio pequeño)(1005 – 5) + P(no ganar nada)(-5)

⇒ E(X) = $\frac{1}{100}.10000 + \frac{18}{100}.1000 + \frac{81}{100}.(-5)$

⇒ E(X) = 100 + 180 – 4,05

⇒E(X) = 275,95

Valor esperado durante la pesca

Este es otro ejemplo más del caso de uso del valor esperado. En este caso, se trata de una apuesta entre dos amigos que van a pescar. Incluso antes de pescar, las posibilidades o los márgenes de ganancia pueden analizarse utilizando las expectativas de variables aleatorias. El siguiente ejemplo muestra uno de esos incidentes de apuestas entre dos amigos que fueron a pescar y apostaron por el pescado.

Ejemplo: Dos amigos están pescando en un estanque que contiene 10 truchas y 10 peces luna. Cada vez que pescan un pez, lo sueltan de inmediato. Hicieron una apuesta. Si los próximos tres peces que captura el amigo A son todos peces luna, entonces el amigo B le pagará 100 rupias; de lo contrario , el amigo A tendrá que pagar 20 rupias a B. Halle la ganancia esperada de la apuesta.

Solución:

Sea X una variable aleatoria que denota el beneficio de la apuesta.

E(X) = P(A atrapa los tres peces luna)(100) + P(A no puede atrapar los tres peces luna)(-20)

Calculando las probabilidades,

P(A atrapa los tres peces luna) = $\frac{10}{20}.\frac{10}{20}.\frac{10}{20} = \frac{1}{8}$

P(A no atrapa los tres peces luna) = 1 – P(A atrapa los tres peces luna)

= 1 – $\frac{1}{8}$

= $\frac{7}{8}$

Sustituyendo los valores calculados arriba en la ecuación de expectativa,

E(X) = P(A atrapa los tres peces luna)(100) + P(A no puede atrapar los tres peces luna)(-20)

⇒ E(X) = P(A atrapa los tres peces luna)(100) + P(A no puede atrapar los tres peces luna)(-20)

⇒ E(X) = $\frac{1}{8}.100 + \frac{7}{8}.(-20)$

⇒ E(X) = $\frac{-40}{8} = -5$

Comparación del seguro con el valor esperado

Las compañías de seguros muestran muchos planes y tratan de atraer a los clientes para que los compren. No todos los planes son beneficiosos para los clientes. Uno de esos casos es el seguro médico. Muchas compañías de seguros, para obtener más ganancias, crean esquemas atractivos que en realidad no son beneficiosos a largo plazo. En tales casos, se vuelve esencial utilizar las expectativas y calcular los costos médicos esperados. Dichos métodos generalmente ayudan a diferenciar entre planes y tomar una decisión acertada sobre el seguro médico. Para tener una mejor idea de este caso, consideremos el siguiente ejemplo.

Ejemplo: Vasu quiere comprar un plan de seguro médico, pero está confundido entre el plan A y el plan B.

Plan A: este es un plan de deducible bajo, tendrá que pagar las primeras 10,000 rupias de cualquier costo médico. Además , para cubrir el plan, tendrá que pagar 80.000 rupias al año.

Plan B: este es un plan de deducible alto, tendrá que pagar las primeras 25,000 rupias de cualquier costo médico. Además, para cubrir el plan, tendrá que pagar 60.000 rupias al año.

Encuentre el costo esperado para ambos planes y ayude a Vasu a decidir. Se da una tabla que da las estadísticas sobre la probabilidad de estos gastos médicos.

Costo Médico	Probabilidad
$0	30 %
10000 rupias	25 %
40.000 rupias	20 %
70.000 rupias	20 %
1,50,000 rupias	5 %

Solución:

Deje que la variable aleatoria X defina el costo esperado,

Valor esperado para el Plan A:

E(X) = 80.000 + 0 (0,3) + 10000(0,25) + 10000(0,2) + 10000(0,2) + 10000(0,05)

⇒ E(X) = 80 000 + 2500 + 2000 + 2000 + 500

⇒ E(X) = 87000

Valor esperado para el plan B:

E(X) = 60.000 + 0 (0,3) + 10000(0,25) + 25000(0,2) + 25000(0,2) + 25000(0,05)

⇒ E(X) = 80 000 + 2500 + 5000 + 5000 + 12500

⇒ E(X) = 1,05,000

La mayoría de los gastos esperados están en el plan B. Por lo tanto, Vasu debería tomar el plan A.

Veamos algunos problemas sobre estos conceptos.

Problemas de muestra

Pregunta 1: Encuentra el valor esperado del resultado cuando se lanza un dado.

Solución:

Considere que X es una variable aleatoria que representa el valor que surge cuando se lanza un dado.

X = {1, 2, 3, 4, 5, 6}

Ahora, dado que el dado es justo, la probabilidad de obtener cada resultado es igual. Eso es $\frac{1}{6}$

E(X) = $\sum x_{i}P(X = x_i)$

⇒ E(X) = P(X = 1)(1) + P(X = 2)(2) + P(X = 3)(3) + P(X = 4)(4) + P(X = 5)(5) + P(X = 6)(6)

⇒ E(X) = $\frac{1}{6}(1 + 2 + 3 + 4 + 5 + 6)$

⇒ E(X) = 3

Pregunta 2: Una empresa fabrica teléfonos. De 100 teléfonos, uno está defectuoso. Por cada teléfono, la empresa obtiene una ganancia de 2.000 rupias y una pérdida de 10.000 rupias por el teléfono defectuoso. Encuentre la ganancia esperada.

Solución:

Sea X el beneficio esperado

E() = $\sum x_{i}P(X = x_i)$

⇒ E(X) = P(X = El teléfono funciona)(2000) + P(X = Teléfono defectuoso)(10 000)

⇒ E(X) = $\frac{49}{50}.2000 + \frac{1}{50}(-10,000) \\ = 1960 -200 \\ = 1760$

⇒ E(X) = 1760

Pregunta 3: En un experimento de lanzamiento de moneda tres veces. Encuentre el número esperado de cabezas.

Solución:

Sea X el número de caras obtenidas

Espacio de muestra = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

E() = $\sum x_{i}P(X = x_i)$

⇒ E(X) =P(X = 0)(0) + P(X = 1)(1) + P(X =2)(2) + P(X = 3)(3)

Descubriendo las probabilidades,

P(X = 0) = $\frac{1}{8}$

P(X = 1) = $\frac{3}{8}$

P(X = 2) = $\frac{3}{8}$

P(X = 3) = $\frac{1}{8}$

⇒ E(X) = P(X = 0)(0) + P(X = 1)(1) + P(X =2)(2) + P(X = 3)(3)

⇒ E(X) = $\frac{1}{8}. 0 + \frac{3}{8}.1 + \frac{3}{8}.2 + \frac{1}{8}.3$

⇒ E(X) = $\frac{12}{8}$

⇒ E(X) = 1,5

Pregunta 4: Dos amigos están pescando en un estanque que contiene 5 truchas y 5 peces luna. Cada vez que pescan un pez, lo sueltan de inmediato. Hicieron una apuesta. Si los próximos tres peces que captura el amigo A son todos peces luna, entonces el amigo B le pagará 10 rupias; de lo contrario , el amigo A tendrá que pagar 2 rupias a B. Halle la ganancia esperada de la apuesta.

Solución:

Sea X una variable aleatoria que denota el beneficio de la apuesta.

E(X) = P(A atrapa los tres peces luna)(10) + P(A no puede atrapar los tres peces luna)(-2)

Calculando las probabilidades,

P(A atrapa los tres peces luna) = $\frac{5}{10}.\frac{5}{10}.\frac{5}{10} = \frac{1}{8}$

P(A no atrapa los tres peces luna) = 1 – P(A atrapa los tres peces luna)

= 1 – $\frac{1}{8}$

= $\frac{7}{8}$

Sustituyendo los valores calculados arriba en la ecuación de expectativa,

E(X) = P(A atrapa los tres peces luna)(10) + P(A no puede atrapar los tres peces luna)(-2)

⇒ E(X) = P(A atrapa los tres peces luna)(10) + P(A no puede atrapar los tres peces luna)(-2)

⇒ E(X) = $\frac{1}{8}.10 + \frac{7}{8}.(-2)$

⇒ E(X) = $\frac{-4}{8} = -\frac{1}{2}$

Pregunta 5: Encuentra el valor esperado del resultado cuando se lanza un dado. Dado que el dado no es justo, la probabilidad de sacar un 6 es de 0,4 y el resto de números son igualmente probables.

Solución:

Considere que X es una variable aleatoria que representa el valor que surge cuando se lanza un dado.

X = {1, 2, 3, 4, 5, 6}

Ahora bien, como el dado no es justo morir,

P(6) = 0,4

P(1) = P(2) = P(3) = P(4) = P(5) = 0,12

E(X) = $\sum x_{i}P(X = x_i)$

⇒ E(X) = P(X = 1)(1) + P(X = 2)(2) + P(X = 3)(3) + P(X = 4)(4) + P(X = 5)(5) + P(X = 6)(6)

⇒ E(X) = (0,12)(1) + (0,12)(2) + (0,12)(3) + (0,12)(4) + (0,12)(5) + (0,4)(6)

⇒ E(X) = (0,12)(1 + 2 + 3+ 4+ 5) + 2,4

⇒ E(X) = 1,8 + 2,4

⇒E(X) = 4,2

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Variables aleatorias y expectativas

Valor esperado

Problemas de muestra

Deja una respuesta Cancelar la respuesta