Vectorización de descenso de gradiente

En Machine Learning, los problemas de regresión se pueden resolver de las siguientes maneras:

1. Uso de algoritmos de optimización : descenso de gradiente

Descenso de gradiente por lotes.
Descenso de gradiente estocástico.
Descenso de gradiente de mini lotes
Otros algoritmos de optimización avanzada como (descenso conjugado…)

2. Usando la ecuación normal :

Usando el concepto de Álgebra Lineal.

Consideremos el caso del descenso de gradiente por lotes para el problema de regresión lineal univariante.

La función de costo para este problema de regresión es:

$J(\Theta)=(1/2m)*\sum_{i=1}^m(h_{\theta}(x^i)-y^i)^2$

Meta:

$minimize_{\ \theta_{o},\theta_{1}}\ \ J({\theta})$

Para resolver este problema, podemos optar por un enfoque vectorizado (usando el concepto de álgebra lineal) o un enfoque no vectorizado (usando for-loop).

1. Enfoque no vectorizado:

Aquí, para resolver las expresiones matemáticas mencionadas a continuación, usamos for loop .

The above mathematical expression is a part of Cost Function.

$\sum_{i=1}^m(h_{\theta}(x^i)-y^i)^2$

The above Mathematical Expression is the hypothesis.

$h_{\theta}=\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+... +\theta_{n}x_{n}\\ where,\\ h_{\theta}=hypothesis.\\$

Código: Implementación de Python de Graduado no vectorizado

# Import required modules.
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
import numpy as np
import time
   
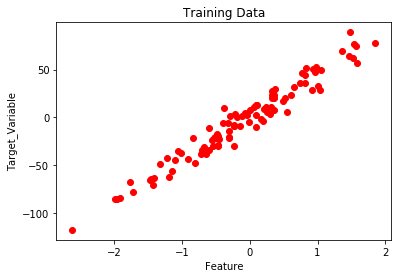
# Create and plot the data set.
x, y = make_regression(n_samples = 100, n_features = 1,
                       n_informative = 1, noise = 10, random_state = 42)
  
plt.scatter(x, y, c = 'red')
plt.xlabel('Feature')
plt.ylabel('Target_Variable')
plt.title('Training Data')
plt.show()
  
# Convert y from 1d to 2d array.
y = y.reshape(100, 1)
   
# Number of Iterations for Gradient Descent
num_iter = 1000
   
# Learning Rate
alpha = 0.01
   
# Number of Training samples.
m = len(x)
   
# Initializing Theta.
theta = np.zeros((2, 1),dtype = float)
   
# Variables
t0 = t1 = 0
Grad0 = Grad1 = 0
  
# Batch Gradient Descent.
start_time = time.time()
   
for i in range(num_iter):
    # To find Gradient 0.
    for j in range(m):
        Grad0 = Grad0 + (theta[0] + theta[1] * x[j]) - (y[j])
      
    # To find Gradient 1.
    for k in range(m):
        Grad1 = Grad1 + ((theta[0] + theta[1] * x[k]) - (y[k])) * x[k]
    t0 = theta[0] - (alpha * (1/m) * Grad0)
    t1 = theta[1] - (alpha * (1/m) * Grad1)
    theta[0] = t0
    theta[1] = t1
    Grad0 = Grad1 = 0
       
# Print the model parameters.    
print('model parameters:',theta,sep = '\n')
   
# Print Time Take for Gradient Descent to Run.
print('Time Taken For Gradient Descent in Sec:',time.time()- start_time)
  
# Prediction on the same training set.
h = []
for i in range(m):
    h.append(theta[0] + theta[1] * x[i])
       
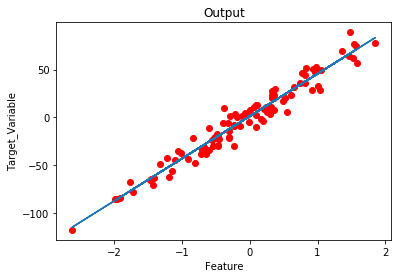
# Plot the output.
plt.plot(x,h)
plt.scatter(x,y,c = 'red')
plt.xlabel('Feature')
plt.ylabel('Target_Variable')
plt.title('Output')

Producción:

model parameters:
[[ 1.15857049]
 [44.42210912]]
 
Time Taken For Gradient Descent in Sec: 2.482538938522339

2. Enfoque vectorizado:

Aquí para resolver las expresiones matemáticas mencionadas a continuación, usamos Matrix y Vectores (Álgebra Lineal).

The above mathematical expression is a part of Cost Function.

$\sum_{i=1}^m(h_{\theta}(x^i)-y^i)^2$

The above Mathematical Expression is the hypothesis.

$h_{\theta}=\theta^T.X\\ where,\\ h_{\theta}=hypothesis.\\ \theta= \begin{bmatrix} \theta_{0} \\ \theta_{1}\\ \theta_{2}\\ \theta_{3}\\ .\\ .\\ \theta_{n}\\ \end{bmatrix} X= \begin{bmatrix} {x_{0}} \\ {x_{1}}\\ {x_{2}}\\ {x_{3}}\\ .\\ .\\ {x_{n}}\\ \end{bmatrix}\\$

Descenso de gradiente por lotes:

$Loop\ until\ converge\{\\ \ \theta_{j}:=\theta_{j}-(1/m)*(\alpha)*\frac{\partial J(\theta)}{\partial \theta_{j}} \\ \}\\ Let, \ Gradients=\frac{\partial J(\theta)}{\partial \theta_{j}}$

Concepto para encontrar gradientes usando operaciones matriciales:

$X\_New= \begin{bmatrix} {x_{0}^1} & {x_{1}^1} \\ {x_{0}^2} & {x_{1}^2}\\ {x_{0}^3} & {x_{1}^3}\\ {x_{0}^4} & {x_{1}^4}\\ . & .\\ . & .\\ . & .\\ {x_{0}^m} & {x_{1}^m} \end{bmatrix}_{m X 2} \theta= \begin{bmatrix} \theta_{0} \\ \theta_{1}\\ \end{bmatrix}_{2X1}\\ where,\\ \x_{0}^i=1\\$

$H(\theta)=X\_New\ .\ \theta\\ H(\theta)= \begin{bmatrix} {\Theta_{0}}{x_{0}^1}+{\Theta_{1}}{x_{1}^1} \\ {\Theta_{0}}{x_{0}^2}+{\Theta_{1}}{x_{1}^2}\\ {\Theta_{0}}{x_{0}^3}+{\Theta_{1}}{x_{1}^3}\\ {\Theta_{0}}{x_{0}^4}+{\Theta_{1}}{x_{1}^4}\\ .\\ .\\ . \\ {\Theta_{0}}{x_{0}^m}+{\Theta_{1}}{x_{1}^m} \end{bmatrix}_{mX1} And\ \ \ Y= \begin{bmatrix} {y^1}\\ {y^2}\\ {y^3}\\ .\\ .\\ .\\ {y^m} \end{bmatrix}_{mX1}\\$

$H(\theta)-Y= \begin{bmatrix} {\Theta_{0}}{x_{0}^1}+{\Theta_{1}}{x_{1}^1} -y^1\\ {\Theta_{0}}{x_{0}^2}+{\Theta_{1}}{x_{1}^2}-y^2\\ {\Theta_{0}}{x_{0}^3}+{\Theta_{1}}{x_{1}^3}-y^3\\ {\Theta_{0}}{x_{0}^4}+{\Theta_{1}}{x_{1}^4}-y^4\\ .\\ .\\ . \\ {\Theta_{0}}{x_{0}^m}+{\Theta_{1}}{x_{1}^m}-y^m \end{bmatrix}_{mX1} \\$

$X\_New^T= \begin{bmatrix} {x_{0}^1\ x_{0}^2\ x_{0}^3\ .\ .\ .\ x_{0}^m}\\ {x_{1}^1\ x_{1}^2\ x_{1}^3\ .\ .\ .\ x_{1}^m} \end{bmatrix}_{2Xm} \\$

$Gradients=X\_New\ . \ (H(\theta)-Y)\\ = \begin{bmatrix} {x_{0}^1(\Theta x_{0}^1+\Theta x_{1}^1-y^1)\ + \ x_{0}^2(\Theta x_{0}^2+\Theta x_{1}^2-y^2)\ + \ x_{0}^3(\Theta x_{0}^3+\Theta x_{1}^3-y^3)\ + . . .}\\ {x_{1}^1(\Theta x_{0}^1+\Theta x_{1}^1-y^1)\ + \ x_{1}^2(\Theta x_{0}^2+\Theta x_{1}^2-y^2)\ + \ x_{1}^3(\Theta x_{0}^3+\Theta x_{1}^3-y^3)\ + . . .}\\ \end{bmatrix}_{2X1}\\$

$Finally\ we\ can \ say,\\ \ \ \ Gradients=\frac{\partial J(\theta)}{\partial \theta_{j}}=X\_New^T.(X\_New.\theta-Y)$

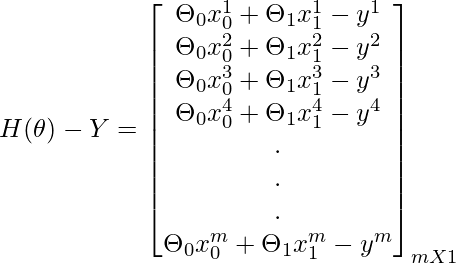
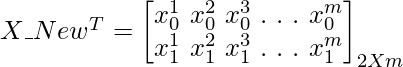
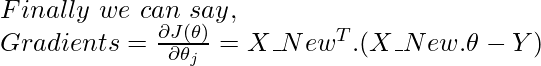
Código: implementación de Python del enfoque de descenso de gradiente vectorizado

# Import required modules.
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
import numpy as np
import time
   
# Create and plot the data set.
x, y = make_regression(n_samples = 100, n_features = 1,
                       n_informative = 1, noise = 10, random_state = 42)
  
plt.scatter(x, y, c = 'red')
plt.xlabel('Feature')
plt.ylabel('Target_Variable')
plt.title('Training Data')
plt.show()
  
  
# Adding x0=1 column to x array.
X_New = np.array([np.ones(len(x)), x.flatten()]).T
  
# Convert y from 1d to 2d array.
y = y.reshape(100, 1)
   
# Number of Iterations for Gradient Descent
num_iter = 1000
   
# Learning Rate
alpha = 0.01
   
# Number of Training samples.
m = len(x)
   
# Initializing Theta.
theta = np.zeros((2, 1),dtype = float)
   
# Batch-Gradient Descent.
start_time = time.time()
   
for i in range(num_iter):
    gradients = X_New.T.dot(X_New.dot(theta)- y)
    theta = theta - (1/m) * alpha * gradients
   
# Print the model parameters.    
print('model parameters:',theta,sep = '\n')
   
# Print Time Take for Gradient Descent to Run.
print('Time Taken For Gradient Descent in Sec:',time.time() - start_time)
  
# Hypothesis.
h = X_New.dot(theta) # Prediction on training data itself.
   
# Plot the Output.
plt.scatter(x, y, c = 'red')
plt.plot(x ,h)
plt.xlabel('Feature')
plt.ylabel('Target_Variable')
plt.title('Output')

Producción:

model parameters:
[[ 1.15857049]
 [44.42210912]]
 
Time Taken For Gradient Descent in Sec: 0.019551515579223633

Observaciones:

La implementación de un enfoque vectorizado disminuye el tiempo necesario para la ejecución de Gradient Descent (Código eficiente).
Fácil de depurar.

Publicación traducida automáticamente

Artículo escrito por rohan007 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA