Verifique si el Triángulo de Pascal es posible con una capa completa usando números hasta N

Dado un número N , la tarea es determinar si es posible hacer el triángulo de Pascal con una capa completa usando el número total N entero si es posible imprimir Sí de lo contrario imprimir No.

Nota: el triángulo de Pascal es una array triangular de los coeficientes binomiales. Las siguientes son las primeras 6 filas del Triángulo de Pascal. 
 

1  
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1 
1 5 10 10 5 1 

En el Triángulo de Pascal desde la capa superior hay 1 entero, en cada capa siguiente de arriba a abajo el tamaño de la capa aumenta en 1.

Ejemplos:

Entrada: N = 10
Salida: Sí
Explicación: 
Puede usar 1, 2, 3 y 4 enteros para hacer la primera, segunda, tercera y cuarta capa del triángulo de pascal respectivamente y también N = 10 satisfaga usando (1 + 2 + 3 + 4) números enteros en cada capa = 10.
Entrada: N = 5 
Salida: No
Explicación: 
puede usar 1 y 2 números enteros para hacer la primera y la segunda capa respectivamente y después de eso solo le quedan 2 números enteros y no puede hacer la tercera capa completa ya que esa capa requería 3 enteros.

Enfoque: aquí estamos usando el número entero 1, 2, 3,… en cada capa a partir de la primera capa, por lo que solo podemos completar el triángulo de Pascal si es posible representar N por la suma de 1 + 2 +…

1. La suma de los primeros X enteros viene dada por 
    

1. Solo podemos hacer el triángulo de pascal usando N enteros si y solo si 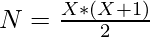 donde X debe ser un entero positivo. Así que tenemos que comprobar si existe algún valor entero positivo de x o no.
2. Para determinar el valor de X del segundo paso, podemos deducir la fórmula como: 
    

1. Si el valor de X es un número entero para el valor dado de N, entonces podemos hacer el Triángulo de Pascal. De lo contrario, no podemos hacer Pascal Triangle.

A continuación se muestra la implementación del enfoque anterior:
 

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to check if Pascaltriangle
// can be made by N integers
void checkPascaltriangle(int N)
{
    // Find X
    double x = (sqrt(8 * N + 1) - 1) / 2;
 
    // If x is integer
    if (ceil(x) - x == 0)
        cout << "Yes";
 
    else
        cout << "No";
}
 
// Driver Code
int main()
{
    // Given number N
    int N = 10;
 
    // Function Call
    checkPascaltriangle(N);
    return 0;
}

// Java program for the above approach
class GFG{
 
// Function to check if Pascaltriangle
// can be made by N integers
static void checkPascaltriangle(int N)
{
     
    // Find X
    double x = (Math.sqrt(8 * N + 1) - 1) / 2;
 
    // If x is integer
    if (Math.ceil(x) - x == 0)
        System.out.print("Yes");
    else
        System.out.print("No");
}
 
// Driver Code
public static void main(String[] args)
{
     
    // Given number N
    int N = 10;
 
    // Function call
    checkPascaltriangle(N);
}
}
 
// This code is contributed by amal kumar choubey

# Python3 program for the above approach
import math
 
# Function to check if Pascaltriangle
# can be made by N integers
def checkPascaltriangle(N):
     
    # Find X
    x = (math.sqrt(8 * N + 1) - 1) / 2
 
    # If x is integer
    if (math.ceil(x) - x == 0):
        print("Yes")
    else:
        print("No")
 
# Driver Code
 
# Given number N
N = 10
 
# Function call
checkPascaltriangle(N)
 
# This code is contributed by sanjoy_62

// C# program for the above approach
using System;
 
class GFG{
 
// Function to check if Pascaltriangle
// can be made by N integers
static void checkPascaltriangle(int N)
{
     
    // Find X
    double x = (Math.Sqrt(8 * N + 1) - 1) / 2;
 
    // If x is integer
    if (Math.Ceiling(x) - x == 0)
        Console.Write("Yes");
    else
        Console.Write("No");
}
 
// Driver Code
public static void Main(String[] args)
{
     
    // Given number N
    int N = 10;
 
    // Function call
    checkPascaltriangle(N);
}
}
 
// This code is contributed by amal kumar choubey

<script>
 
      // JavaScript program for the above approach
 
      // Function to check if Pascaltriangle
      // can be made by N integers
      function checkPascaltriangle(N) {
        // Find X
        var x = (Math.sqrt(8 * N + 1) - 1) / 2;
 
        // If x is integer
        if (Math.ceil(x) - x == 0)
        document.write("Yes");
        else
        document.write("No");
      }
 
      // Driver Code
 
      // Given number N
      var N = 10;
 
      // Function Call
      checkPascaltriangle(N);
       
    </script>

Yes

Complejidad de tiempo: O(sqrt(N)) 
Espacio auxiliar: O(1)