Winsorización

Winsorización es el proceso de reemplazar los valores extremos de los datos estadísticos para limitar el efecto de los valores atípicos en los cálculos o los resultados obtenidos al usar esos datos. El valor medio calculado después de la sustitución de los valores extremos se denomina media winsorizada.

 Por ejemplo, el 90% de winsorización significa el reemplazo del 5% superior y el 5% inferior de los datos. El 5% superior de los datos se reemplaza por el valor de los datos en el percentil 95 y el valor del 5% inferior de los datos se reemplaza por el valor de los datos en el percentil 5. 

Aporte:

• Una array numérica cuyos valores en el extremo superior y el extremo inferior se van a winsorizar.
• El primer argumento de la tupla es el porcentaje de valores en el extremo inferior que se van a winsorizar.
• El segundo argumento de la tupla es el porcentaje de valores en el extremo superior que se van a winsorizar.

Producción:

Una array numérica cuyos valores en el extremo superior y en el extremo inferior están winsorizados según lo definido por el usuario.

Ejemplo 1:

# Libraries to be imported
import numpy as np
import matplotlib.pyplot as plt
import random
from scipy.stats.mstats import winsorize

Veamos un ejemplo donde los valores atípicos están presentes tanto en el extremo superior como en el inferior de los datos.

# Creating an array with 100 random values
array = [np.random.randint(100) for i in range(100)]
  
# Creating outliers
# Here, the values which are selected for creating outliers 
# are appended so that same outliers are not created again.
AlreadySelected = []
i = 0
  
# Creating 5 outliers on the lower end
while (i < 5):
    x = np.random.choice(array)  # Randomly selecting a value from the array
    y = x - mean*3
    array = np.append(array, y)
    if (x not in already_selected):
        AlreadySelected.append(y)
  
        i += 1
  
    else:
        continue
  
# Creating 5 outliers on the upper end
i = 0
while (i < 5):
    x = np.random.choice(array)  # Randomly selecting a value from the array
    y = x + mean*4
    array = np.append(array, y)
    if (x not in already_selected):
        AlreadySelected.append(y)
  
        i += 1
  
    else:
        continue
  
std = np.std(array)  # Storing the standard deviation of the array
mean = np.mean(array)  # Storing the mean of the array
  
plt.boxplot(array)
plt.title('Array with Outliers')
plt.show()

Producción:

print(mean) # mean of the numeric array with outliers

Producción:

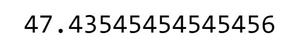
Ahora, winsorizamos la array en un 10%, es decir, winsorizamos el 5% de los valores más altos y el 5% del valor más bajo de la array:

WinsorizedArray = winsorize(array,(0.05,0.05))
  
plt.boxplot(WinsorizedArray)
plt.title('Winsorized array')
plt.show()

Producción:

WinsorizedMean = np.mean(WinsorizedArray)
print(WinsorizedMean)

Producción:

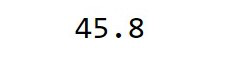
En este caso, solo hay un ligero cambio en el valor medio de los datos.

Ahora, veamos un ejemplo donde los valores atípicos están presentes solo en un extremo de los datos.

# Creating another array with 100 random values
array2 = [np.random.randint(100) for i in range(100)] 
std = np.std(array2)
mean = np.mean(array2)
AlreadySelected = []
# Creating outliers on the upper end
i = 0 
while (i<5):
    x = np.random.choice(array2) # Randomly selecting a value from the array
    y = x + mean*4
    array2 = np.append(array2,y)
    if (x not in AlreadySelected):
        AlreadySelected.append(y)
  
        i+=1
          
    else:
        continue
          
plt.boxplot(array2)
plt.title('Array with outliers')
plt.show()

Producción:

OutlierArray2Mean = np.mean(array2)
print(OutlierArray2Mean)

Producción:

WinsorizedArray2 = winsorize(array2,(0.1,0.1))
# In this case, the lower 10% values of 
# the data will have their values set equal to the value of the data point at 
#the 10th percentile.
  
plt.boxplot(WinsorizedArray2)
plt.show()
  
WinsorizedArray2Mean = np.mean(WinsorizedArray2)

Producción:

WinsorizedArray2Mean = np.mean(WinsorizedArray2)
print(WinsorizedArray2Mean)

Producción:

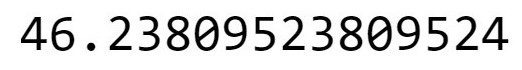
En este caso, hay una diferencia significativa en el valor medio.