XGBoost

XgBoost significa Extreme Gradient Boosting, que fue propuesto por los investigadores de la Universidad de Washington. Es una biblioteca escrita en C++ que optimiza el entrenamiento para Gradient Boosting.

Antes de comprender el XGBoost, primero debemos comprender los árboles, especialmente el árbol de decisión :

Árbol de decisión:

Un árbol de decisión es una estructura de árbol similar a un diagrama de flujo, donde cada Node interno denota una prueba en un atributo, cada rama representa un resultado de la prueba y cada Node de hoja (Node terminal) contiene una etiqueta de clase.

Un árbol se puede «aprender» dividiendo el conjunto fuente en subconjuntos en función de una prueba de valor de atributo. Este proceso se repite en cada subconjunto derivado de una manera recursiva llamada partición recursiva. La recursividad se completa cuando el subconjunto en un Node tiene el mismo valor de la variable de destino, o cuando la división ya no agrega valor a las predicciones.

Embolsado :

Un clasificador de embolsado es un metaestimador de conjunto que ajusta los clasificadores base cada uno en subconjuntos aleatorios del conjunto de datos original y luego agrega sus predicciones individuales (ya sea por votación o por promedio) para formar una predicción final. Un metaestimador de este tipo se puede utilizar normalmente como una forma de reducir la varianza de un estimador de caja negra (por ejemplo, un árbol de decisión), introduciendo la aleatorización en su procedimiento de construcción y luego convirtiéndolo en un conjunto.
Cada clasificador base se entrena en paralelo con un conjunto de entrenamiento que se genera extrayendo aleatoriamente, con reemplazo, N ejemplos (o datos) del conjunto de datos de entrenamiento original, donde N es el tamaño del conjunto de entrenamiento original. El conjunto de entrenamiento para cada uno de los clasificadores base es independiente entre sí. Muchos de los datos originales pueden repetirse en el conjunto de entrenamiento resultante, mientras que otros pueden omitirse.

El embolsado reduce el sobreajuste (varianza) al promediar o votar, sin embargo, esto conduce a un aumento en el sesgo, que se compensa con la reducción de la varianza.

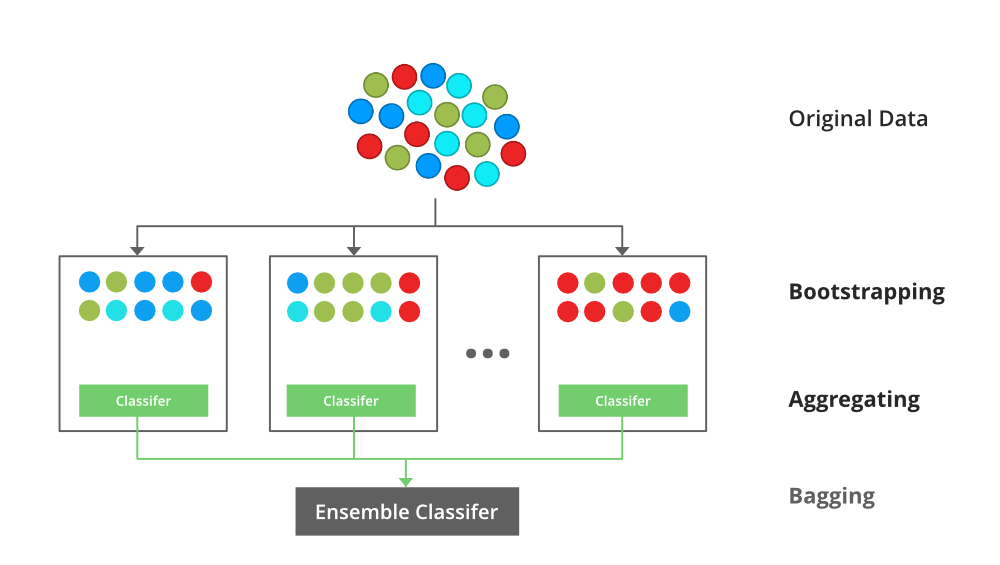
Clasificador de embolsado

Bosque aleatorio :

Cada árbol de decisión tiene una varianza alta, pero cuando los combinamos todos juntos en paralelo, la varianza resultante es baja ya que cada árbol de decisión se entrena perfectamente en esos datos de muestra en particular y, por lo tanto, la salida no depende de un árbol de decisión sino de múltiples decisiones. árboles. En el caso de un problema de clasificación, la salida final se obtiene utilizando el clasificador de votación por mayoría. En el caso de un problema de regresión, la salida final es la media de todas las salidas. Esta parte es Agregación.

La idea básica detrás de esto es combinar múltiples árboles de decisión para determinar el resultado final en lugar de depender de árboles de decisión individuales.
Random Forest tiene múltiples árboles de decisión como modelos básicos de aprendizaje. Realizamos aleatoriamente muestreo de filas y muestreo de características del conjunto de datos formando conjuntos de datos de muestra para cada modelo. Esta parte se llama Bootstrap.

Impulso :

Boosting es una técnica de modelado de conjuntos que intenta construir un clasificador fuerte a partir del número de clasificadores débiles. Se realiza construyendo un modelo utilizando modelos débiles en serie. En primer lugar, se construye un modelo a partir de los datos de entrenamiento. Luego se construye el segundo modelo que trata de corregir los errores presentes en el primer modelo. Este procedimiento continúa y se agregan modelos hasta que se pronostica correctamente el conjunto completo de datos de entrenamiento o se agrega el número máximo de modelos.

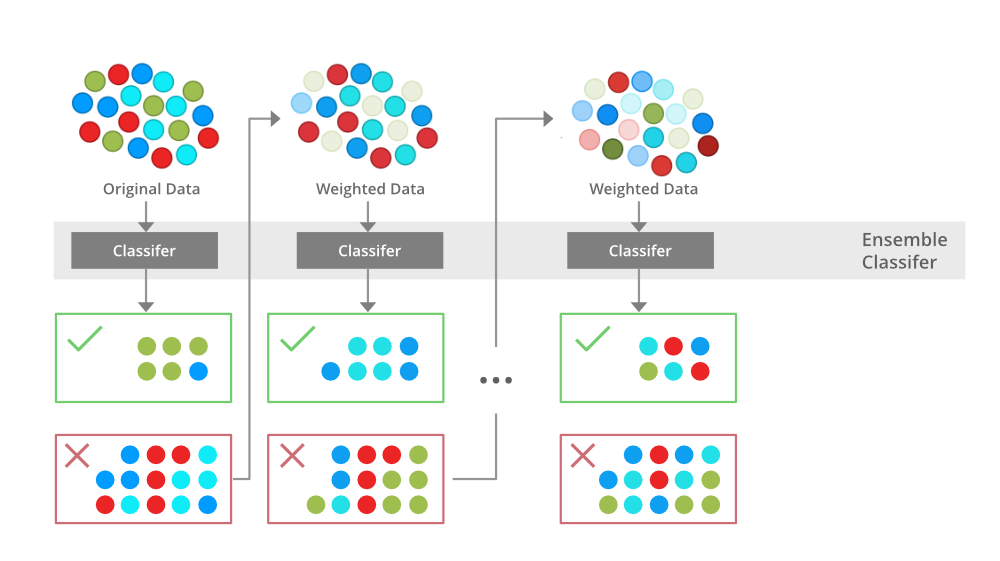
impulsar

Aumento de gradiente

Gradient Boosting es un algoritmo de impulso popular. En el aumento de gradiente, cada predictor corrige el error de su predecesor. A diferencia de Adaboost, los pesos de las instancias de entrenamiento no se modifican, sino que cada predictor se entrena utilizando los errores residuales del predecesor como etiquetas.

Existe una técnica llamada Gradient Boosted Trees cuyo alumno base es CART (Classification and Regression Trees).

XGBoost es una implementación de árboles de decisión Gradient Boost. Los modelos XGBoost dominan en gran medida en muchas competiciones de Kaggle.

En este algoritmo, los árboles de decisión se crean en forma secuencial. Los pesos juegan un papel importante en XGBoost. Se asignan pesos a todas las variables independientes que luego se introducen en el árbol de decisión que predice los resultados. El peso de las variables predichas incorrectamente por el árbol aumenta y estas variables luego se alimentan al segundo árbol de decisión. Estos clasificadores/predictores individuales luego se agrupan para dar un modelo fuerte y más preciso. Puede funcionar en problemas de regresión, clasificación, clasificación y predicción definida por el usuario.

Matemáticas detrás de XgBoost

Antes de comenzar con las matemáticas sobre Gradient Boosting, aquí hay un ejemplo simple de un CART que clasifica si a alguien le gustará un hipotético juego de computadora X. El ejemplo de árbol está a continuación:

Los puntajes de predicción de cada árbol de decisión individual luego se suman para obtener Si observa el ejemplo, un hecho importante es que los dos árboles intentan complementarse entre sí. Matemáticamente, podemos escribir nuestro modelo en la forma

$\hat{y}_{i} = \sum_{k=1}^{K} f_k(x_i), f_k \epsilon \mathcal{F} \\$

donde, K es el número de árboles, f es el espacio funcional de F, F es el conjunto de CART posibles. La función objetivo para el modelo anterior viene dada por:

$obj(\theta) = \sum_{i}^{n} l(y_{i}, \hat{y}_{i}) + \sum_{k=1}^K \Omega(f_{k}) \\$

donde, el primer término es la función de pérdida y el segundo es el parámetro de regularización. Ahora, en lugar de aprender todo el árbol a la vez, lo que dificulta la optimización, aplicamos la estrategia aditiva, minimizamos la pérdida de lo que hemos aprendido y agregamos un nuevo árbol que se puede resumir a continuación:

$\hat{y}_i^{(0)} =0\\ \hat{y}_i^{(1)} = f_1(x_i) = \hat{y}_i^{(0)} + f_1(x_i)\\ \hat{y}_i^{(2)} = f_1(x_i) + f_2(x_i)= \hat{y}_i^{(1)} + f_2(x_i)\\ ....\\ \hat{y}_i^{(t)} = \sum_{k=1}^t f_k(x_i)= \hat{y}_i^{(t-1)} + f_t(x_i)$

La función objetivo del modelo anterior se puede definir como:

$obj^{(t)} = \sum_{i=1}^{n} l(y_i, \hat{y}_{i}^{(t)}) + \sum_{i=1}^t\Omega(f_i) \\ = \sum_{i=1}^{n} l(y_i, \hat{y}_{i}^{(t-1)} + f_{t}(x_i)) + \Omega(f_t) + constant$

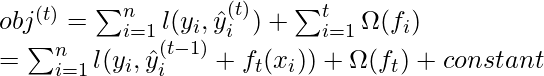
$obj^{(t)} = \sum_{i=1}^n (y_{i} - (\hat{y}_{i}^{(t-1)} + f_t(x_i)))^2 + \sum_{i=1}^t\Omega(f_i) \\ = \sum_{i=1}^n [2(\hat{y}_i^{(t-1)} - y_i)f_t(x_i) + f_t(x_i)^2] + \Omega(f_t) + constant$

Ahora, apliquemos la expansión de la serie de Taylor hasta el segundo orden:

$obj^{(t)} = \sum_{i=1}^{n} [l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_{i} f_{t}^2(x_i)] + \Omega(f_t) + constant$

donde g_i y h_i se pueden definir como:

$g_i = \partial_{\hat{y}_i^{(t-1)}} l(y_i, \hat{y}_i^{(t-1)})\\ h_i = \partial_{\hat{y}_i^{(t-1)}}^2 l(y_i, \hat{y}_i^{(t-1)})$

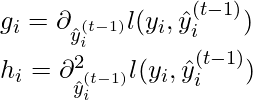
Simplificando y eliminando la constante:

$\sum_{i=1}^n [g_{i} f_{t}(x_i) + \frac{1}{2} h_{i} f_{t}^2(x_i)] + \Omega(f_t)$

Ahora, definimos el término de regularización, pero primero necesitamos definir el modelo:

$f_t(x) = w_{q(x)}, w \in R^{T}, q:R^d\rightarrow \{1,2,...,T\}$

Aquí, w es el vector de puntajes en las hojas del árbol, q es la función que asigna cada punto de datos a la hoja correspondiente y T es el número de hojas. El término de regularización se define entonces por:

$\Omega(f) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2$

Ahora, nuestra función objetivo se convierte en:

$obj^{(t)} \approx \sum_{i=1}^n [g_i w_{q(x_i)} + \frac{1}{2} h_i w_{q(x_i)}^2] + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2\\ = \sum^T_{j=1} [(\sum_{i\in I_j} g_i) w_j + \frac{1}{2} (\sum_{i\in I_j} h_i + \lambda) w_j^2 ] + \gamma T$

Ahora, simplificamos la expresión anterior:

$obj^{(t)} = \sum^T_{j=1} [G_jw_j + \frac{1}{2} (H_j+\lambda) w_j^2] +\gamma T$

dónde,

$G_j = \sum_{i\in I_j} g_i\\ H_j = \sum_{i\in I_j} h_i$

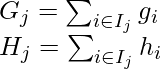
En esta ecuación, w_j son independientes entre sí, lo mejor $w_j$ para una estructura dada q(x) y la mejor reducción objetiva que podemos obtener es:

$w_j^{\ast} = -\frac{G_j}{H_j+\lambda}\\ \text{obj}^{\ast} = -\frac{1}{2} \sum_{j=1}^T \frac{G_j^2}{H_j+\lambda} + \gamma T$

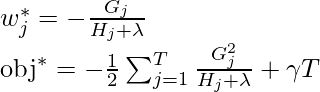
donde, \gamma es el parámetro de poda, es decir, la ganancia de información mínima para realizar la división.

Ahora, tratamos de medir qué tan bueno es el árbol, no podemos optimizar el árbol directamente, trataremos de optimizar un nivel del árbol a la vez. Específicamente, tratamos de dividir una hoja en dos hojas, y la puntuación que obtiene es

$Gain = \frac{1}{2} \left[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}\right] - \gamma$

Cálculo de la Ganancia de Información

Ejemplos

Consideremos un conjunto de datos de ejemplo:

años de experiencia	Brecha	Salario anual (en 100k)
1	norte	4
1.5	Y	4
2.5	Y	5.5
3	norte	7
5	norte	7.5
6	norte	8

Primero tomamos el alumno base, por defecto el modelo base siempre toma el salario promedio, es decir $F_0 =6$ (100k). Ahora, calculamos los valores residuales:

años de experiencia	Brecha	Salario anual (en 100k)	Derechos residuales de autor
1	norte	4	-2
1.5	Y	4	-2
2.5	Y	5.5	-0.5
3	norte	7	1
5	norte	7.5	1.5
6	norte	8	2

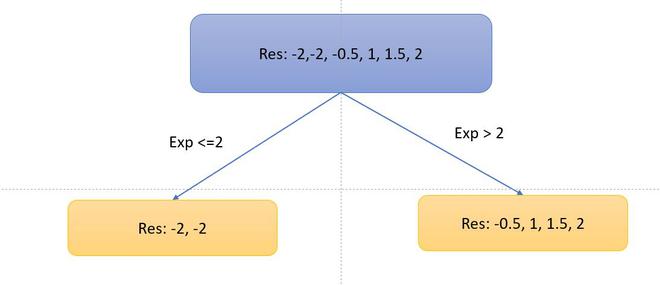
Ahora, consideremos el árbol de decisiones, dividiremos los datos según la experiencia <=2 o de otra manera.

Ahora, calculemos las métricas de similitud del lado izquierdo y derecho. Dado que es el problema de regresión, la métrica de similitud será:

$S_m = \frac{\sum (res)^{2}}{n_{res} + \lambda}$

donde, \lambda = hiperparámetro

y para el problema de clasificación:

$S = \frac{\sum (res)^{2}}{P_{r} + (1-P_{r})}$

donde, P_r = probabilidad de cualquier lado izquierdo del lado derecho. Tomemos las $\lambda = 1$ métricas de similitud del lado izquierdo:

$S_{L} = \frac{(-4)^2}{2+1} = \frac{16}{3} =5.33$ and for the right side.

$S_{R} = \frac{(4)^2}{4+1} = \frac{16}{5} =3.2$ and for the top branch:

$S_{T} = \frac{1}{7} =0.143$ .

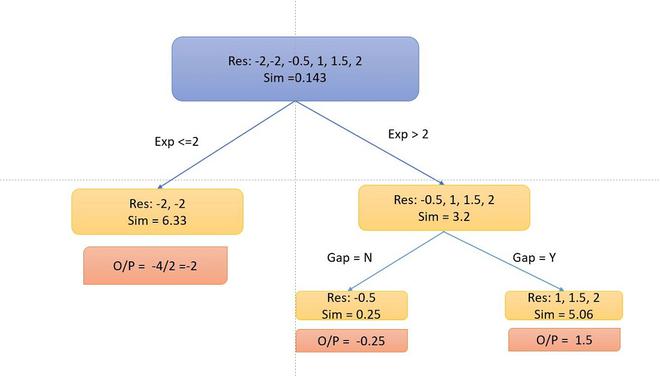
Ahora, la ganancia de información de esta división es:

$GAIN = S_{L} + S_{R}- S_{T} = 6.33 +3.2 -0.143 = 9.328$

De manera similar, podemos probar múltiples divisiones y calcular la ganancia de información. Tomaremos la división con la mayor ganancia de información. Tomemos por ahora esta ganancia de información. Además, dividiremos el árbol de decisión si hay una brecha o no.

Ahora, como puede notar, no me dividí en el lado izquierdo porque la ganancia de información se vuelve negativa. Entonces, solo realizamos split en el lado derecho.
Para calcular el resultado particular, seguimos el árbol de decisión multiplicado por una tasa de aprendizaje \alpha (tomemos 0,5) y lo sumamos con el alumno anterior (alumno base para el primer árbol), es decir, para el punto de datos 1: o/p = 6 + 0,5 *-2 =5. Así se convierte nuestra mesa.
Del mismo modo, el algoritmo produce más de un árbol de decisión y los combina de forma aditiva para generar mejores estimaciones.

Optimización y Mejora

Optimización del sistema:

Regularización : Dado que el conjunto de decisiones, los árboles a veces pueden dar lugar a muy complejas. XGBoost usa la regularización de Lasso y Ridge Regression para penalizar el modelo altamente complejo.
Paralelización y bloque de caché : en XGboost, no podemos entrenar múltiples árboles en paralelo, pero puede generar los diferentes Nodes del árbol en paralelo. Para eso, los datos deben ordenarse en orden. Para reducir el costo de clasificación, almacena los datos en bloques. Almacenó los datos en el formato de columna comprimida, con cada columna ordenada por el valor de característica correspondiente. Este conmutador mejora el rendimiento algorítmico al compensar cualquier sobrecarga de paralelización en el cálculo.
Poda de árboles: XGBoost usa el parámetro max_ depth como se especifica en los criterios de detención para la división de la rama y comienza a podar los árboles hacia atrás. Este enfoque de profundidad primero mejora significativamente el rendimiento computacional.
Cache-Awareness y cálculo fuera de puntuación : este algoritmo ha sido diseñado para hacer un uso eficiente de los recursos de hardware. Esto se logra mediante el conocimiento de la memoria caché mediante la asignación de búferes internos en cada subproceso para almacenar estadísticas de gradiente. Otras mejoras, como la «computación fuera del núcleo», optimizan el espacio disponible en el disco mientras manejan grandes marcos de datos que no caben en la memoria. En el cálculo fuera del núcleo, Xgboost intenta minimizar el conjunto de datos comprimiéndolo.
Conciencia de escasez: XGBoost puede manejar datos escasos que pueden generarse a partir de pasos de preprocesamiento o valores faltantes. Utiliza un algoritmo especial de búsqueda de división incorporado que puede manejar diferentes tipos de patrones de dispersión.
Esbozo de cuantil ponderado: XGBoost tiene incorporado el algoritmo de esbozo de cuantil ponderado distribuido que facilita la búsqueda efectiva de los puntos de división óptimos entre conjuntos de datos ponderados.
Validación cruzada : la implementación de XGboost viene con un método de validación cruzada integrado. Esto ayuda al algoritmo a evitar el sobreajuste cuando el conjunto de datos no es tan grande.

Referencias:

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA