En este artículo, aprendamos sobre la regresión lineal múltiple usando scikit-learn en el lenguaje de programación Python.
La regresión es un método estadístico para determinar la relación entre las características y una variable de resultado o resultado. El aprendizaje automático se utiliza como un método para el modelado predictivo, en el que se emplea un algoritmo para pronosticar resultados continuos. La regresión lineal múltiple, a menudo conocida como regresión múltiple, es un método estadístico que predice el resultado de una variable de respuesta mediante la combinación de numerosas variables explicativas. La regresión múltiple es una variante de la regresión lineal (mínimos cuadrados ordinarios) en la que solo se utiliza una variable explicativa.
Imputación Matemática:
Para mejorar la predicción, se combinan más factores independientes. La siguiente es la relación lineal entre las variables dependientes e independientes:
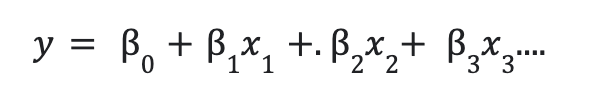
aquí, y es la variable dependiente.
- x1, x2,x3,… son variables independientes.
- b0 = intersección de la línea.
- b1, b2,… son coeficientes.
para una línea de regresión lineal simple es de la forma:
y = mx+c
por ejemplo, si tomamos un ejemplo simple,:
característica 1: televisión
característica 2: radio
característica 3: Periódico
variable de salida: ventas
Las variables independientes son las funciones función 1, función 2 y función 3. La variable dependiente son las ventas. La ecuación para este problema será:
y = b0+b1x1+b2x2+b3x3
x1, x2 y x3 son las variables características.
En este ejemplo, usamos scikit-learn para realizar una regresión lineal. Como tenemos múltiples variables de características y una sola variable de resultado, es una regresión lineal múltiple. Veamos cómo hacer esto paso a paso.
Implementación paso a paso
Paso 1: Importa los paquetes necesarios
Se importan los paquetes necesarios como pandas, NumPy, sklearn, etc….
Python3
# importing modules and packages import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error, mean_absolute_error from sklearn import preprocessing
Paso 2: importa el archivo CSV:
El archivo CSV se importa mediante el método pd.read_csv() . Para acceder al archivo CSV haga clic aquí. La columna ‘No’ se elimina porque ya hay un índice presente. El método df.head() se usa para recuperar las primeras cinco filas del marco de datos. El atributo df.columns devuelve el nombre de las columnas. Los nombres de columna que comienzan con ‘X’ son las características independientes en nuestro conjunto de datos. La columna ‘Y precio de la vivienda de la unidad de área’ es la columna de la variable dependiente. Como el número de variables independientes o exploratorias es más de uno, se trata de una regresión multilineal.
Para ver y descargar el archivo CSV, haga clic aquí .
Python3
# importing data
df = pd.read_csv('Real estate.csv')
df.drop('No', inplace = True,axis=1)
print(df.head())
print(df.columns)
Producción:
X1 fecha de transacción X2 edad de la casa … X6 longitud Y precio de la casa de la unidad de área
0 2012.917 32.0 … 121.54024 37.9
1 2012.917 19,5 … 121,53951 42,2
2 2013.583 13,3 … 121,54391 47,3
3 2013.500 13,3 … 121,54391 54,8
4 2012.833 5.0 … 121.54245 43.1
[5 filas x 7 columnas]
Índice ([‘X1 fecha de transacción’, ‘X2 edad de la casa’,
‘Distancia X3 a la estación MRT más cercana’,
‘X4 número de tiendas de conveniencia’, ‘X5 latitud’, ‘X6 longitud’,
‘Y precio de la vivienda por unidad de superficie’],
dtype=’objeto’)
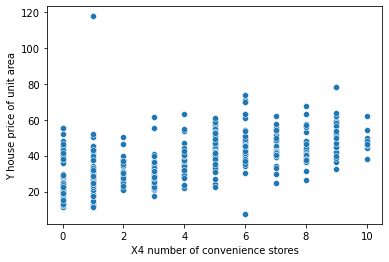
Paso 3: Cree un diagrama de dispersión para visualizar los datos:
Se crea un diagrama de dispersión para visualizar la relación entre la variable independiente ‘X4 número de tiendas de conveniencia’ y la función dependiente ‘Y precio de la vivienda por unidad de área’.
Python3
# plotting a scatterplot sns.scatterplot(x='X4 number of convenience stores', y='Y house price of unit area', data=df)
Producción:
Paso 4: Crear variables de características:
Para modelar los datos, necesitamos crear variables de características, la variable X contiene variables independientes y la variable y contiene una variable dependiente. Las variables de característica X e Y se imprimen para ver los datos.
Python3
# creating feature variables
X = df.drop('Y house price of unit area',axis= 1)
y = df['Y house price of unit area']
print(X)
print(y)
Producción:
X1 Fecha de transacción X2 Edad de la casa … X5 Latitud X6 Longitud
0 2012.917 32.0 … 24.98298 121.54024
1 2012.917 19.5 … 24.98034 121.53951
2 2013.583 13.3 … 24.98746 121.54391
3 2013.500 13.3 … 24.98746 121.54391
4 2012.833 5.0 … 24.97937 121.54245
.. … … … … …
409 2013.000 13.7 … 24.94155 121.50381
410 2012.667 5.6 … 24.97433 121.54310
411 2013.250 18.8 … 24.97923 121.53986
412 2013.000 8.1 … 24.96674 121.54067
413 2013.500 6.5 … 24.97433 121.54310
[414 filas x 6 columnas]
0 37,9
1 42,2
2 47,3
3 54,8
4 43,1
…
409 15.4
410 50,0
411 40.6
412 52.5
413 63,9
Nombre: Y precio de la vivienda de la unidad de área, Longitud: 414, dtype: float64
Paso 5: dividir los datos en conjuntos de entrenamiento y prueba:
Aquí, el método train_test_split() se usa para crear conjuntos de entrenamiento y prueba, las variables de característica se pasan en el método. el tamaño de la prueba se da como 0.3, lo que significa que el 30 % de los datos van a los conjuntos de prueba, y los datos del conjunto del tren contienen el 70 % de los datos. el estado aleatorio se da para la reproducibilidad de los datos.
Python3
# creating train and test sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.3, random_state=101)
Paso 6: Cree un modelo de regresión lineal
Se crea un modelo de regresión lineal simple. La clase LinearRegression() se usa para crear un modelo de regresión simple, la clase se importa del paquete sklearn.linear_model.
Python3
# creating a regression model model = LinearRegression()
Paso 7: ajuste el modelo con datos de entrenamiento.
Después de crear el modelo, se ajusta a los datos de entrenamiento. El modelo adquiere conocimiento sobre las estadísticas del modelo de entrenamiento. El método fit() se utiliza para ajustar los datos.
Python3
# fitting the model model.fit(X_train,y_train)
Paso 8: Hacer predicciones sobre el conjunto de datos de prueba.
En este método model.predict() se usa para hacer predicciones sobre los datos X_test, ya que los datos de prueba son datos invisibles y el modelo no tiene conocimiento sobre las estadísticas del conjunto de prueba.
Python3
# making predictions predictions = model.predict(X_test)
Paso 9: Evaluar el modelo con métricas.
El modelo de regresión multilineal se evalúa con las métricas mean_squared_error y mean_absolute_error. cuando se compara con la media de la variable objetivo, comprenderemos qué tan bien predice nuestro modelo. mean_squared_error es la media de la suma de los residuos. mean_absolute_error es la media de los errores absolutos del modelo. Cuanto menor sea el error, mejor será el rendimiento del modelo.
error absoluto medio = es la media de la suma de los valores absolutos de los residuos.
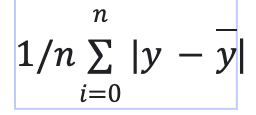
error cuadrático medio = es la media de la suma de los cuadrados de los residuos.
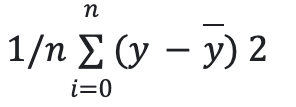
- y = valor real
- y sombrero = predicciones
Python3
# model evaluation print( 'mean_squared_error : ', mean_squared_error(y_test, predictions)) print( 'mean_absolute_error : ', mean_absolute_error(y_test, predictions))
Producción:
mean_squared_error : 46.21179783493418 mean_absolute_error : 5.392293684756571
Para la recopilación de datos, debe haber una discrepancia significativa entre los números. Si desea ignorar los valores atípicos en sus datos, MAE es una alternativa preferible, pero si desea tenerlos en cuenta en su función de pérdida, MSE/RMSE es el camino a seguir. MSE siempre es mayor que MAE en la mayoría de los casos, MSE es igual a MAE solo cuando las magnitudes de los errores son las mismas.
Código:
Aquí está el código completo junto, combinando los pasos anteriores.
Python3
# importing modules and packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn import preprocessing
# importing data
df = pd.read_csv('Real estate.csv')
df.drop('No', inplace=True, axis=1)
print(df.head())
print(df.columns)
# plotting a scatterplot
sns.scatterplot(x='X4 number of convenience stores',
y='Y house price of unit area', data=df)
# creating feature variables
X = df.drop('Y house price of unit area', axis=1)
y = df['Y house price of unit area']
print(X)
print(y)
# creating train and test sets
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=101)
# creating a regression model
model = LinearRegression()
# fitting the model
model.fit(X_train, y_train)
# making predictions
predictions = model.predict(X_test)
# model evaluation
print('mean_squared_error : ', mean_squared_error(y_test, predictions))
print('mean_absolute_error : ', mean_absolute_error(y_test, predictions))
Producción:
X1 fecha de transacción X2 edad de la casa … X6 longitud Y precio de la casa de la unidad de área
0 2012.917 32.0 … 121.54024 37.9
1 2012.917 19,5 … 121,53951 42,2
2 2013.583 13,3 … 121,54391 47,3
3 2013.500 13,3 … 121,54391 54,8
4 2012.833 5.0 … 121.54245 43.1
[5 filas x 7 columnas]
Índice ([‘X1 fecha de transacción’, ‘X2 edad de la casa’,
‘Distancia X3 a la estación MRT más cercana’,
‘X4 número de tiendas de conveniencia’, ‘X5 latitud’, ‘X6 longitud’,
‘Y precio de la vivienda por unidad de superficie’],
dtype=’objeto’)
X1 Fecha de transacción X2 Edad de la casa … X5 Latitud X6 Longitud
0 2012.917 32.0 … 24.98298 121.54024
1 2012.917 19.5 … 24.98034 121.53951
2 2013.583 13.3 … 24.98746 121.54391
3 2013.500 13.3 … 24.98746 121.54391
4 2012.833 5.0 … 24.97937 121.54245
.. … … … … …
409 2013.000 13.7 … 24.94155 121.50381
410 2012.667 5.6 … 24.97433 121.54310
411 2013.250 18.8 … 24.97923 121.53986
412 2013.000 8.1 … 24.96674 121.54067
413 2013.500 6.5 … 24.97433 121.54310
[414 filas x 6 columnas]
0 37,9
1 42,2
2 47,3
3 54,8
4 43,1
…
409 15.4
410 50,0
411 40.6
412 52.5
413 63,9
Nombre: Y precio de la vivienda de la unidad de área, Longitud: 414, dtype: float64
error_cuadrado_medio: 46.21179783493418
error_absoluto_medio: 5.392293684756571
Publicación traducida automáticamente
Artículo escrito por isitapol2002 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA