Este artículo tiene como objetivo implementar la clasificación de documentos usando Naïve Bayes usando python.
Implementación paso a paso:
Paso 1:
- Ingrese el número total de documentos del usuario.
- Ingrese el texto y la clase de cada documento y divídalo en una lista.
- Cree una array 2D y agregue cada lista de documentos a una array.
- Usando una estructura de datos Set, almacene todas las palabras clave en una lista.
- Introduzca el texto a clasificar por el usuario.
Python3
print('\n *-----* Classification using Naïve bayes *-----* \n')
total_documents = int(input("Enter the Total Number of documents: "))
doc_class = []
i = 0
keywords = []
while not i == total_documents:
doc_class.append([])
text = input(f"\nEnter the text of Doc-{i+1} : ").lower()
clas = input(f"Enter the class of Doc-{i+1} : ")
doc_class[i].append(text.split())
doc_class[i].append(clas)
keywords.extend(text.split())
i = i+1
keywords = set(keywords)
keywords = list(keywords)
keywords.sort()
to_find = input("\nEnter the Text to classify using Naive Bayes: ").lower().split()
Paso 2:
- Cree una lista vacía llamada «probability_table».
- Cuente todas las apariciones de todas las palabras clave en cada documento y guárdelas en la lista «probability_table».
Python3
probability_table = []
for i in range(total_documents):
probability_table.append([])
for j in keywords:
probability_table[i].append(0)
doc_id = 1
for i in range(total_documents):
for k in range(len(keywords)):
if keywords[k] in doc_class[i][0]:
probability_table[i][k] += doc_class[i][0].count(keywords[k])
print('\n')
Paso 3:
- Importe una tabla bonita para mostrar la lista «probability_table» en un formato tabular ordenado.
- Dar el título de la Tabla como ‘Probabilidad de Documentos’
- Imprime la tabla.
Python3
import prettytable
keywords.insert(0, 'Document ID')
keywords.append("Class")
Prob_Table = prettytable.PrettyTable()
Prob_Table.field_names = keywords
Prob_Table.title = 'Probability of Documents'
x=0
for i in probability_table:
i.insert(0,x+1)
i.append(doc_class[x][1])
Prob_Table.add_row(i)
x=x+1
print(Prob_Table)
print('\n')
for i in probability_table:
i.pop(0)
Paso 4:
- Cuente el número de palabras totales que pertenecen a la clase ‘+’.
- Cuente el número de palabras totales que pertenecen a la clase ‘-‘.
- Cuente el número de documentos totales que pertenecen a la clase ‘+’.
- Cuente el número de documentos totales que pertenecen a la clase ‘-‘.
Python3
totalpluswords=0 totalnegwords=0 totalplus=0 totalneg=0 vocabulary=len(keywords)-2 for i in probability_table: if i[len(i)-1]=="+": totalplus+=1 totalpluswords+=sum(i[0:len(i)-1]) else: totalneg+=1 totalnegwords+=sum(i[0:len(i)-1]) keywords.pop(0) keywords.pop(len(keywords)-1)
Paso-5:
- Para superar el problema de frecuencia cero, utilice la siguiente fórmula para encontrar la probabilidad final de clasificar cada palabra presente en el texto.
P(Palabra/Clase) = (Núm. de ocurrencias de palabra en clase+1) / (Número total de palabras presentes en clase + Total de palabras clave)
- Formatee la probabilidad de cada palabra con una precisión de 4 dígitos.
Python3
#For positive class
temp=[]
for i in to_find:
count=0
x=keywords.index(i)
for j in probability_table:
if j[len(j)-1]=="+":
count=count+j[x]
temp.append(count)
count=0
for i in range(len(temp)):
temp[i]=format((temp[i]+1)/(vocabulary+totalpluswords),".4f")
print()
temp=[float(f) for f in temp]
print("Probabilities of Each word to be in '+' class are: ")
h=0
for i in to_find:
print(f"P({i}/+) = {temp[h]}")
h=h+1
print()
Paso-6:
- Encuentre la probabilidad final de Cada clase usando la fórmula de Naïve Bayes.
- Formatee el resultado final con una precisión de 8 dígitos.
Python3
pplus=float(format((totalplus)/(totalplus+totalneg),".8f"))
for i in temp:
pplus=pplus*i
pplus=format(pplus,".8f")
print("probability of Given text to be in '+' class is :",pplus)
print()
Paso-7:
- Realice también los pasos 5 y 6 para las clases negativas.
Python3
#For Negative class
temp=[]
for i in to_find:
count=0
x=keywords.index(i)
for j in probability_table:
if j[len(j)-1]=="-":
count=count+j[x]
temp.append(count)
count=0
for i in range(len(temp)):
temp[i]=format((temp[i]+1)/(vocabulary+totalnegwords),".4f")
print()
temp=[float(f) for f in temp]
print("Probabilities of Each word to be in '-' class are: ")
h=0
for i in to_find:
print(f"P({i}/-) = {temp[h]}")
h=h+1
print()
pneg=float(format((totalneg)/(totalplus+totalneg),".8f"))
for i in temp:
pneg=pneg*i
pneg=format(pneg,".8f")
print("probability of Given text to be in '-' class is :",pneg)
print('\n')
Paso-8:
- Compara las probabilidades finales de ambas clases.
- Imprime el resultado final.
Python3
if pplus>pneg:
print(f"Using Naive Bayes Classification, We can clearly say that the given text belongs to '+' class with probability {pplus}")
else:
print(f"Using Naive Bayes Classification, We can clearly say that the given text belongs to '-' class with probability {pneg}")
print('\n')
A continuación se muestra la implementación completa:
Python3
print('\n *-----* Classification using Naïve bayes *-----* \n')
total_documents = int(input("Enter the Total Number of documents: "))
doc_class = []
i = 0
keywords = []
while not i == total_documents:
doc_class.append([])
text = input(f"\nEnter the text of Doc-{i+1} : ").lower()
clas = input(f"Enter the class of Doc-{i+1} : ")
doc_class[i].append(text.split())
doc_class[i].append(clas)
keywords.extend(text.split())
i = i+1
keywords = set(keywords)
keywords = list(keywords)
keywords.sort()
to_find = input("\nEnter the Text to classify using Naive Bayes: ").lower().split()
probability_table = []
for i in range(total_documents):
probability_table.append([])
for j in keywords:
probability_table[i].append(0)
doc_id = 1
for i in range(total_documents):
for k in range(len(keywords)):
if keywords[k] in doc_class[i][0]:
probability_table[i][k] += doc_class[i][0].count(keywords[k])
print('\n')
import prettytable
keywords.insert(0, 'Document ID')
keywords.append("Class")
Prob_Table = prettytable.PrettyTable()
Prob_Table.field_names = keywords
Prob_Table.title = 'Probability of Documents'
x=0
for i in probability_table:
i.insert(0,x+1)
i.append(doc_class[x][1])
Prob_Table.add_row(i)
x=x+1
print(Prob_Table)
print('\n')
for i in probability_table:
i.pop(0)
totalpluswords=0
totalnegwords=0
totalplus=0
totalneg=0
vocabulary=len(keywords)-2
for i in probability_table:
if i[len(i)-1]=="+":
totalplus+=1
totalpluswords+=sum(i[0:len(i)-1])
else:
totalneg+=1
totalnegwords+=sum(i[0:len(i)-1])
keywords.pop(0)
keywords.pop(len(keywords)-1)
#For positive class
temp=[]
for i in to_find:
count=0
x=keywords.index(i)
for j in probability_table:
if j[len(j)-1]=="+":
count=count+j[x]
temp.append(count)
count=0
for i in range(len(temp)):
temp[i]=format((temp[i]+1)/(vocabulary+totalpluswords),".4f")
print()
temp=[float(f) for f in temp]
print("Probabilities of Each word to be in '+' class are: ")
h=0
for i in to_find:
print(f"P({i}/+) = {temp[h]}")
h=h+1
print()
pplus=float(format((totalplus)/(totalplus+totalneg),".8f"))
for i in temp:
pplus=pplus*i
pplus=format(pplus,".8f")
print("probability of Given text to be in '+' class is :",pplus)
print()
#For Negative class
temp=[]
for i in to_find:
count=0
x=keywords.index(i)
for j in probability_table:
if j[len(j)-1]=="-":
count=count+j[x]
temp.append(count)
count=0
for i in range(len(temp)):
temp[i]=format((temp[i]+1)/(vocabulary+totalnegwords),".4f")
print()
temp=[float(f) for f in temp]
print("Probabilities of Each word to be in '-' class are: ")
h=0
for i in to_find:
print(f"P({i}/-) = {temp[h]}")
h=h+1
print()
pneg=float(format((totalneg)/(totalplus+totalneg),".8f"))
for i in temp:
pneg=pneg*i
pneg=format(pneg,".8f")
print("probability of Given text to be in '-' class is :",pneg)
print('\n')
if pplus>pneg:
print(f"Using Naive Bayes Classification, We can clearly say that the given text belongs to '+' class with probability {pplus}")
else:
print(f"Using Naive Bayes Classification, We can clearly say that the given text belongs to '-' class with probability {pneg}")
print('\n')
Captura de pantalla de salida:

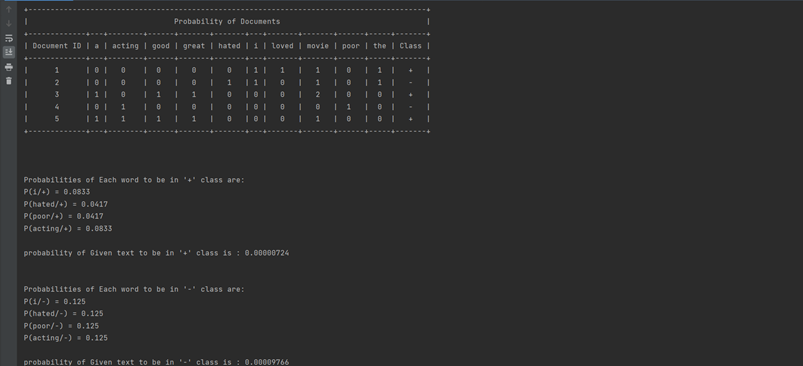

Publicación traducida automáticamente
Artículo escrito por kothavvsaakash y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA