En este artículo, aprenderemos ‘Qué son el sesgo y la varianza para un modelo de aprendizaje automático y cuál debería ser su estado óptimo.
Hay varias formas de evaluar un modelo de aprendizaje automático. Podemos usar MSE (Mean Squared Error) para la regresión; Precisión, Recall y ROC (Receiver of Characteristics) para un Problema de Clasificación junto con Error Absoluto. De manera similar, el sesgo y la varianza nos ayudan a ajustar los parámetros y decidir los modelos que mejor se ajustan entre varios construidos.
El sesgo es un tipo de error que ocurre debido a suposiciones incorrectas sobre los datos, como suponer que los datos son lineales cuando en realidad siguen una función compleja. Por otro lado, la varianza se introduce con una alta sensibilidad a las variaciones en los datos de entrenamiento. Este también es un tipo de error, ya que queremos que nuestro modelo sea resistente al ruido.
Antes de llegar a las definiciones matemáticas, necesitamos saber acerca de las variables y funciones aleatorias. Digamos que f(x) es la función a la que siguen nuestros datos dados. Construiremos algunos modelos que se pueden denotar como 
. Cada punto de esta función es una variable aleatoria que tiene un número de valores igual al número de modelos. Para aproximar correctamente la verdadera función f(x), tomamos el valor esperado de
![f\hat(x) : E[f\hat(x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-59696a64c6219ee148234539345cef2f_l3.png "Rendered by QuickLaTeX.com")
Bias :Variance :
![E[f^2\hat] - E[f\hat]] = E[(f\hat - E[f\hat])^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7c29128c7af841ae3b5de2affdd37ac6_l3.png "Rendered by QuickLaTeX.com")
Veamos algunas imágenes de la importancia que tienen estos dos términos.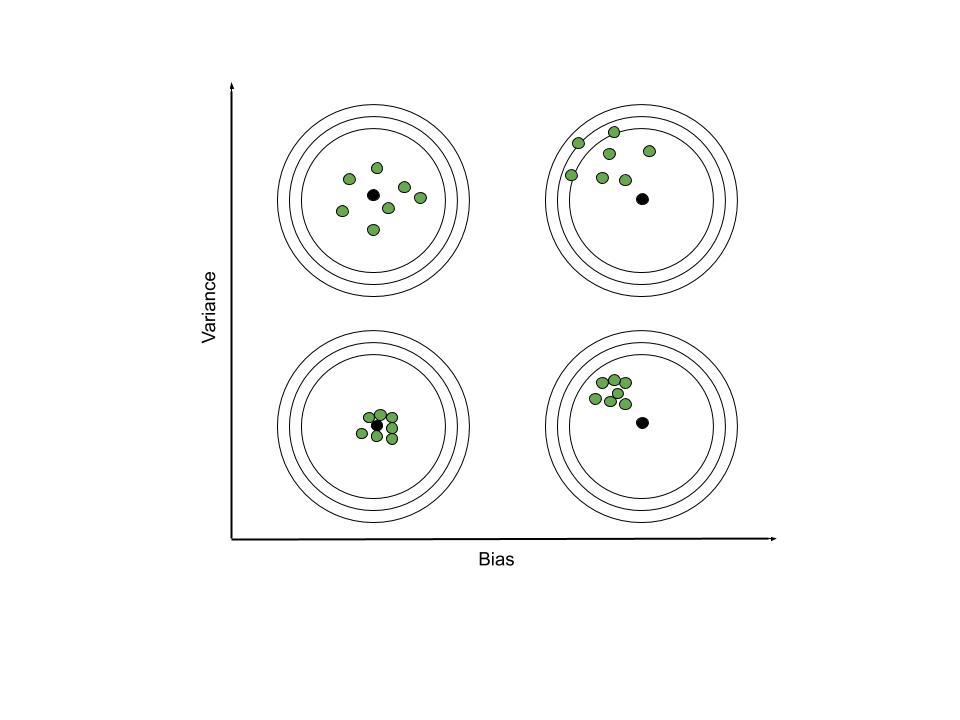
Estas imágenes se explican por sí mismas. Aún así, hablaremos de las cosas a tener en cuenta. Cuando el sesgo es alto, el punto focal del grupo de función predicha se encuentra lejos de la función real. Mientras que, cuando la varianza es alta, las funciones del grupo de las predichas difieren mucho entre sí.
Tomemos un ejemplo en el contexto del aprendizaje automático. Los datos tomados aquí siguen la función cuadrática de las características (x) para predecir la columna de destino (y_noisy). En escenarios de la vida real, los datos contienen información ruidosa en lugar de valores correctos. Por lo tanto, hemos agregado 0 ruido gaussiano de media y 1 de varianza a los valores de la función cuadrática.
| X | y | y_ruidoso |
|---|---|---|
| -5 | 25 | 2.67595670e+01 |
| -4.5 | 20.25 | 2.11632561e+01 |
| -4 | dieciséis | 1.46802434e+01 |
| -3.5 | 12.25 | 1.31647290e+01 |
| -3 | 9 | 1.05460668e+01 |
| -2.5 | 6.25 | 5.95794282e+00 |
| -2 | 4 | 3.25487498e+00 |
| -1.5 | 2.25 | 1.97478968e+00 |
| -1 | 1 | 1.73960283e+00 |
| -0.5 | 0.25 | -1.13112086e-02 |
| 0 | 0 | 1.64552536e+00 |
| 0.5 | 0.25 | -9.60938656e-01 |
| 1 | 1 | 4.46816845e-01 |
| 1.5 | 2.25 | 4.01016081e+00 |
| 2 | 4 | 1.54342469e+00 |
| 2.5 | 6.25 | 7.27654456e+00 |
| 3 | 9 | 9.37684917e+00 |
| 3.5 | 12.25 | 1.32076198e+01 |
| 4 | dieciséis | 1.79133242e+01 |
| 4.5 | 20.25 | 2.08601281e+01 |
Visualización de datos
Ahora que tenemos un problema de regresión, intentemos ajustar varios modelos polinómicos de diferente orden. Los resultados aquí presentados son de grado: 1, 2, 10.
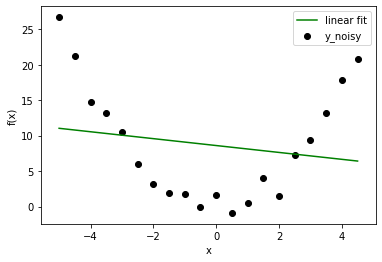
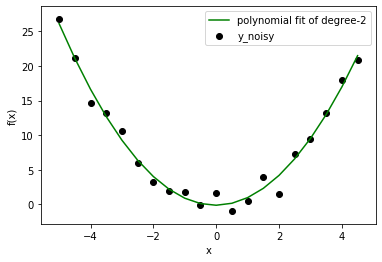
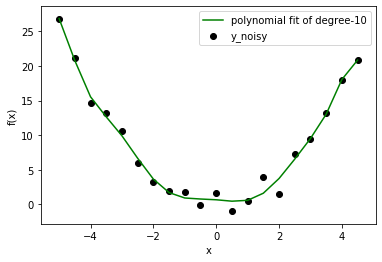
En este caso, ya sabemos que el modelo correcto es de grado=2. Pero tan pronto como amplíe su visión de un problema de juguetes, se enfrentará a situaciones en las que no conoce la distribución de datos de antemano. Por lo tanto, si elige un modelo con un grado más bajo, es posible que no ajuste correctamente el comportamiento de los datos (deje que los datos estén lejos del ajuste lineal). Si elige un grado más alto, quizás esté ajustando ruido en lugar de datos. De todos modos, el modelo de grado inferior le dará un error alto, pero el modelo de grado superior aún no es correcto con un error bajo. ¿Entonces, qué debemos hacer? Podemos usar el método de Visualización o podemos buscar una mejor configuración con Sesgo y Varianza. (Los científicos de datos usan solo una parte de los datos para entrenar el modelo y luego usan el resto para verificar el comportamiento generalizado).
Ahora, si trazamos un conjunto de modelos para calcular el sesgo y la varianza de cada modelo polinomial:
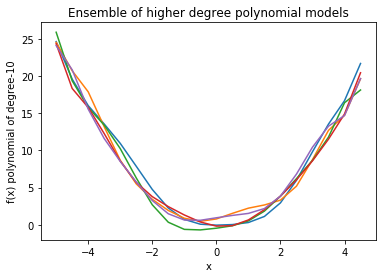
As we can see, in linear model, every line is very close to one another but far away from actual data. On the other hand, higher degree polynomial curves follow data carefully but have high differences among them. Therefore, bias is high in linear and variance is high in higher degree polynomial. This fact reflects in calculated quantities as well.
Linear Model:- Bias : 6.3981120643436356 Variance : 0.09606406047494431 Higher Degree Polynomial Model:- Bias : 0.31310660249287225 Variance : 0.565414017195101
Después de esta tarea, podemos concluir que el modelo simple tiende a tener un sesgo alto mientras que el modelo complejo tiene una varianza alta. Podemos determinar el ajuste insuficiente o el ajuste excesivo con estas características.
Volviendo a la parte matemática: cómo se relacionan el sesgo y la varianza con el error empírico (MSE, que no es un error verdadero debido al ruido agregado en los datos) entre el valor objetivo y el valor predicho.
![\begin{align*} MSE =& E[(f-f\hat)^2]\\ =& E[f^2 - 2ff\hat + f\hat^2]\\ =& f^2E[1] - 2fE[f\hat] + E[f\hat^2]\\ =& f^2 - 2fE[f\hat] + E[f\hat^2]\\ \end{align*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5006891330ab316cc57df0f450b50ac9_l3.png "Rendered by QuickLaTeX.com")
Ahora, calculemos otra cantidad:
![\begin{align*} bias^2 + variance =& (f-E[f\hat])^2 + E[f\hat^2] - {(E[f\hat])}^2\\ =& f^2 - 2fE[f\hat] + (E[f\hat])^2 + E[f\hat^2] - (E[f\hat])^2\\ =& f^2 - 2fE[f\hat] +E[f\hat^]\\ =& MSE \end{align*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2fc3956eabf5c4ca58269f6d72cc3abf_l3.png "Rendered by QuickLaTeX.com")
Ahora, llegamos a la fase de conclusión. Lo importante para recordar es que el sesgo y la varianza tienen una compensación y, para minimizar el error, debemos reducir ambos. Esto significa que queremos que la predicción de nuestro modelo esté cerca de los datos (sesgo bajo) y garantizar que los puntos predichos no varíen mucho con el ruido cambiante (varianza baja).