Pregunta 1. Forme el par de ecuaciones lineales en los siguientes problemas y encuentre sus soluciones gráficamente.
(i) 10 estudiantes de la Clase X tomaron parte en una prueba de Matemáticas. Si el número de niñas es 4 más que el número de niños, encuentre el número de niños y niñas que participaron en la prueba.
Solución:
Echemos,
Número de niñas = x
Número de niños = y
Según las condiciones dadas,
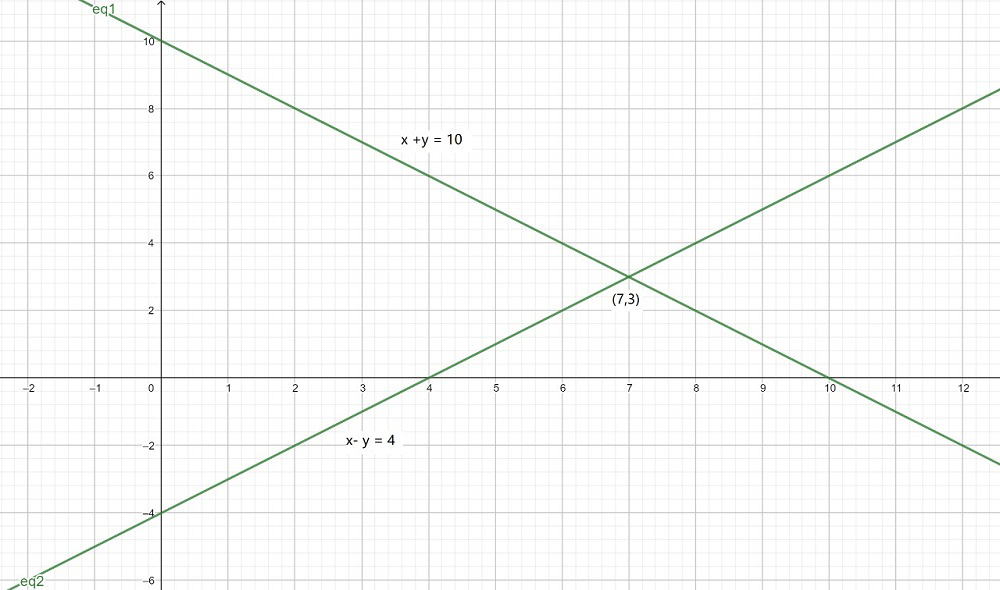
x + y = 10 -(1)
x – y = 4 -(2)
Entonces, para construir un gráfico, necesitamos encontrar al menos dos soluciones de la ecuación dada.
Para la ecuación (1)
x + y = 10, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 10 10 0 Para la ecuación (2)
x – y = 4, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 -4 4 0 El gráfico será el siguiente para la Ecuación (1) y (2):
Ahora, del gráfico, podemos concluir que las líneas dadas se intersecan entre sí en el punto (7, 3).
Por lo tanto, el número de niñas es 7 y el número de niños es 3 en una clase.
(ii) 5 lápices y 7 bolígrafos juntos cuestan ₹ 50, mientras que 7 lápices y 5 bolígrafos juntos cuestan ₹ 46. Halla el costo de un lápiz y el de un bolígrafo.
Solución:
Echemos,
Costo de un lápiz = x
Costo de un lápiz = y
Según las condiciones dadas,
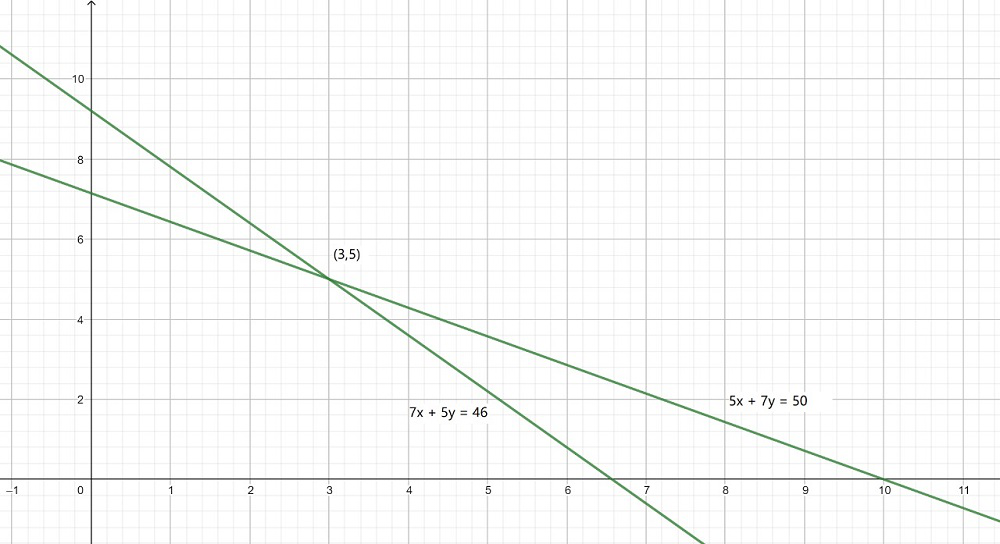
5x + 7y = 50 -(1)
7x + 5y = 46 -(2)
Entonces, para construir un gráfico, necesitamos encontrar al menos dos soluciones de la ecuación dada.
Para la ecuación (1)
5x + 7y = 50, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 3 5 10 0 Para la ecuación (2)
7x + 5y = 46, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 3 5 8 -2 El gráfico será el siguiente para la Ecuación (1) y (2):
Ahora, del gráfico, podemos concluir que las líneas dadas se intersecan entre sí en el punto (3, 5).
Por lo tanto, el costo de un lápiz es ₹ 3 y el costo de un bolígrafo es ₹ 5.
Pregunta 2. Al comparar las razones  , y
, y  , averigua si las rectas que representan los siguientes pares de ecuaciones lineales se cortan en un punto, son paralelas o coincidentes:
, averigua si las rectas que representan los siguientes pares de ecuaciones lineales se cortan en un punto, son paralelas o coincidentes:
(i) 5x – 4y + 8 = 0; 7x + 6y – 9 = 0
Solución:
En las ecuaciones dadas,
a1 = 5
a2 = 7
b1 = -4
b2 = 6
c1 = 8
c2 = -9
En ningún lugar
a1/a2 = 5/7
b1/b2 = -4/6 = -2/3
c1/c2 = 8/-9
Como aquí
Por lo tanto, los pares de ecuaciones dados tienen una solución única y las líneas se intersecan exactamente en un punto.
(ii) 9x + 3y + 12 = 0; 18x + 6y + 24 = 0
Solución:
En las ecuaciones dadas,
a1 = 9
a2 = 18
b1 = 3
b2 = 6
c1 = 12
c2 = 24
En ningún lugar
a1/a2 = 9/18 = 1/2
b1/b2 = 3/6 = 1/2
c1/c2 = 12/24 = 1/2
Como aquí
Por lo tanto, los pares de ecuaciones dados tienen infinitas soluciones y las rectas son coincidentes.
(iii) 6x – 3y + 10 = 0; 2x – y + 9 = 0
Solución:
En las ecuaciones dadas,
a1 = 6
a2 = 2
b1 = -3
b2 = -1
c1 = 10
c2 = 9
En ningún lugar
a1/a2 = 6/2 = 3
b1/b2 = -3/-1 = 3
c1/c2 = 10/9
Como aquí
Por lo tanto, los pares de ecuaciones dados no tienen solución y las líneas son paralelas y nunca se intersecan entre sí.
Pregunta 3. Al comparar las razones  , y
, y  , averigua si el siguiente par de ecuaciones lineales son consistentes o inconsistentes.
, averigua si el siguiente par de ecuaciones lineales son consistentes o inconsistentes.
(i) 3x + 2y = 5; 2x – 3y = 7
Solución:
En las ecuaciones dadas,
a1 = 3
a2 = 2
b1 = 2
b2 = -3
c1 = -5
c2 = -7
En ningún lugar
a1/a2 = 3/2
b1/b2 = 2/-3
c1/c2 = -5/-7
Como aquí
Por lo tanto, los pares de ecuaciones dados tienen una solución única y las líneas se intersecan exactamente en un punto.
Par de ecuaciones lineales son CONSISTENTES.
(ii) 2x – 3y = 8; 4x – 6y = 9
Solución:
En las ecuaciones dadas,
a1 = 2
a2 = 4
b1 = -3
b2 = -6
c1 = -8
c2 = -9
En ningún lugar
a1/a2 = 2/4 = 1/2
b1/b2 = -3/-6 = 1/2
c1/c2 = -8/-9 = 8/9
Como aquí
Por lo tanto, los pares de ecuaciones dados no tienen solución y las líneas son paralelas y nunca se intersecan entre sí.
Un par de ecuaciones lineales son INCONSISTENTES.
(iii) 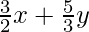 = 7; 9x – 10y = 14
= 7; 9x – 10y = 14
Solución:
En las ecuaciones dadas,
a1 = 3/2
a2 = 9
b1 = 5/3
b2 = -10
c1 = -7
c2 = -14
En ningún lugar
c1/c2 = -7/-14 = 1/2
Como aquí
Por lo tanto, los pares de ecuaciones dados tienen una solución única y las líneas se intersecan exactamente en un punto.
Par de ecuaciones lineales son CONSISTENTES.
(iv) 5x – 3y = 11; – 10x + 6y = –22
Solución:
En las ecuaciones dadas,
a1 = 5
a2 = -10
b1 = -3
b2 = 6
c1 = -11
c2 = 22
En ningún lugar
a1/a2 = 5/-10 = -1/2
b1/b2 = -3/6 = -1/2
c1/c2 = -11/22 = -1/2
Como aquí
Por lo tanto, los pares de ecuaciones dados tienen infinitas soluciones y las rectas son coincidentes.
Par de ecuaciones lineales son CONSISTENTES.
(v) 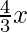 + 2y = 8; 2x + 3y = 12
+ 2y = 8; 2x + 3y = 12
Solución:
En las ecuaciones dadas,
a1 = 4/3
a2 = 2
b1 = 2
b2 = 3
c1 = -8
c2 = -12
En ningún lugar
b1/b2 = 2/3
c1/c2 = -8/-12 = 2/3
Como aquí
Por lo tanto, los pares de ecuaciones dados tienen infinitas soluciones y las rectas son coincidentes.
Par de ecuaciones lineales son CONSISTENTES.
Pregunta 4. ¿Cuáles de los siguientes pares de ecuaciones lineales son consistentes/inconsistentes? Si es consistente, obtenga la solución gráficamente:
(yo) x + y = 5, 2x + 2y = 10
Solución:
En las ecuaciones dadas,
a1 = 1
a2 = 2
b1 = 1
b2 = 2
c1 = -5
c2 = -10
En ningún lugar
a1/a2 = 1/2
b1/b2 = 1/2
c1/c2 = -5/-10 = 1/2
Como aquí
Por lo tanto, los pares de ecuaciones dados tienen infinitas soluciones y las rectas son coincidentes.
Par de ecuaciones lineales son CONSISTENTES.
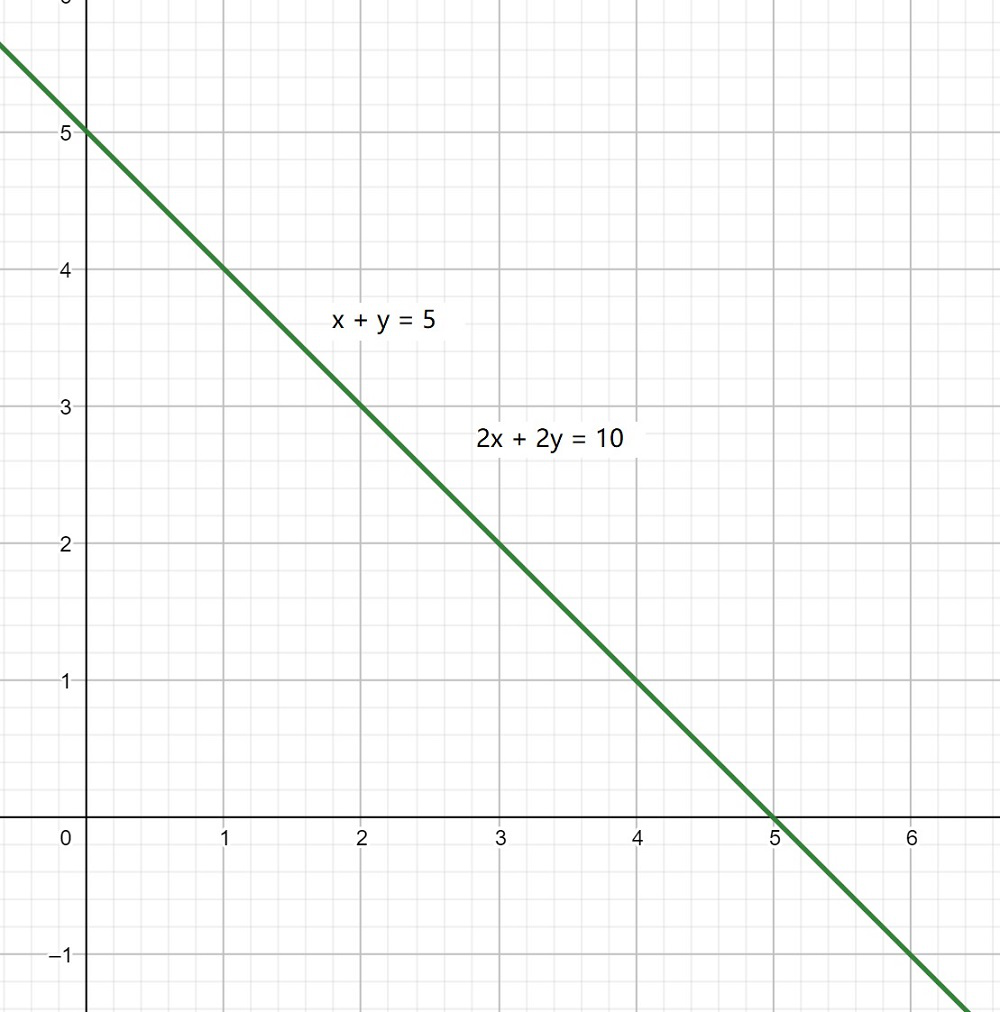
x + y = 5 -(1)
2x + 2y = 10 -(2)
Entonces, para construir un gráfico, necesitamos encontrar al menos dos soluciones de la ecuación dada.
Para la ecuación (1)
x + y = 5, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 5 5 0 Para la ecuación (2)
2x + 2y = 10, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 5 5 0 El gráfico será el siguiente para la Ecuación (1) y (2):
(ii) x – y = 8, 3x – 3y = 16
Solución:
En las ecuaciones dadas,
a1 = 1
a2 = 3
b1 = -1
b2 = -3
c1 = -8
c2 = -16
En ningún lugar
a1/a2 = 1/3
b1/b2 = 1/3
c1/c2 = -8/-16 = 1/2
Como aquí
Por lo tanto, los pares de ecuaciones dados no tienen solución y las líneas son paralelas y nunca se intersecan entre sí.
Un par de ecuaciones lineales son INCONSISTENTES.
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
Solución:
En las ecuaciones dadas,
a1 = 2
a2 = 4
b1 = 1
b2 = -2
c1 = -6
c2 = -4
En ningún lugar
a1/a2 = 2/4 = 1/2
b1/b2 = 1/-2
c1/c2 = -6/-4 = 3/2
Como aquí
Por lo tanto, los pares de ecuaciones dados tienen una solución única y las líneas se intersecan exactamente en un punto.
Par de ecuaciones lineales son CONSISTENTES.
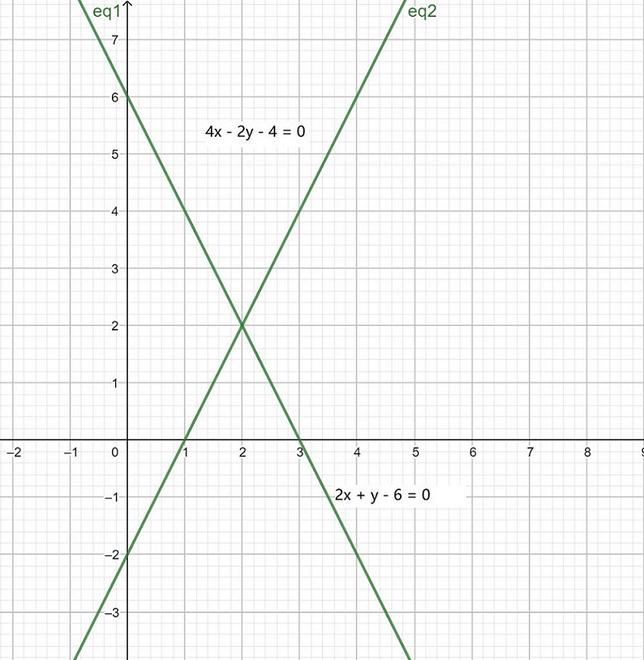
2x + y – 6 = 0 -(1)
4x – 2y – 4 = 0 -(2)
Entonces, para construir un gráfico, necesitamos encontrar al menos dos soluciones de la ecuación dada.
Para la ecuación (1)
2x + y – 6 = 0, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 6 3 0 Para la ecuación (2)
4x – 2y – 4 = 0, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 -2 1 0 El gráfico será el siguiente para la Ecuación (1) y (2):
Ahora, del gráfico, podemos concluir que las líneas dadas se intersecan en el punto (2, 2).
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Solución:
En las ecuaciones dadas,
a1 = 2
a2 = 4
b1 = -2
b2 = -4
c1 = -2
c2 = -5
En ningún lugar
a1/a2 = 2/4 = 1/2
b1/b2 = -2/-4 = 1/2
c1/c2 = -2/-5 = 2/5
Como aquí
Por lo tanto, los pares de ecuaciones dados no tienen solución y las líneas son paralelas y nunca se intersecan entre sí.
Un par de ecuaciones lineales son INCONSISTENTES.
Pregunta 5. La mitad del perímetro de un jardín rectangular, cuyo largo es 4 m más que su ancho, es de 36 m. Encuentra las dimensiones del jardín.
Solución:
Echemos,
longitud = x
ancho = y
La mitad del perímetro de un jardín rectangular =
= x + y
Según las condiciones dadas,
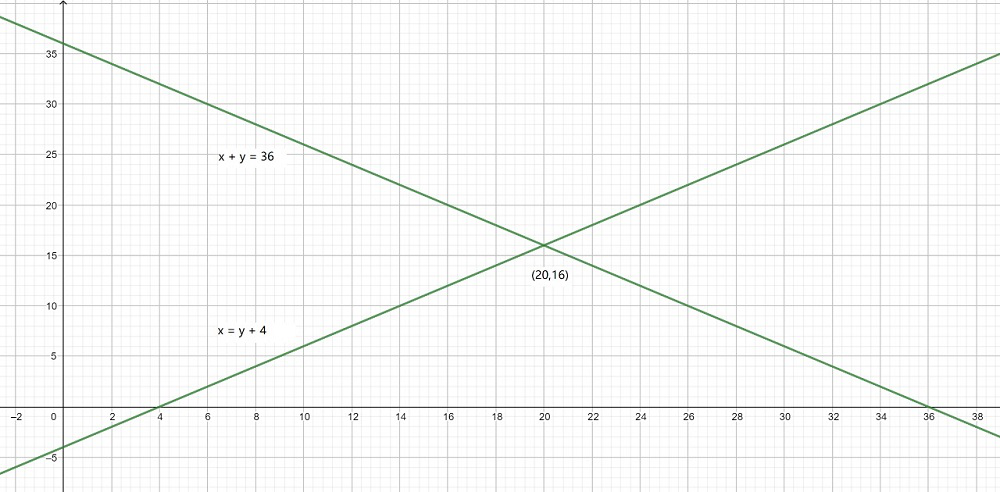
x = y + 4 -(1)
x + y = 36 -(2)
Entonces, para construir un gráfico, necesitamos encontrar al menos dos soluciones de la ecuación dada.
Para la ecuación (1)
x = y + 4, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 -4 4 0 Para la ecuación (2)
x + y = 36, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 36 36 0 El gráfico será el siguiente para la Ecuación (1) y (2):
Ahora, del gráfico, podemos concluir que las líneas dadas se intersecan en el punto (20, 16).
Por lo tanto, la longitud es de 20 my el aliento es de 16 m de rectángulo.
Pregunta 6. Dada la ecuación lineal 2x + 3y – 8 = 0, escribe otra ecuación lineal en dos variables tal que la representación geométrica del par así formado sea:
(i) líneas que se cruzan
Solución:
Ecuación lineal en dos variables tal que el par así formado son líneas que se cruzan, por lo que debe satisfacer las condiciones dadas
Reordenando, obtenemos
Por lo tanto, la ecuación requerida no debe estar en una proporción de 2/3
Por lo tanto, otra ecuación puede ser 2x – 9y + 9 = 0
donde la razón es 2/-9
y,
(ii) líneas paralelas
Solución:
Ecuación lineal en dos variables tal que el par así formado son líneas paralelas, por lo que debe satisfacer las condiciones dadas
Reordenando, obtenemos
Por lo tanto, la ecuación requerida a2/b2 debe estar en una proporción de 2/3 y b2/c2 no debe ser igual a 3/-8
Por lo tanto, otra ecuación puede ser 4x + 6y + 9 = 0
donde la relación a2/b2 es 2/3
y,
(iii) líneas coincidentes
Solución:
Ecuación lineal en dos variables tal que el par así formado son líneas paralelas, por lo que debe satisfacer las condiciones dadas
Reordenando, obtenemos
Por lo tanto, la ecuación requerida a2/b2 debe estar en una proporción de 2/3 y b2/c2 debe ser igual a 3/-8
Por lo tanto, otra ecuación puede ser 4x + 6y -16 = 0
donde la relación a2/b2 es 2/3
y, b2/c2 = 3/-8
Pregunta 7. Dibuja las gráficas de las ecuaciones x – y + 1 = 0 y 3x + 2y – 12 = 0. Determina las coordenadas de los vértices del triángulo formado por estas líneas y el eje x, y sombrea la región triangular.
Solución:
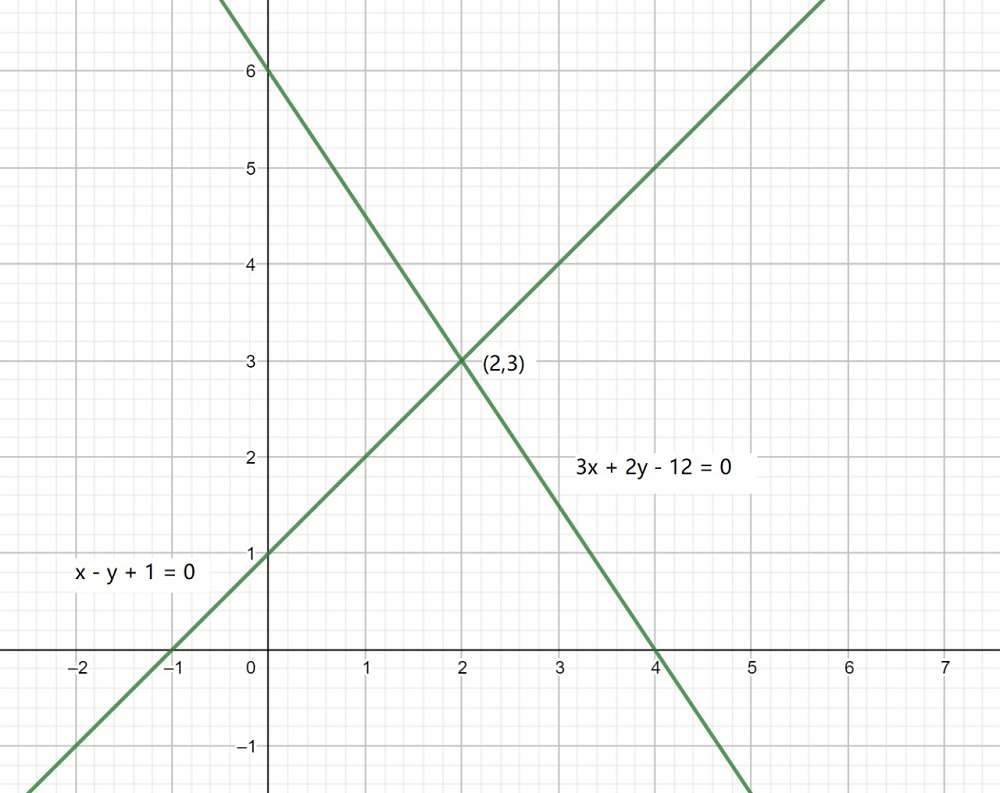
x – y + 1 = 0 -(1)
3x + 2y – 12 = 0 -(2)
Entonces, para construir un gráfico, necesitamos encontrar al menos dos soluciones de la ecuación dada.
Para la ecuación (1)
x – y + 1 = 0, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 -1 1 0 Para la ecuación (2)
3x + 2y – 12 = 0, Entonces, podemos usar la siguiente tabla para dibujar el gráfico:
X y 0 6 4 0 El gráfico será el siguiente para la Ecuación (1) y (2):
Ahora, del gráfico, podemos concluir que las líneas dadas se intersecan entre sí en el punto (2, 3) y el eje x en (−1, 0) y (4, 0).
Por lo tanto, los vértices del triángulo son (2, 3), (−1, 0) y (4, 0).