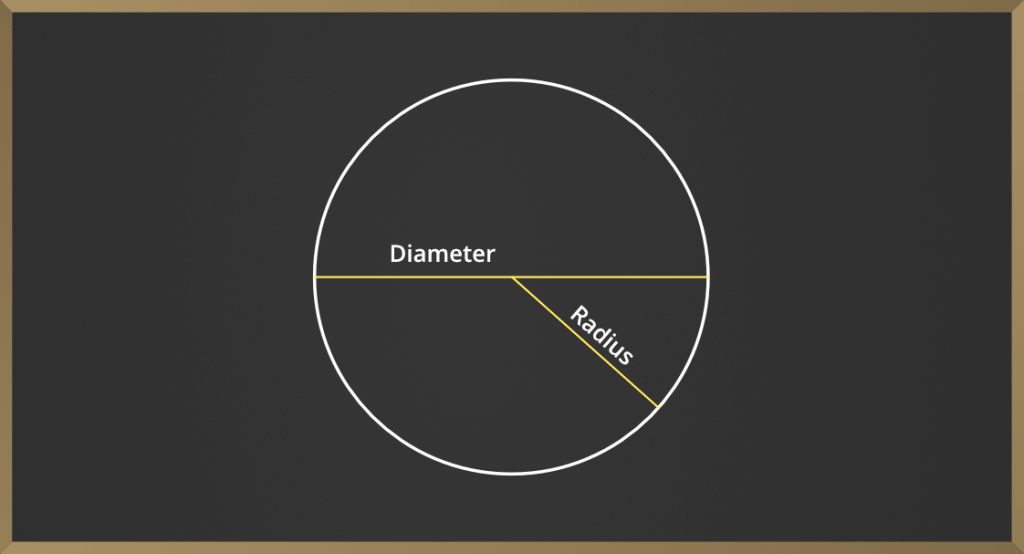
Un círculo es una forma que consiste en una línea curva completamente rodeada por un área. El círculo contiene puntos en el plano que están a la distancia dada de un punto dado, el centro, equivalentemente a la curva trazada por un punto que se mueve en un plano por lo que la distancia desde un punto dado es constante. La distancia entre cualquier punto y el centro del círculo se llama radio (r).

área de un círculo
El área del círculo se calcula con la fórmula:
r 2 _
- r es el radio del círculo.
- π es la relación entre el diámetro de un círculo y su circunferencia
- El valor π es 22/7 (o) 3,14.
Circunferencia de un círculo
El perímetro del círculo es la distancia a lo largo del límite del círculo. El perímetro también se llama la circunferencia de un círculo. La circunferencia será el π por el diámetro del círculo.
- La circunferencia de un círculo es 2 π r .
Ángulo de Sector y Arco
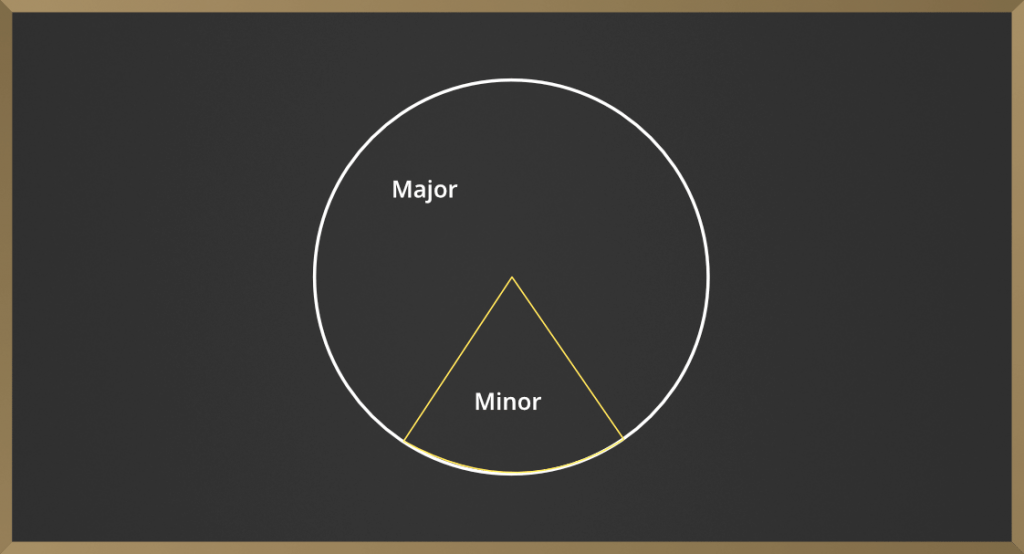
Sector
Un sector de un círculo se define como la región de un círculo encerrada por un arco y dos radios (r). El área más pequeña de un círculo se llama sector menor y el área más grande de un círculo se llama sector mayor.
Ángulo de un Sector
- El ángulo de un sector es aquel ángulo que está encerrado entre los dos radios del sector. Consiste en un arco.
- Un sector que tiene un ángulo central de 180° se conoce como semicírculo.
- Un arco menor es más pequeño que un semicírculo. Un ángulo central que está subtendido por un arco menor tiene una medida de menos de 180°.
- Un arco mayor es más grande que un semicírculo. Un ángulo central subtendido por un arco mayor tiene una medida mayor de 180°.
Arco
- Para encontrar la longitud de un arco de círculo usamos la fórmula de longitud de arco: longitud = radio * θ
- Un arco es una parte de una curva.
- Es una porción de la circunferencia del círculo.

Problemas de muestra
Problema 1: Hallar el área de un sector y la longitud de arco de una circunferencia de radio
4cm y el ángulo central es 2 π /5.
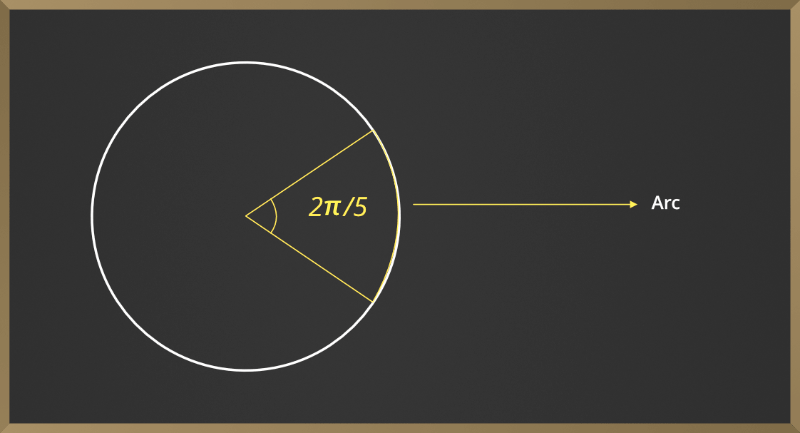
Solución:
Longitud de arco, l = 4*2π/5
= 8π//5cm.
área de un sector = 1/2θr2
= 1/2 * 2π/5 *42
= 16π/5cm2.
Circunferencia de un círculo cuando se da el área
La circunferencia del círculo se puede referir como la distancia lineal a su alrededor. Si el círculo se abre para formar una línea recta, la longitud de esa línea será la circunferencia s del círculo.
Para calcular la circunferencia de un círculo dado, necesitamos multiplicar el diámetro del círculo con el π.
Problema 2: ¿Cuál es el perímetro del círculo cuya superficie es de 314,159 cm2

Solución:
La fórmula del área superficial del círculo, la conocemos:
A = πxr2
Ahora, reemplazando el valor:
314.159 = πxr2
314.159 = 3.14 xr 2
r2 = 314,159/3,14
r2 = 100,05
r = √100.05
r = 10 cm
C = 2 * π * r
Valor de sustitución de r
= 2π * 10
= 2 * 3.14 * 10
= 62,8 cm.
Área de círculo parcial y longitud de arco
El área del círculo también puede denominarse circunferencia . El área del círculo parcial que también se llama sector se puede encontrar mediante la fórmula
[( π *r 2 )/360]θ
La longitud del arco está dada por
(θ/360)*(2 * π * r)
Problema 3: Un círculo de radio 4 unidades, el ángulo de su sector es de 45°. Encuentre el área del sector.
Solución:
Dado,
radio r = 4 unidades
Ángulo θ = 45°
zona del sector
= θ/360 o × πr 2
= 45/360 × 22/7 × 4 2 = 6,28 unidades cuadradas.
Área de una región sombreada
La región sombreada es la región que se puede encontrar cuando una forma se inscribe dentro de la otra forma.
- El área de la región sombreada se puede calcular restando el área del área de la forma inscrita del área de la forma que está inscrita en ella.
- Por ejemplo, supongamos que un círculo está inscrito en el triángulo, entonces el área de la región sombreada es el área del triángulo menos el área del círculo inscrito en el triángulo ( área sombreada = área de un triángulo – área de un círculo ) .
Problema 4: Encuentra el área de la región sombreada.
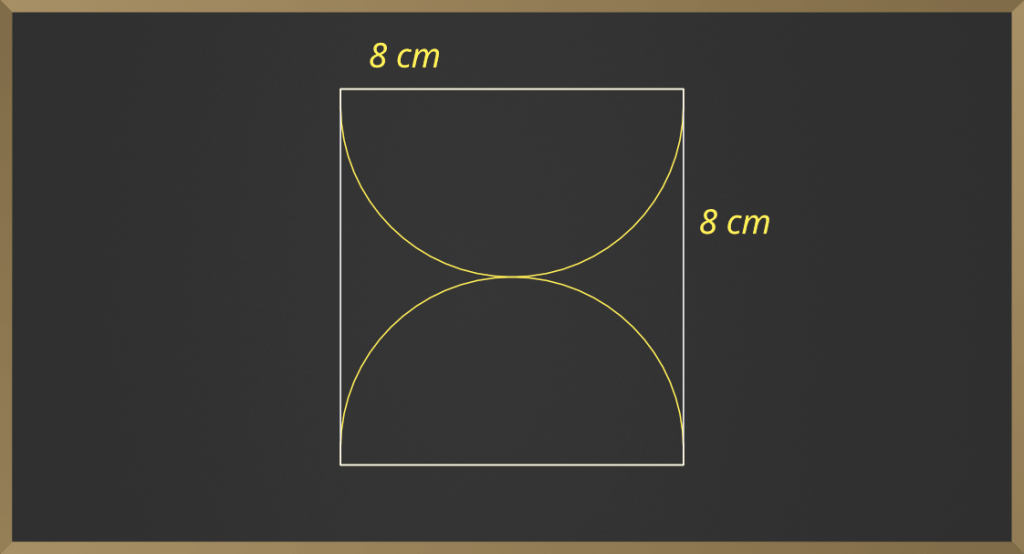
Solución:
El área de la porción sombreada, tenemos que restar el área de dos semicírculos del área del cuadrado
Área de la porción sombreada = Área del cuadrado – (Área del semicírculo + Área de otro semicírculo).
= a2 – [(1/2) πr 2 ) + ((1/2) πr 2 )]
= 82 – πr 2
= 64 – (22/7)⋅ (7/2)2
= 64- (22/7)⋅ (7/2)⋅ (7/2)
= 64 – 38,5
= 25,5 cm2
Problema 5: Encuentra el área de la región sombreada.
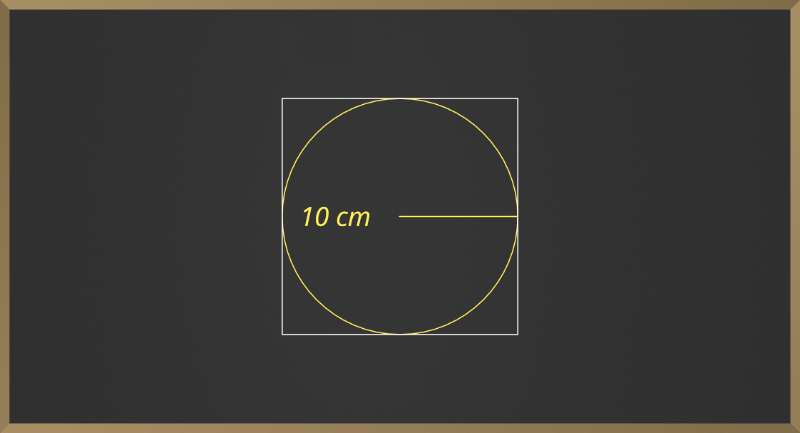
Solución:
Radio dado r = 10 cm
área de la región sombreada = área del cuadrado – área del círculo inscrito dentro del cuadrado.
área del cuadrado= S 2
diámetro del círculo será igual a la longitud del lado del cuadrado por lo que
re = S = 2*10
= 20
area del cuadrado =(20) 2
= 400 cm 2
área del círculo = πr 2
= 3,14 * 10 * 10
= 314 cm2
Área de la región sombreada = área del cuadrado – área del círculo inscrito dentro del cuadrado
= 400 – 314
= 86cm
Por lo tanto, el área de la región sombreada es de 86 cm.
Publicación traducida automáticamente
Artículo escrito por kadiummanisha y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA