Soluciones NCERT de Clase 9 – Capítulo 3 Geometría de coordenadas – Ejercicio 3.3

Pregunta 1: ¿En qué cuadrante o en qué eje se encuentran cada uno de los puntos (– 2, 4), (3, – 1), (– 1, 0), (1, 2) y (– 3, – 5) ? Verifica tu respuesta ubicándolos en el plano cartesiano.

Solución: 

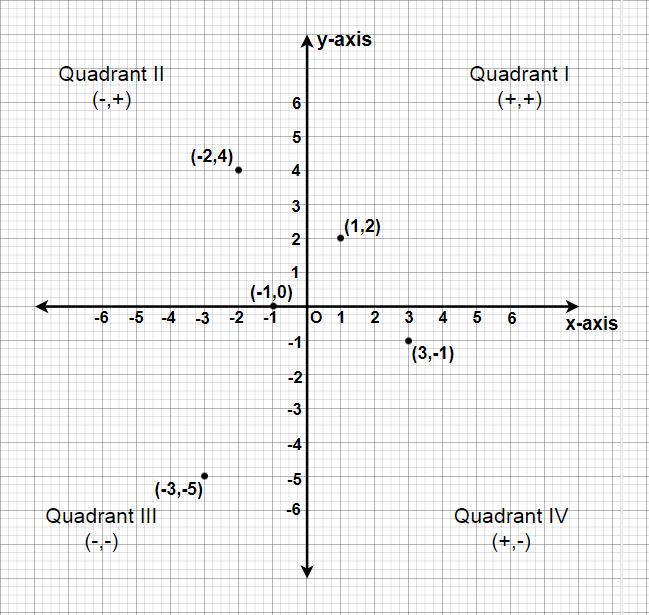
(i) El punto (-2, 4) se encuentra en el ^segundo cuadrante del plano cartesiano, ya que la coordenada x es negativa y la coordenada y es positiva.

(ii) El punto (3, -1) se encuentra en el IV ^cuadrante del plano cartesiano, ya que la coordenada x es positiva y la coordenada y es negativa.

(iii) El punto (-1, 0) se encuentra en el eje x negativo y el valor de la coordenada x es negativo.

(iv) El punto (1, 2) se encuentra en el I ^er Cuadrante en el Cartesiano ya que tanto x como y son positivos.

(v) El punto (-3,-5) se encuentra en el III ^er Cuadrante en el plano cartesiano ya que tanto x como y son negativos.

Pregunta 2: Trace los puntos (x, y) dados en la siguiente tabla en el plano, eligiendo las unidades de distancia adecuadas en los ejes.

Solución:

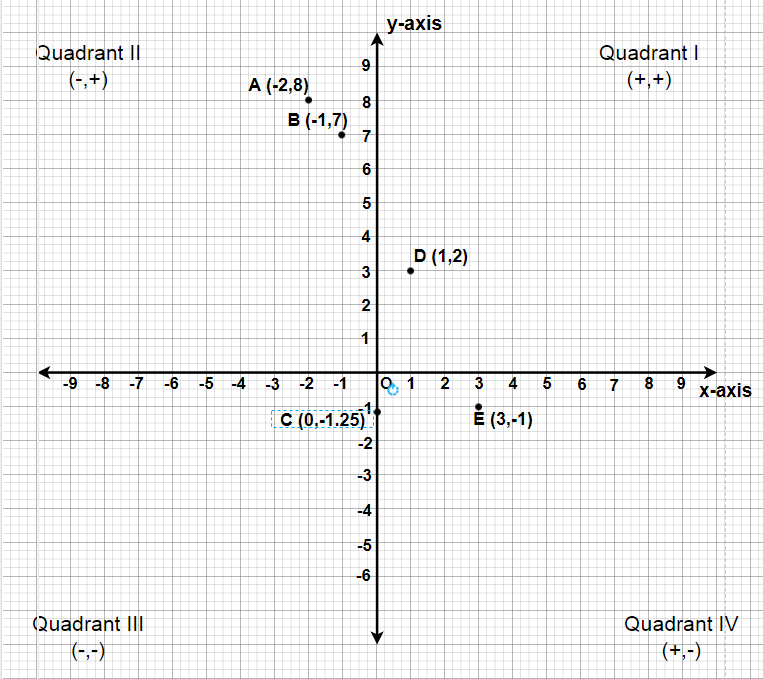
Tenemos que graficar estos puntos A(-2, 8), B(-1, 7), C(0, -1.25), D(1, 3) y E(3, -1).
Pasos que tenemos que usar para trazar estos puntos,

• Que 1 unidad represente 1 cm.
• Para graficar (-2, 8), tomamos (-2) unidades en el eje x y (+8) unidades en el eje y. Ahora podemos graficar A (-2, 8), estará en el cuadrante II.
• Para graficar (-1, 7), tomamos (-1) unidades en el eje x y (+7) unidades en el eje y. Ahora podemos graficar B(-1, 7), estará en el cuadrante II.
• Para graficar (0, -1.25), procederemos (-1.25) unidades debajo del eje x en el eje y y marcaremos la gráfica como C(0, -1.25), estará en el lado negativo de y- eje.
• Para graficar (1, 3), tomamos (+1) unidades en el eje x y (+3) unidades en el eje y. Ahora podemos graficar D(1, 3), estará en el cuadrante-I.
• Para graficar (3, -1), tomamos (+3) unidades en el eje x y (-1) unidades en el eje y. Ahora podemos trazar el punto E(3, -1), estará en el cuadrante IV.