Criterios de semejanza de triángulos

Las cosas a menudo se denominan similares cuando la estructura física o los patrones que muestran tienen propiedades similares. A veces, dos objetos pueden variar en tamaño, pero debido a sus similitudes físicas, se les llama objetos similares. Por ejemplo, un cuadrado más grande siempre será similar a un cuadrado más pequeño. En los Triángulos, si los tamaños varían pero la forma que tienen es parecida, entonces los Triángulos pueden llamarse Triángulos Semejantes. Cuando dos triángulos se declaran Similares, sus ángulos correspondientes son siempre congruentes (Idénticos en forma), y sus lados son Proporcionales. Aprendamos más sobre las similitudes de los triángulos.

Triángulos similares

Dos o más de dos triángulos son semejantes cuando sus ángulos correspondientes son congruentes y sus lados son proporcionales entre sí (la razón de sus lados es igual). Notar cosas de nuestra vida diaria o una buena mirada en nuestros libros de texto nos dice que hay tantos objetos similares entre sí que nunca habíamos notado. Por ejemplo, un oso bebé se parece a su madre aunque la madre es relativamente más grande, la misma. el concepto se aplica aquí en triángulos.

Diferencia entre Triángulos Similares y Triángulos Congruentes

• En Triángulos Similares, la Forma es siempre la misma, pero el Tamaño puede variar.
• En Triángulos Congruentes, tanto la forma como el tamaño son iguales.

ΔABC y ΔPQR son Triángulos congruentes

Teorema de Tales o Teorema de Proporcionalidad Básico

Un famoso matemático griego «Thales» dio un teorema universal para triángulos: «En dos triángulos que son equiángulos (los ángulos correspondientes de ambos triángulos son iguales), la proporción de sus lados correspondientes es siempre igual».

Como podemos notar, los Dos triángulos dados arriba son equiángulos.

∠A = ∠A [Ángulo común]

∠B = ∠D [Ángulos correspondientes]

∠C = ∠E [Ángulos correspondientes]

Por lo tanto, se concluye “Si se traza una recta paralela a un lado del triángulo para que se corte en los dos lados restantes, dividirá los dos lados restantes en la misma proporción”

, DF//BC

Prueba del teorema de Tales

Si se traza una línea paralela a un lado de un triángulo, cortando otros lados en puntos distintos, entonces la división de los otros dos lados está en la misma proporción

Probar: 

Dado: 

En ΔABC, DE es paralela a BC

Construcción:

Una BE y CD y dibuje perpendiculares a AC y AB desde D y E.

Prueba:

En ΔADE, Área del triángulo = 1/2 × DE × EN ⇢ 1

Además, 1/2 × DE × DM ⇢ 2

En ΔBDE, Área del Triángulo =1/2 × BD × EN ⇢ 3

En ΔDEC, Área del Triángulo= 1/2 × EC × DM ⇢ 4

Dividiendo la ecuación 1 y 3

⇢ 5

Dividiendo la ecuación 2 y 4

\ ⇢ 6

Sabemos que el área de ΔBDE y ΔDEC son iguales, ya que BD es paralelo a DE y ambos tienen la misma base DE

Ahora, de la ecuación 5 y 6

Recíproco del teorema de Tales 

Si una recta divide dos lados cualesquiera del triángulo en la misma proporción, entonces la recta es paralela al tercer lado del triángulo.

Prueba:

Dado: 

Construcción:

Supongamos que la línea MN no es paralela a QR. Dibuje otra línea MK tal que MK sea paralela a QR.

Ahora, en ΔPQR, 

⇢ 1

pero, esto también siempre que,

⇢ 2

Pero, K y N se encuentran en la misma línea PR, por lo tanto, coinciden entre sí y son solo el mismo punto.

Por tanto, MN y MK son la misma recta y MN es paralela a QR.

Criterios de semejanza de triángulos

Dos triángulos se llaman similares cuando sus ángulos son iguales y sus lados correspondientes siempre están en la misma proporción, esto es lo que hemos aprendido hasta ahora, sin embargo, no es necesario probar todo lo mencionado anteriormente para demostrar la similitud de dos triángulos. Hay 3 formas más fáciles de averiguar si los dos triángulos son semejantes.

Teorema 1: Criterio de similitud SSS

Establece que si en un triángulo todos los lados son proporcionales a los lados de otros triángulos, entonces los ángulos correspondientes siempre serán iguales y, por lo tanto, ambos triángulos son similares.

Prueba:

Probar: 

Dado: ∠A=∠D, ∠B=∠E, ∠C=∠F

Construcción: Dibuje una línea PQ en ΔDEF tal que AB = DP, AC = DQ, BC = PQ

Prueba: 

Recíproco de la fracción, 

Resta la ecuación por 1 en ambos lados

Por el contrario de BPT, PQ es paralelo a EF

Por lo tanto, ∠P = ∠E, ∠Q = ∠F (por los ángulos correspondientes)

Por lo tanto, ΔDEF∼ ΔDPQ

BC=PQ, AB=DP, AC=DQ

ΔABC≅ ΔDPQ

∠A= ∠D, ∠B= ∠P, ∠C= ∠Q, ∠B= ∠E, ∠C= ∠F,

Por lo tanto, ΔABC ∼ ΔDEF

Teorema 2: Criterio de similitud AAA O AA 

AAA refiriéndose a los ángulos (los tres) de los triángulos. Dice: «Si los dos ángulos correspondientes, ambos triángulos son iguales, entonces sus lados respectivos siempre tendrán la misma proporción y los triángulos son triángulos similares».

AA es otro nombre para el teorema ya que tener dos ángulos iguales automáticamente hará que el tercer ángulo de los triángulos sea igual ya que la suma siempre es 180°.

Prueba:

Dado: ∠A = ∠D, ∠B = ∠E, ∠C = ∠F

Probar: 

Construcción: Haz una línea PQ en ΔDEF tal que AB=DP, AC=DQ, BC=PQ

Prueba: En ΔABC y ΔDPQ 

AB=DP, AC=DQ, ∠A=∠D

Por la propiedad SAS de los triángulos, ambos triángulos son congruentes entre sí.

ΔABC≅ ΔDPQ

Podemos decir, ∠B= ∠DPQ (Por CPCT)

 ∠B= ∠E, por lo tanto ∠E = ∠DPQ 

Por ángulos correspondientes, se puede concluir que PQ es paralelo a EF

Con la ayuda del teorema del inverso de Tales,

Agregar 1 a LHS y RHS

Reemplace DP con AB y DQ con AC

Por lo tanto, la razón de los lados correspondientes también resulta ser igual.

Por lo tanto, ΔABC= ΔDEF

Teorema 3: Criterio de similitud SAS

Si los dos ángulos de ambos triángulos junto con los lados conectados a ellos son iguales, entonces los triángulos se llaman Triángulos similares.

Prueba 

Para probar: ΔABC∼ ΔDEF

Dado: ∠A= ∠D, 

Construcción: Dibujar una línea PQ en el triángulo ΔDEF Tal que AB= DP, AC=DQ

Reciprocar la fracción, 

Restando ambos lados por 1, 

Entonces, PQ es paralelo a EF (a la inversa de BPT)

∠P= ∠E, ∠Q= ∠F (por los ángulos correspondientes)

ΔABC= ΔDPQ

∠A= ∠D, ∠B=∠P, ∠C=∠Q

Como ∠P=∠E, ∠Q= ∠F

Por lo tanto, ∠A=∠D, ∠B= ∠E, ∠C= ∠F

ΔABC∼ ΔDEF

Teorema de Pitágoras

En un triangulo rectangulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados

Prueba:

Dado: ΔPQR es un triángulo rectángulo y QS es perpendicular a PR

Prueba:

Sabemos que, ∠PQR= ∠QSR

∠P= ∠P

Por lo tanto, ΔPQR∼ ΔQSR

QR ² = PR × RS ⇢ 1 

Aplicar lo mismo para Δ PQR y Δ PSQ

PQ ² = PR × PS ⇢ 2

De 1 y 2,

PQ ² + QR ² = PR × RS + PR × PS

PQ ² + QR ² = PR (RS+ PS)

PQ ² + QR ² = PR ²

Por lo tanto, Probado.

Problemas de muestra

Pregunta 1: En la figura que se muestra a continuación, XY es paralelo a BC, AX = 2 cm, XB = 3 cm y la base del triángulo BC = 5 cm. Luego, encuentre el valor de XY usando el Teorema de Tales.

Solución:

Según el teorema de Tales,

 

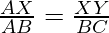
XY = 2cm

Pregunta 2: En el triángulo rectángulo que se muestra a continuación, ¿cuál es el valor de p en términos de q?

Solución:

ABC es un triángulo rectángulo,

Usando el teorema de Pitágoras, obtenemos,

CA ² = AB ² + BC ²

P2 = (4q) ^{2 +} (3q) ²

P2 ⁼ 16q+ 9q

p2 ⁼ 25q

p= 5q

Pregunta 3: En la siguiente figura, cuando PQ es paralela a BC, encuentre el valor de x.

Solución:

En el Triángulo, PQ es paralelo a BC, por lo tanto, se puede aplicar el teorema de Tales,

(3x-3)(2)= (x+2)(5)

6x-6= 5x+ 10

X = 16

Pregunta 4: ¿Cuáles son las tres formas de probar la similitud de Dos Triángulos?

Responder:

Las tres formas de probar la semejanza de triángulos son:

1. Criterio de similitud AAA (ángulo-ángulo-ángulo)
2. Criterio de similitud SAS (lado-ángulo-lado)
3. Criterio de similitud SSS (lado-lado-lado)

Pregunta 5: En el Triángulo ABC, la Línea DE está dibujada de tal manera que ∠ABC = ∠DEC, Demuestra que ΔABC≅ ΔDEC.

Solución: 

En ΔABC y ΔDEC, 

Ya está dado que ∠ABC= ∠DEC

Y como el ángulo C es común en ambos Triángulos, podemos decir, 

∠ACB= ∠DCE

Como dos ángulos son iguales, automáticamente el tercer ángulo será igual ya que la suma de los tres ángulos de un triángulo siempre es 180°

Por lo tanto, a partir del criterio de similitud AAA, se puede concluir,

ΔABC ≅ ΔDEC

Pregunta 6: En un triángulo isósceles de ángulo recto, la base del triángulo mide 2 cm. Encuentra la hipotenusa del triángulo.

Solución:

El Triángulo dado en la pregunta es un triángulo isósceles de ángulo recto y se verá así.

BC= 2cm

Como es un triángulo isósceles, AB= 2cm, 

Según el teorema de Pitágoras, AC ² = AB ² + BC ²

CA ² = 2 ² + 2 ²

CA= √8 = 2√2cm

Pregunta 7: ¿En qué se diferencian SAS y SSS Criterion entre sí?

Responder:

Ambos Criterios tienen el mismo resultado, es decir, ambos probaron que los triángulos son Congruentes entre sí, pero el método para probarlos es muy diferente. En el criterio SSS, cuando se sabe que los tres lados son iguales, entonces los dos Triángulos son de naturaleza Congruente. En el criterio SAS, cuando dos lados cualesquiera y los ángulos entre esos dos lados son iguales, se sabe que los Triángulos son Congruentes.