Número de tangentes desde un punto en un círculo

Un círculo es una colección de todos los puntos en un plano que están a una distancia constante de un punto en particular. Esta distancia se llama radio del círculo y el punto fijo se llama centro. Una línea recta y un círculo pueden coexistir de tres maneras, una puede ser una línea recta sin intersección con la circunferencia del círculo, siempre existe algún espacio entre el círculo y la línea. El segundo tipo es cuando la recta se encuentra de tal manera que pasa tocando la circunferencia de la circunferencia, conocidas como Tangentes de la circunferencia. El tercer tipo es cuando la línea se cruza con la circunferencia en dos lugares y se conoce como secante. Se muestran a continuación,

1. sin intersección
2. Tangente
3. Secante

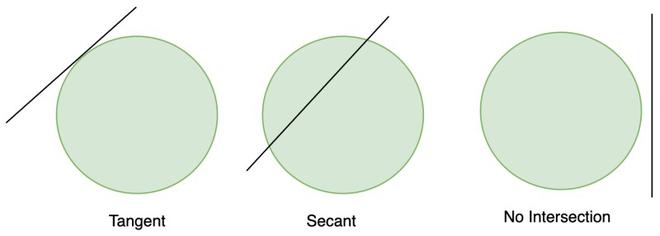
Una secante interseca al círculo en dos puntos, mientras que una tangente interseca en un solo punto. Estudiemos las tangentes y sus propiedades en detalle. 

tangentes

Una línea que corta a un círculo en un solo punto se llama tangente. Un círculo tiene infinitas tangentes posibles. El punto común de la tangente y la circunferencia se llama punto de contacto. 

Veamos algunas propiedades de las tangentes a través de teoremas. 

Número de tangentes de un punto a un círculo 

Ya se sabe que una tangente se define como la recta que pasa tocando la circunferencia de la circunferencia. Para tener una idea de esto, necesitamos realizar algunos experimentos. Hay tres casos que se pueden obtener a través de los diferentes experimentos.

Caso 1: Tangente desde dentro de un Círculo

Intentemos dibujar una tangente desde dentro de un círculo. Supongamos un punto P dentro del círculo e intentemos dibujar tangentes. Observamos que no es posible dibujar tangentes desde el interior del círculo. 

Caso 2: Un punto en el círculo

Podemos ver que en la figura al principio del artículo podemos dibujar una tangente desde cualquier punto del círculo. De hecho, puede haber un número infinito de tangentes en un círculo.

Caso 3: Un punto fuera del círculo

Podemos ver en la figura que desde un punto fuera del círculo, podemos dibujar dos tangentes a él. 

Entonces, para resumir ambos casos:  

1. No hay tangente a un círculo desde un punto dentro del círculo.
2. Hay una tangente a un círculo desde un punto que está en el círculo.
3. Hay dos tangentes posibles a un círculo desde un punto que está fuera del círculo.

Propiedades de las tangentes 

La tangente en cualquier punto de un círculo es perpendicular al radio que pasa por el punto de contacto. 

Prueba: 

Supongamos una circunferencia de centro O y tangente XY a la circunferencia. 

Supongamos cualquier punto Q en la línea XY y unamos el punto de contacto con el centro. El diagrama se verá así, 

Ahora el punto Q cuando se une al centro forma OQ, si se extiende se convertirá en una secante no tangente. Ahora podemos ver que, 

OQ > OP 

Esto es cierto cuando Q es cualquier punto de la línea XY excepto el punto de contacto (P). P es el punto en la línea XY cuya distancia es más corta desde el centro O. Por lo tanto, OP debe ser perpendicular a XY. 

Por lo tanto, Probado. 

Este teorema nos permite concluir algunas otras propiedades también: 

1. En cualquier punto del círculo, solo puede haber una tangente.
2. La línea que une el punto de contacto y el centro es perpendicular a la tangente. Por lo tanto, también se llama normal a la tangente.

Teorema 2: 

Una línea trazada a través del extremo del radio y perpendicular a él es una tangente al círculo. 

Prueba: 

Supongamos un círculo con centro O en el que OP es el radio. Una recta AB pasa por P tal que OP es perpendicular a AB. 

Ahora, tome un punto Q en línea AB. Sabemos que la distancia de Q es la más corta desde O cuando Q = P. En cualquier otro caso,

OQ > OP y Q se encuentra fuera del círculo. Eso significa que AB se encuentra con el círculo en un solo punto P. Por lo tanto, AB es tangente al círculo. 

Pregunta 1: En el diagrama que se muestra a continuación. Se trazan dos tangentes desde un punto exterior que está a 41 cm del centro. El radio del círculo se da como 9 cm. Encuentra el área del cuadrilátero AOBC. 

Solución: 

Sabemos por el teorema anterior que la línea que une el centro desde el punto de contacto es perpendicular a la tangente. Esto hace que OAC y OBC sean triángulos rectángulos. 

Y ahora,

Área del cuadrilátero AOBC = Área del triángulo AOC+ Área del triángulo BOC. 

Área del triángulo AOC = unidades cuadradas.   

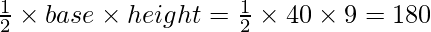
Como ambos triángulos son congruentes, ambos tienen la misma área. Por lo tanto, el área de BOC = 180 unidades cuadradas.

Área del cuadrilátero AOBC = 180 + 180 

                                            = 360 unidades cuadradas. 

Pregunta 2: Supongamos una tangente AB en el punto A del círculo cuyo radio es de 3 cm. La distancia del punto B al centro O es de 5 cm. Halla la longitud de AB. 

Solución: 

Esta es también una aplicación del teorema estudiado anteriormente, primero hagamos un diagrama. 

Podemos ver un triángulo rectángulo AOC aquí,

OC ² = AO ² + AC ² 

52 = 32 + CA ² 

25 = 9 + CA ²

16 = CA ²

CA = 4cm 

Teorema 3: 

Las longitudes de las tangentes dibujadas desde un punto externo a un círculo son iguales.

Prueba: 

Supongamos un círculo con centro O, un punto C fuera del círculo y las tangentes desde ese punto al círculo. AC y BC son las tangentes desde el punto. Nuestro objetivo es probar AC = BC.

Unamos OA y OB y ​​consideremos los dos triángulos OAC y OBC. 

1. El CO es común.
2. ∠OAC = ∠OBC (Triángulo rectángulo)
3. OA = OB (Radios del círculo)

Usando la propiedad RHS podemos decir que estos dos triángulos son congruentes. Por lo tanto, AC = BC. 

Teorema 4: 

Si se trazan dos tangentes desde un punto externo, entonces

1. subtienden un ángulo igual en el centro, y 
2. Están igualmente inclinados al segmento de línea que une el centro con ese punto. 

Prueba:

En la figura dada, tenemos que demostrar que 

∠POA = ∠POB y ∠OPA = ∠OPB.

Consideremos los dos triángulos, POA y POB. 

PA = PB (Por teorema anterior) 

OA = OB (radios del círculo) 

OP = OP (Común) 

Por lo tanto, estos dos triángulos son congruentes. [por SSS] 

Por lo tanto, ∠POA = ∠POB y ∠OPA = ∠OPB.

Problemas de muestra

Pregunta 1: En la figura dada, AC y BC son las dos tangentes trazadas desde el punto C. Demuestra que 2∠OAB = ∠ACB.

Solución: 

Sabemos por el teorema anterior que, AC = BC. Esto concluye que el triángulo ABC es un triángulo isósceles. 

También sabemos que ∠OAC = 90°. Asi que, 

∠BAC = 90° – ∠OAB

En el triangulo BAC

∠BAC+ ∠ABC+ ∠ACB = 180°

2∠BAC+ ∠ACB = 180°

2(90° – ∠OAB) + ∠ACB = 180°

180° – 2∠OAB + ∠ACB = 180°

∠ACB = 2∠OAB 

Pregunta 2: Hay una circunferencia inscrita en un cuadrilátero PQRS, prueba que PQ + RS = PS + QR. 

Solución: 

Un círculo está inscrito dentro del cuadrilátero PQRS. Observa que los lados del cuadrilátero son en realidad tangentes al círculo. 

PA = PB, 

BQ = control de calidad 

RD = CR 

SA = DE 

Necesitamos probar PQ + RS = PS + QR.

Tomando el LHS, 

PQ + RS 

⇒ PB + BQ + DR + DS 

⇒ PA + CQ + RC+ AS (De las relaciones expuestas anteriormente)

⇒ (PA + AS) + (CQ + RC) 

⇒ PD + QR 

Por lo tanto probado

Pregunta 3: En círculos concéntricos, demuestre que la cuerda del círculo mayor que toca al círculo menor se biseca en el punto de contacto. 

Responder: 

Digamos que C ₁ y C ₂ son dos círculos concéntricos. El centro es O y AB es la cuerda del círculo más grande. De los teoremas anteriores sabemos que OP es perpendicular a AB. Como sabemos por las propiedades del círculo, esa perpendicular desde el centro biseca la cuerda. 

AB es cuerda al círculo mayor C ₁ y OP es perpendicular a él. Así se biseca la cuerda.