Uniform-Cost Search es una variante del algoritmo de Dijikstra . Aquí, en lugar de insertar todos los vértices en una cola de prioridad, insertamos solo la fuente, luego insertamos uno por uno cuando sea necesario. En cada paso, verificamos si el elemento ya está en la cola de prioridad (usando la array visitada). En caso afirmativo, ejecutamos la tecla de disminución, de lo contrario, la insertamos.
Esta variante de Dijkstra es útil para gráficos infinitos y aquellos gráficos que son demasiado grandes para representarlos en la memoria. La búsqueda de costo uniforme se utiliza principalmente en inteligencia artificial.
Ejemplos:
Input :
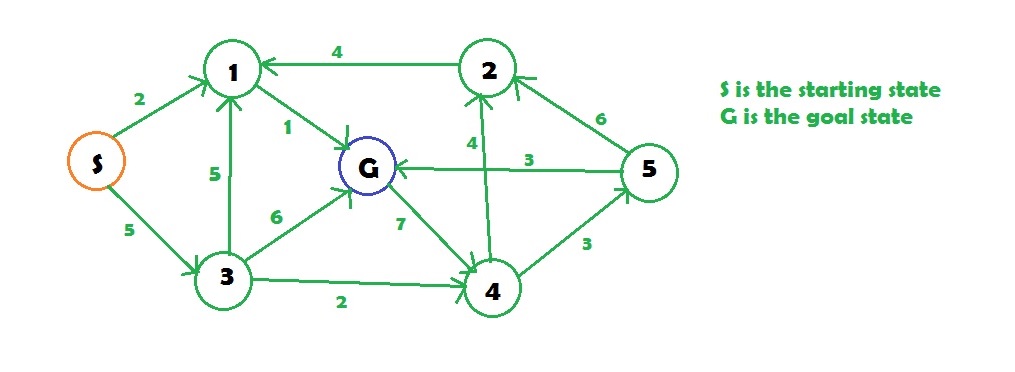
Output : Minimum cost from S to G is =3
La búsqueda de costo uniforme es similar al algoritmo de Dijikstra. En este algoritmo desde el estado inicial, visitaremos los estados adyacentes y elegiremos el estado menos costoso, luego elegiremos el siguiente estado menos costoso de todos los estados no visitados y adyacentes de los estados visitados, de esta manera intentaremos alcanzar el estado objetivo (tenga en cuenta que no continuaremos el camino a través de un estado objetivo), incluso si alcanzamos el estado objetivo, continuaremos buscando otros caminos posibles (si hay múltiples objetivos). Mantendremos una cola de prioridad que dará el siguiente estado menos costoso de todos los estados adyacentes de los estados visitados.
C++
// C++ implementation of above approach
#include <bits/stdc++.h>
using namespace std;
// graph
vector<vector<int> > graph;
// map to store cost of edges
map<pair<int, int>, int> cost;
// returns the minimum cost in a vector( if
// there are multiple goal states)
vector<int> uniform_cost_search(vector<int> goal, int start)
{
// minimum cost upto
// goal state from starting
// state
vector<int> answer;
// create a priority queue
priority_queue<pair<int, int> > queue;
// set the answer vector to max value
for (int i = 0; i < goal.size(); i++)
answer.push_back(INT_MAX);
// insert the starting index
queue.push(make_pair(0, start));
// map to store visited node
map<int, int> visited;
// count
int count = 0;
// while the queue is not empty
while (queue.size() > 0) {
// get the top element of the
// priority queue
pair<int, int> p = queue.top();
// pop the element
queue.pop();
// get the original value
p.first *= -1;
// check if the element is part of
// the goal list
if (find(goal.begin(), goal.end(), p.second) != goal.end()) {
// get the position
int index = find(goal.begin(), goal.end(),
p.second) - goal.begin();
// if a new goal is reached
if (answer[index] == INT_MAX)
count++;
// if the cost is less
if (answer[index] > p.first)
answer[index] = p.first;
// pop the element
queue.pop();
// if all goals are reached
if (count == goal.size())
return answer;
}
// check for the non visited nodes
// which are adjacent to present node
if (visited[p.second] == 0)
for (int i = 0; i < graph[p.second].size(); i++) {
// value is multiplied by -1 so that
// least priority is at the top
queue.push(make_pair((p.first +
cost[make_pair(p.second, graph[p.second][i])]) * -1,
graph[p.second][i]));
}
// mark as visited
visited[p.second] = 1;
}
return answer;
}
// main function
int main()
{
// create the graph
graph.resize(7);
// add edge
graph[0].push_back(1);
graph[0].push_back(3);
graph[3].push_back(1);
graph[3].push_back(6);
graph[3].push_back(4);
graph[1].push_back(6);
graph[4].push_back(2);
graph[4].push_back(5);
graph[2].push_back(1);
graph[5].push_back(2);
graph[5].push_back(6);
graph[6].push_back(4);
// add the cost
cost[make_pair(0, 1)] = 2;
cost[make_pair(0, 3)] = 5;
cost[make_pair(1, 6)] = 1;
cost[make_pair(3, 1)] = 5;
cost[make_pair(3, 6)] = 6;
cost[make_pair(3, 4)] = 2;
cost[make_pair(2, 1)] = 4;
cost[make_pair(4, 2)] = 4;
cost[make_pair(4, 5)] = 3;
cost[make_pair(5, 2)] = 6;
cost[make_pair(5, 6)] = 3;
cost[make_pair(6, 4)] = 7;
// goal state
vector<int> goal;
// set the goal
// there can be multiple goal states
goal.push_back(6);
// get the answer
vector<int> answer = uniform_cost_search(goal, 0);
// print the answer
cout << "Minimum cost from 0 to 6 is = "
<< answer[0] << endl;
return 0;
}
Python3
# Python3 implementation of above approach
# returns the minimum cost in a vector( if
# there are multiple goal states)
def uniform_cost_search(goal, start):
# minimum cost upto
# goal state from starting
global graph,cost
answer = []
# create a priority queue
queue = []
# set the answer vector to max value
for i in range(len(goal)):
answer.append(10**8)
# insert the starting index
queue.append([0, start])
# map to store visited node
visited = {}
# count
count = 0
# while the queue is not empty
while (len(queue) > 0):
# get the top element of the
queue = sorted(queue)
p = queue[-1]
# pop the element
del queue[-1]
# get the original value
p[0] *= -1
# check if the element is part of
# the goal list
if (p[1] in goal):
# get the position
index = goal.index(p[1])
# if a new goal is reached
if (answer[index] == 10**8):
count += 1
# if the cost is less
if (answer[index] > p[0]):
answer[index] = p[0]
# pop the element
del queue[-1]
queue = sorted(queue)
if (count == len(goal)):
return answer
# check for the non visited nodes
# which are adjacent to present node
if (p[1] not in visited):
for i in range(len(graph[p[1]])):
# value is multiplied by -1 so that
# least priority is at the top
queue.append( [(p[0] + cost[(p[1], graph[p[1]][i])])* -1, graph[p[1]][i]])
# mark as visited
visited[p[1]] = 1
return answer
# main function
if __name__ == '__main__':
# create the graph
graph,cost = [[] for i in range(8)],{}
# add edge
graph[0].append(1)
graph[0].append(3)
graph[3].append(1)
graph[3].append(6)
graph[3].append(4)
graph[1].append(6)
graph[4].append(2)
graph[4].append(5)
graph[2].append(1)
graph[5].append(2)
graph[5].append(6)
graph[6].append(4)
# add the cost
cost[(0, 1)] = 2
cost[(0, 3)] = 5
cost[(1, 6)] = 1
cost[(3, 1)] = 5
cost[(3, 6)] = 6
cost[(3, 4)] = 2
cost[(2, 1)] = 4
cost[(4, 2)] = 4
cost[(4, 5)] = 3
cost[(5, 2)] = 6
cost[(5, 6)] = 3
cost[(6, 4)] = 7
# goal state
goal = []
# set the goal
# there can be multiple goal states
goal.append(6)
# get the answer
answer = uniform_cost_search(goal, 0)
# print the answer
print("Minimum cost from 0 to 6 is = ",answer[0])
# This code is contributed by mohit kumar 29
C#
// C# implementation of above approach
using System;
using System.Collections;
using System.Collections.Generic;
class GFG
{
// graph
static List<List<int>> graph=new List<List<int>>();
// map to store cost of edges
static Dictionary<Tuple<int,int>,int> cost= new Dictionary<Tuple<int,int>,int>();
// returns the minimum cost in a vector( if
// there are multiple goal states)
static List<int> uniform_cost_search(List<int> goal, int start)
{
// minimum cost upto
// goal state from starting
// state
List<int> answer=new List<int>();
// create a priority queue
List<Tuple<int, int> > queue = new List<Tuple<int, int> >();
// set the answer vector to max value
for (int i = 0; i < goal.Count; i++)
answer.Add(int.MaxValue);
// insert the starting index
queue.Add(new Tuple<int,int>(0, start));
// map to store visited node
Dictionary<int, int> visited=new Dictionary<int,int>();
// count
int count = 0;
// while the queue is not empty
while (queue.Count > 0) {
// get the top element of the
// priority queue
Tuple<int, int> q = queue[0];
Tuple<int, int> p = new Tuple<int,int>(-q.Item1,q.Item2);
// pop the element
queue.RemoveAt(0);
// check if the element is part of
// the goal list
if (goal.Contains(p.Item2)) {
// get the position
int index = goal.IndexOf(p.Item2);
// if a new goal is reached
if (answer[index] == int.MaxValue)
count++;
// if the cost is less
if (answer[index] > p.Item1)
answer[index] = p.Item1;
// pop the element
queue.RemoveAt(0);
// if all goals are reached
if (count == goal.Count)
return answer;
}
// check for the non visited nodes
// which are adjacent to present node
if (!visited.ContainsKey(p.Item2))
for (int i = 0; i < graph[p.Item2].Count; i++) {
// value is multiplied by -1 so that
// least priority is at the top
queue.Add(new Tuple<int,int>((p.Item1 + (cost.ContainsKey(new Tuple<int,int>(p.Item2, graph[p.Item2][i])) ? cost[new Tuple<int,int>(p.Item2, graph[p.Item2][i])] : 0))*-1,
graph[p.Item2][i]));
}
// mark as visited
visited[p.Item2] = 1;
}
return answer;
}
// main function
public static void Main(params string []args)
{
// create the graph
graph=new List<List<int>>();
for(int i=0;i<7;i++)
{
graph.Add(new List<int>());
}
// add edge
graph[0].Add(1);
graph[0].Add(3);
graph[3].Add(1);
graph[3].Add(6);
graph[3].Add(4);
graph[1].Add(6);
graph[4].Add(2);
graph[4].Add(5);
graph[2].Add(1);
graph[5].Add(2);
graph[5].Add(6);
graph[6].Add(4);
// add the cost
cost[new Tuple<int,int>(0, 1)] = 2;
cost[new Tuple<int,int>(0, 3)] = 5;
cost[new Tuple<int,int>(1, 6)] = 1;
cost[new Tuple<int,int>(3, 1)] = 5;
cost[new Tuple<int,int>(3, 6)] = 6;
cost[new Tuple<int,int>(3, 4)] = 2;
cost[new Tuple<int,int>(2, 1)] = 4;
cost[new Tuple<int,int>(4, 2)] = 4;
cost[new Tuple<int,int>(4, 5)] = 3;
cost[new Tuple<int,int>(5, 2)] = 6;
cost[new Tuple<int,int>(5, 6)] = 3;
cost[new Tuple<int,int>(6, 4)] = 7;
// goal state
List<int> goal=new List<int>();
// set the goal
// there can be multiple goal states
goal.Add(6);
// get the answer
List<int> answer = uniform_cost_search(goal, 0);
// print the answer
Console.Write("Minimum cost from 0 to 6 is = " + answer[0]);
}
}
// This code is contributed by rutvik_56.
Minimum cost from 0 to 6 is = 3
Complejidad: O( m ^ (1+piso(l/e)))
donde,
m es el número máximo de vecinos que tiene un Node
l es la longitud del camino más corto hacia el estado objetivo
e es el menor costo de un borde
Publicación traducida automáticamente
Artículo escrito por andrew1234 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA