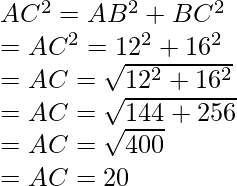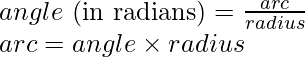Formas inscritas en un círculo: resolución de problemas

En Geometría, hay una clasificación específica donde las formas se encuentran dentro de otras formas, por ejemplo, un círculo dentro de un triángulo, un cuadrilátero dentro de un círculo, etc. Las formas se llaman inscritas y circunscritas . La forma interior se conoce como «formas inscritas», mientras que la forma exterior se conoce como «formas circunscritas». Supongamos que un círculo está inscrito en cualquier otra forma (un polígono), los bordes del polígono (todos tocando el círculo) son las tangentes al círculo.

Triángulos Rectángulos Inscritos en un Círculo 

Cuando un triángulo se inserta en un círculo de tal manera que uno de los lados del triángulo es el diámetro del círculo, entonces el triángulo es un triángulo rectángulo. 

Esto también se conoce como Teorema de Tales .

Prueba:

El siguiente diagrama tiene agregado el segmento de línea OC. 

Como los segmentos OB, OC y OA son radios del mismo círculo, todos son congruentes. Por lo tanto, ambos triángulos COB y COA son triángulos isósceles. Los ángulos B y BCO son congruentes porque son lados opuestos congruentes del triángulo isósceles COB. De manera similar, los ángulos A y ACO son congruentes porque son lados opuestos congruentes del triángulo COA.

La suma de las medidas de los tres ángulos de un triángulo es 180 grados y por tanto,

m(∠A) + m(∠B) + m(∠C) = 180

Usando las equivalencias de ángulos del párrafo anterior

m(∠C) = m(∠BCO) + m(∠ACO)

           = m(∠CBO) + m(∠CAO)

= m(∠B) + m(∠A)

Sustituyendo esto en la fórmula anterior encontramos

2m(∠A) + 2m(∠B) = 180

y entonces m(∠A) + m(∠B) = 90. Dado que las medidas de los tres ángulos del triángulo ABC suman 180, esto significa que m(∠C) = 90° y entonces el triángulo ABC es un triángulo rectángulo como se desea .

Pregunta: El triángulo ΔABC está inscrito en un círculo O, y el lado AC pasa por el centro del círculo. Encuentra el diámetro del círculo.

Responder:

 Sabemos que el triángulo inscrito por una cuerda que pasa por el centro de la circunferencia es un triángulo rectángulo. 

Dado, BC = 16 y AB = 12. 

El teorema de la hipotenusa se puede aplicar aquí, 

El diámetro del círculo es 20. 

Ángulos inscritos en círculos

Un ángulo inscrito en un círculo se define de tal manera que sus dos lados/rayos actúan como la cuerda del círculo y el vértice del ángulo se coloca en la circunferencia del círculo.

Cuando se suma otro ángulo cuyo vértice se sitúa en el centro y los rayos se encuentran con los extremos del ángulo anterior, el ángulo subtendido por el ángulo central se convierte en el doble del ángulo subtendido por el otro ángulo.

Cuadriláteros cíclicos

Cuando un cuadrilátero se inscribe en un Círculo de tal manera que todos los vértices del cuadrilátero tocan la circunferencia del círculo. Hay ciertas propiedades para el cuadrilátero cíclico.

Propiedad: Los ángulos opuestos de un cuadrilátero cíclico siempre suman 180°. O Se puede decir que los ángulos Opuestos son de Naturaleza Suplementaria. 

Aquí, ∠A + ∠C = 180°

 ∠B + ∠D = 180°

Cuando se suman todos los ángulos, ∠A + ∠B + ∠C+ ∠D = 180 + 180 = 360°

Pregunta 1: En la siguiente figura, encuentra el otro ángulo. 

Responder: 

Dado que ambos ángulos inscritos son del mismo arco, los ángulos deben ser iguales. 

Entonces, el otro ángulo también mide 75 ^o

Pregunta 2: En la siguiente figura, encuentre la longitud del arco menor AC. 

Responder:

 Por el teorema estudiado anteriormente, sabemos que el ángulo inscrito en el círculo por un arco es la mitad del ángulo inscrito en el centro por ese mismo arco. Por lo tanto, ∠AOC = 60°. 

Ahora tenemos el ángulo inscrito en el centro y el radio del círculo es de 4 cm (dado). 

La longitud del arco se puede encontrar por

 

30° se da   en radianes. 

Entonces, conectando los valores en la fórmula anterior. 

Entonces, la longitud del arco es 2.0943. 

Pregunta 3: En la figura dada, CD es la cuerda que es igual al radio del círculo, AB es el diámetro como se muestra, las cuerdas AC y BD se extienden fuera del círculo para encontrarse en E. Demuestre que ∠AEB = 60°

Responder: 

Para probar: ∠AEB = 60°

Construcción: Une OC, OD y BC con líneas de puntos.

Prueba: △COD es un triángulo equilátero ya que los tres lados son iguales al radio del círculo.

Entonces, ∠COD= 60° y ∠CBD = 30° (la mitad del ángulo subtendido en el centro)

En △ACB, ∠ACB = 90°

∠BCE= 180-90 (ya que AE es una línea recta) = 90°

En △BCE, ∠BEC+ 90+ 30 = 180°

∠BEC = 60°

Por lo tanto, ∠AEB = 60°