La función de pérdida estima qué tan bien un algoritmo particular modela los datos proporcionados. Las funciones de pérdida se clasifican en dos clases según el tipo de tarea de aprendizaje.
- Modelos de regresión: predecir valores continuos.
- Modelos de clasificación: predecir la salida de un conjunto de valores categóricos finitos.
PÉRDIDAS DE REGRESIÓN
Error cuadrático medio (MSE) / Pérdida cuadrática / Pérdida L2
- Es la media del cuadrado de los residuos para todos los puntos de datos en el conjunto de datos. Los residuos son la diferencia entre la predicción real y la predicha por el modelo.
- El cuadrado de los residuos se realiza para convertir valores negativos en valores positivos. El error normal puede ser tanto negativo como positivo. Si se suman algunos números positivos y negativos, la suma puede ser 0. Esto le indicará al modelo que el error neto es 0 y que el modelo se está desempeñando bien, pero al contrario, el modelo aún se está desempeñando mal. Por lo tanto, para obtener el rendimiento real del modelo, solo se toman valores positivos para obtener valores positivos, se eleva al cuadrado.
- Elevar al cuadrado también da más peso a los errores más grandes. Cuando la función de costo está lejos de su valor mínimo, elevar al cuadrado el error penalizará más al modelo y, por lo tanto, ayudará a alcanzar el valor mínimo más rápido.
- La media del cuadrado de los residuos está tomando en lugar de simplemente tomar la suma del cuadrado de los residuos para hacer que la función de pérdida sea independiente del número de puntos de datos en el conjunto de entrenamiento.
- MSE es sensible a los valores atípicos .
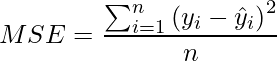
Python3
import numpy as np # Mean Squared Error def mse( y, y_pred ) : return np.sum( ( y - y_pred ) ** 2 ) / np.size( y )
where, i - ith training sample in a dataset n - number of training samples y(i) - Actual output of ith training sample y-hat(i) - Predicted value of ith training sample
Error absoluto medio (MAE) / Pérdida de La
- Es la Media de Absoluto de Residuales para todos los puntos de datos en el conjunto de datos. Los residuos son la diferencia entre la predicción real y la predicha por el modelo.
- El absoluto de residuos se realiza para convertir valores negativos en valores positivos.
- Se toma la media para hacer que la función de pérdida sea independiente del número de puntos de datos en el conjunto de entrenamiento.
- Una ventaja de MAE es que es resistente a los valores atípicos.
- Generalmente, MAE es menos preferido que MSE, ya que es más difícil calcular la derivada de la función absoluta porque la función absoluta no es diferenciable en los mínimos.

Fuente: Wikipedia
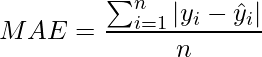
Python3
# Mean Absolute Error def mae( y, y_pred ) : return np.sum( np.abs( y - y_pred ) ) / np.size( y )
Error de sesgo medio: es lo mismo que MSE . pero menos preciso y puede concluir si el modelo tiene un sesgo positivo o un sesgo negativo.
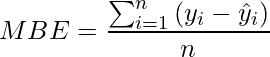
Python3
# Mean Bias Error def mbe( y, y_pred ) : return np.sum( y - y_pred ) / np.size( y )
Pérdida de Huber / Error absoluto medio suave
- Es la combinación de MSE y MAE. Toma las buenas propiedades de ambas funciones de pérdida al ser menos sensible a los valores atípicos y diferenciable en los mínimos.
- Cuando el error es menor, se utiliza la parte MSE de Huber y cuando el error es grande, se utiliza la parte MAE de Huber.
- Un nuevo hiperparámetro ‘ ???? ‘ se introduce que le dice a la función de pérdida dónde cambiar de MSE a MAE.
- ‘????’ adicional Se introducen términos en la función de pérdida para suavizar la transición de MSE a MAE.

Fuente: www.evergreeninnovations.co
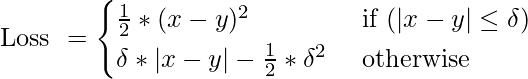
Python3
def Huber(y, y_pred, delta): condition = np.abs(y - y_pred) < delta l = np.where(condition, 0.5 * (y - y_pred) ** 2, delta * (np.abs(y - y_pred) - 0.5 * delta)) return np.sum(l) / np.size(y)
PÉRDIDAS DE CLASIFICACIÓN
Pérdida de entropía cruzada: también conocida como probabilidad logarítmica negativa . Es la función de pérdida comúnmente utilizada para la clasificación. Progreso de pérdida de entropía cruzada a medida que la probabilidad predicha diverge de la etiqueta real.
Python3
# Binary Loss def cross_entropy(y, y_pred): return - np.sum(y * np.log(y_pred) + (1 - y) * np.log(1 - y_pred)) / np.size(y)
![]()
Pérdida de bisagra : también conocida como pérdida de SVM multiclase . La pérdida de bisagra se aplica para la clasificación de margen máximo, de manera destacada para las máquinas de vectores de soporte. Es una función convexa utilizada en el optimizador convexo.
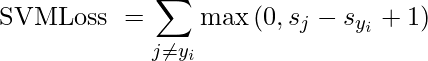
Python3
# Hinge Loss def hinge(y, y_pred): l = 0 size = np.size(y) for i in range(size): l = l + max(0, 1 - y[i] * y_pred[i]) return l / size
Publicación traducida automáticamente
Artículo escrito por lakshmiprabha y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA