Curva B-Spline en gráficos por computadora

Requisito previo: curva de Bezier

El concepto de curva B-spline vino a resolver las desventajas que tenía la curva de Bezier, ya que todos sabemos que ambas curvas son de naturaleza paramétrica. En la curva de Bezier nos enfrentamos a un problema, cuando cambiamos la ubicación respectiva del punto de control, la forma de la curva completa cambia. Pero aquí en la curva B-spline, solo un segmento específico de la forma de la curva cambia o se ve afectado por el cambio de la ubicación correspondiente de los puntos de control.

En la curva B-spline , los puntos de control imparten un control local sobre la forma de la curva en lugar del control global como la curva de Bezier.

Forma de la curva B-spline antes de cambiar la posición del punto de control P ₁ –

Forma de la curva B-spline después de cambiar la posición del punto de control P ₁ –

Puede ver en la figura anterior que solo la forma del segmento 1 , ya que solo hemos cambiado el punto de control P ₁ , y la forma del segmento 2 permanece intacta.

Curva B-spline:
Como vemos arriba, las curvas B-splines son independientes del número de puntos de control y están formadas por la unión de varios segmentos sin problemas, donde la forma de cada segmento se decide por algunos puntos de control específicos que vienen en esa región de segmento. Considere una curva dada a continuación:

Los atributos de esta curva son:

Tenemos puntos de control «n+1» en lo anterior, entonces, n+1=8, entonces n=7.
Supongamos que el orden de esta curva es ‘k’, por lo que la curva que obtendremos será de grado polinomial “k-1”. Convencionalmente se dice que el valor de ‘k’ debe estar en el rango: 2 ≤ k ≤ n+1. Entonces, supongamos que k=4, por lo que el grado de la curva será k-1 = 3.
El número total de segmentos para esta curva se calculará a través de la siguiente fórmula –
Número total. de seg = n – k + 2 = 7 – 4 + 2 = 5.

Segmentos	Puntos de control	Parámetro
S ₀	P ₀ , P ₁ , P ₂ , P ₃	0≤t≤2
S ₁	P ₁ , P ₂ , P ₃ , P ₄	2≤t≤3
S ₂	P ₂ , P ₃ , P ₄ , P ₅	3≤t≤4
S ₃	P ₃ , P ₄ , P ₅ , P ₆	4≤t≤5
S ₄	P ₄ , P ₅ , P ₆ , P ₇	5≤t≤6

Nudos en la curva B-spline:
el punto entre dos segmentos de una curva que se une entre sí, dichos puntos se conocen como nudos en la curva B-spline. En el caso de la curva de grado polinómico cúbico, los nudos son “n+4”. Pero en otros casos comunes, tenemos nudos “n+k+1” . Entonces, para la curva anterior, los vectores de nudos totales serán:

Total knots = n+k+1 = 7 + 4 + 1 = 12

Estos vectores de nudos pueden ser de tres tipos:

Uniforme (periódico)
Uniforme Abierto
no uniforme

Ecuación de la curva B-spline: La ecuación de la curva spline es la siguiente:

$\mathbf{Q(t)=\sum^n_{i=o} P_i* N_{i,k}(t)}\\ \textbf{Where \,}\mathbf{N_{i,k}}\textbf{ \,is Basis function of B-splne curve.}$

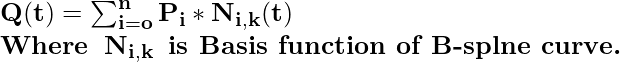
Donde P _i , k, t representa correspondientemente los puntos de control, grado, parámetro de la curva.

$\mathbf{N_{i,k}(t)=\frac{(t-x_i)*N_{i,k-1}(t)}{x_{i+k-1}-1}+\frac{(x_{i+k}-t)*N_{i+1,k-1}(t)}{x_{i+k}-x_{i+1}}}$

Y las siguientes son algunas condiciones para x _i son las siguientes:

$\mathbf{x_i=0; if\,\,i\lt k;}\\ \mathbf{x_i=i-k+1; if\,\,k\le i\le n;}\\ \mathbf{x_i=0; if\,\,i\gt n.}$

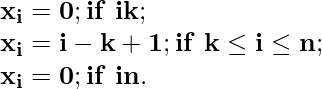
Algunos casos de función base:

$\mathbf{N_{i,k}(t)=\binom{1;\,\,if\,\,x_i\le t\le x_{i+1}}{0;\,else}}\\ \textbf{where\,}\mathbf{\,t_{min}\le t \le t_{max.}}$

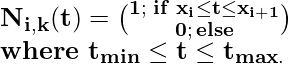
Propiedades de la curva B-spline:

Cada función base tiene un valor de 0 o +ve para todos los parámetros.
Cada función base tiene un valor máximo excepto k=1.
El grado del polinomio de la curva B-spline no depende del número de puntos de control, lo que lo hace más confiable de usar que la curva de Bezier.
La curva B-spline proporciona el control local a través de puntos de control sobre cada segmento de la curva.
La suma de funciones base para un parámetro dado es uno.

Publicación traducida automáticamente

Artículo escrito por madhav_mohan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta