¿Qué es una curva de Bézier?
Entonces, una curva de Bezier es una curva definida matemáticamente que se usa en aplicaciones gráficas bidimensionales como Adobe Illustrator, Inkscape, etc. La curva se define por cuatro puntos: la posición inicial y la posición final, es decir , P0 y P3 respectivamente (que se denominan «anclas» ) y dos puntos medios separados, es decir , P1 y P2 (que se denominan «mangos») en nuestro ejemplo. Las curvas de Bezier se utilizan con frecuencia en gráficos por computadora, animación, modelado, etc.
¿Cómo representamos matemáticamente las curvas de Bezier?
Las curvas de Bézier se pueden generar bajo el control de otros puntos. Las tangentes aproximadas mediante el uso de puntos de control se utilizan para generar la curva. La curva de Bezier se puede representar matemáticamente como – ![]()
Donde ![]() está el conjunto de puntos y
está el conjunto de puntos y ![]() representa los polinomios de Bernstein, es decir, la función de combinación que viene dada por –
representa los polinomios de Bernstein, es decir, la función de combinación que viene dada por – ![]()
Donde n es el orden del polinomio, i es el índice y u/t es la variable que tiene de 0 a 1 _
Definamos matemáticamente nuestra curva de bezier cúbica.
Entonces, una identificación de curva Bezier definida por un conjunto de puntos de control ![]() para
para ![]() donde n se llama su orden (n = 1 para lineal, n = 2 para cuadrático, etc.). Los puntos de control primero y último son siempre los puntos finales de la curva; sin embargo, los puntos de control intermedios (si los hay) generalmente no se encuentran en la curva.
donde n se llama su orden (n = 1 para lineal, n = 2 para cuadrático, etc.). Los puntos de control primero y último son siempre los puntos finales de la curva; sin embargo, los puntos de control intermedios (si los hay) generalmente no se encuentran en la curva.
Para la curva de Bézier cúbica, el orden (n) del polinomio es 3 , el índice (i) varía de i = 0 a i = n, es decir, 3 y u variará de ![]() .
.
Cubic Bezier Curve function is defined as :
![]()
Cubic Bezier Curve blending function are defined as :
![]()
![]()
![]()
![]()
So ![]()
and ![]()
Now,![]()
![]()
So we will calculate curve x and y pixel by incrementing value of u by 0.0001.
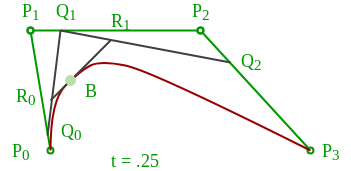
Construcción de una curva de Bézier cúbica
Properties of bezier curves
1. Siempre pasan por el primer y último control.
2. Están contenidos en el casco convexo de sus puntos de control de definición.
3. El grado del polinomio que define el segmento de la curva es uno menos que el número de puntos del polígono que lo definen. Por tanto, para 4 puntos de control, el grado del polinomio es 3, es decir, polinomio cúbico.
4. Una curva de Bézier generalmente sigue la forma del polígono que la define
. 5. La dirección del vector tangente en los extremos es la misma que la del vector determinado por el primer y el último segmento.
6. Las curvas de Bézier exhiben un control global, lo que significa que mover un punto de control altera la forma de toda la curva
NOTA: La siguiente implementación utiliza la biblioteca SDL para dibujar píxeles en la pantalla. Si está en un sistema Debian como ubuntu, simplemente ejecute el siguiente comando para instalar la biblioteca SDL.
Ej: Tenemos cuatro puntos de control B 0 [1,0], B 1 [2,2], B 2 [6,3], B 3 [8,2], así que determine los cinco puntos que se encuentran en el curve también dibuje la curva en el gráfico.
Respuesta: La curva dada tiene cuatro puntos de control, por lo tanto, es una curva de Bézier cúbica. Entonces, la ecuación paramétrica de la curva de Bézier cúbica es
![Rendered by QuickLaTeX.com \hspace{1.2cm}\mathbf{P(t)=B_0(1-t)^3+3*B_1*(1-t)^2*t+3*B_2*(1-t)*t^2+B_3*t^3} \\\\\hspace{5.8cm}\textbf{Where t is 0$\leq$t$\leq$1}\\\\ \\\\\hspace{2.8cm}\textbf{Where }\mathbf{[B_x\,\,B_y]}\textbf{ is representing scalar x \& y coordinates}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e86d666ab20bf9f6096ed6028af3f188_l3.png)
ahora, sustituya los puntos de control en la ecuación anterior para obtener,
![]()
Supongamos que cinco valores diferentes de t son {0, 0.2, 0.5, 0.7, 1}.
Entonces, para t=0 la coordenada será,
![Rendered by QuickLaTeX.com \hspace{0cm}\mathbf{P(0)=[1\,\,0]*(1-0)^3+3*[2\,\,2]*(1-0)^2*0+3*[6\,\,2]*(1-0)*0^2+[8\,\,2]*0^3}\\ \hspace{0cm}\mathbf{P(0)=[1\,\,0]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-86afa3c1fa477f284ffa48181989a024_l3.png)
Entonces, para t=0.2 la coordenada será,
![Rendered by QuickLaTeX.com \hspace{0cm}\mathbf{P(0.2)=[1\,\,0]*(1-0.2)^3+3*[2\,\,2]*(1-0.2)^2*0.2+3*[6\,\,2]*(1-0.2)*0.2^2+[8\,\,2]*0.2^3}\\ \\ \hspace{1.16cm}\mathbf{=[1\,\,0]*0.576+[2\,\,2]*0.384+[6\,\,2]*0.032+[8\,\,2]*0.2^3}\\ \hspace{1.16cm}\mathbf{=[0.576\,\,0]+[0.768\,\,0.768]+[0.192\,\,0.064]+[0.064\,\,0.016]}\\ \\ \hspace{0cm}\mathbf{P(0.2)=[1.48424\,\,\,0.848]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-418fad449e3e259012de4a266141d76b_l3.png)
Entonces, para t=0.5 la coordenada será,
![Rendered by QuickLaTeX.com \\\hspace{0cm}\mathbf{P(0.5)=[1\,\,0]*(1-0.5)^3+3*[2\,\,2]*(1-0.5)^2*0.5+3*[6\,\,2]*(1-0.5)*0.5^2+[8\,\,2]*0.5^3}\\ \\\hspace{0cm}\mathbf{P(0.5)=[4.125\,\,1.75]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2a3431529d5a38d99a23d312eb183662_l3.png)
Entonces, para t=0.7 la coordenada será,
![Rendered by QuickLaTeX.com \hspace{0cm}\mathbf{P(0.7)=[1\,\,0]*(1-0.7)^3+3*[2\,\,2]*(1-0.7)^2*0.7+3*[6\,\,2]*(1-0.7)*0.7^2+[8\,\,2]*0.7^3}\\ \\\hspace{0cm}\mathbf{P(0.7)=[5.417\,\,\,2.108]}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-59a3c70d84790f170a1f832467aea174_l3.png)
Entonces, para t=1.0 la coordenada será,
![Rendered by QuickLaTeX.com \\\hspace{0cm}\mathbf{P(1.0)=[1\,\,0]*(1-1)^3+3*[2\,\,2]*(1-1)^2*1+3*[6\,\,2]*(1-1)*1^2+[8\,\,2]*1^3}\\ \hspace{0cm}\mathbf{P(1.0)=[8\,\,\,2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d884b82ef7da2eae64cf361870a350b6_l3.png)

Figura 1
a) El grado de la curva de Bezier depende del número de puntos de control asociados con la curva correspondiente, a medida que aumenta el número de puntos de control, el grado del polinomio de la ecuación de la curva también aumenta, lo que hace que la ecuación de la curva sea muy compleja y más difícil de manejar.
Degree of curve = no. of control points - 1
b) Una de las principales desventajas de usar la curva de Bezier es que imparten un control global a la curva. Lo que significa que si la posición relativa de la curva cambia, la forma de toda la curva cambia. Esto hace que sea menos conveniente de usar.

Al cambiar la posición relativa de cualquiera de los puntos de control, toda la forma de la curva cambia:

c) Un problema más con Bezier es que su función de mezcla nunca llega a cero para ningún parámetro, independientemente del grado de la curva.
sudo apt-get install libsdl2-dev
Para construir uso
gcc fileName.c -lSDL2 -lm
C
// C program to implement
// Cubic Bezier Curve
/* install SDL library for running thing code*/
/* install by using this commamnd line : sudo apt-get install libsdl2-dev */
/* run this code using command : gcc fileName.c -lSDL2 -lm*/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<SDL2/SDL.h>
SDL_Window* window = NULL;
SDL_Renderer* renderer = NULL;
int mousePosX , mousePosY ;
int xnew , ynew ;
/*Function to draw all other 7 pixels present at symmetric position*/
void drawCircle(int xc, int yc, int x, int y)
{
SDL_RenderDrawPoint(renderer,xc+x,yc+y) ;
SDL_RenderDrawPoint(renderer,xc-x,yc+y);
SDL_RenderDrawPoint(renderer,xc+x,yc-y);
SDL_RenderDrawPoint(renderer,xc-x,yc-y);
SDL_RenderDrawPoint(renderer,xc+y,yc+x);
SDL_RenderDrawPoint(renderer,xc-y,yc+x);
SDL_RenderDrawPoint(renderer,xc+y,yc-x);
SDL_RenderDrawPoint(renderer,xc-y,yc-x);
}
/*Function for circle-generation using Bresenham's algorithm */
void circleBres(int xc, int yc, int r)
{
int x = 0, y = r;
int d = 3 - 2 * r;
while (y >= x)
{
/*for each pixel we will draw all eight pixels */
drawCircle(xc, yc, x, y);
x++;
/*check for decision parameter and correspondingly update d, x, y*/
if (d > 0)
{
y--;
d = d + 4 * (x - y) + 10;
}
else
d = d + 4 * x + 6;
drawCircle(xc, yc, x, y);
}
}
/* Function that take input as Control Point x_coordinates and
Control Point y_coordinates and draw bezier curve */
void bezierCurve(int x[] , int y[])
{
double xu = 0.0 , yu = 0.0 , u = 0.0 ;
int i = 0 ;
for(u = 0.0 ; u <= 1.0 ; u += 0.0001)
{
xu = pow(1-u,3)*x[0]+3*u*pow(1-u,2)*x[1]+3*pow(u,2)*(1-u)*x[2]
+pow(u,3)*x[3];
yu = pow(1-u,3)*y[0]+3*u*pow(1-u,2)*y[1]+3*pow(u,2)*(1-u)*y[2]
+pow(u,3)*y[3];
SDL_RenderDrawPoint(renderer , (int)xu , (int)yu) ;
}
}
int main(int argc, char* argv[])
{
/*initialize sdl*/
if (SDL_Init(SDL_INIT_EVERYTHING) == 0)
{
/*
This function is used to create a window and default renderer.
int SDL_CreateWindowAndRenderer(int width
,int height
,Uint32 window_flags
,SDL_Window** window
,SDL_Renderer** renderer)
return 0 on success and -1 on error
*/
if(SDL_CreateWindowAndRenderer(640, 480, 0, &window, &renderer) == 0)
{
SDL_bool done = SDL_FALSE;
int i = 0 ;
int x[4] , y[4] , flagDrawn = 0 ;
while (!done)
{
SDL_Event event;
/*set background color to black*/
SDL_SetRenderDrawColor(renderer, 0, 0, 0, SDL_ALPHA_OPAQUE);
SDL_RenderClear(renderer);
/*set draw color to white*/
SDL_SetRenderDrawColor(renderer, 255, 255, 255, SDL_ALPHA_OPAQUE);
/* We are drawing cubic bezier curve
which has four control points */
if(i==4)
{
bezierCurve(x , y) ;
flagDrawn = 1 ;
}
/*grey color circle to encircle control Point P0*/
SDL_SetRenderDrawColor(renderer, 128, 128, 128, SDL_ALPHA_OPAQUE);
circleBres(x[0] , y[0] , 8) ;
/*Red Line between control Point P0 & P1*/
SDL_SetRenderDrawColor(renderer, 255, 0, 0, SDL_ALPHA_OPAQUE);
SDL_RenderDrawLine(renderer , x[0] , y[0] , x[1] , y[1]) ;
/*grey color circle to encircle control Point P1*/
SDL_SetRenderDrawColor(renderer, 128, 128, 128, SDL_ALPHA_OPAQUE);
circleBres(x[1] , y[1] , 8) ;
/*Red Line between control Point P1 & P2*/
SDL_SetRenderDrawColor(renderer, 255, 0, 0, SDL_ALPHA_OPAQUE);
SDL_RenderDrawLine(renderer , x[1] , y[1] , x[2] , y[2]) ;
/*grey color circle to encircle control Point P2*/
SDL_SetRenderDrawColor(renderer, 128, 128, 128, SDL_ALPHA_OPAQUE);
circleBres(x[2] , y[2] , 8) ;
/*Red Line between control Point P2 & P3*/
SDL_SetRenderDrawColor(renderer, 255, 0, 0, SDL_ALPHA_OPAQUE);
SDL_RenderDrawLine(renderer , x[2] , y[2] , x[3] , y[3]) ;
/*grey color circle to encircle control Point P3*/
SDL_SetRenderDrawColor(renderer, 128, 128, 128, SDL_ALPHA_OPAQUE);
circleBres(x[3] , y[3] , 8) ;
/*We are Polling SDL events*/
if (SDL_PollEvent(&event))
{
/* if window cross button clicked then quit from window */
if (event.type == SDL_QUIT)
{
done = SDL_TRUE;
}
/*Mouse Button is Down */
if(event.type == SDL_MOUSEBUTTONDOWN)
{
/*If left mouse button down then store
that point as control point*/
if(event.button.button == SDL_BUTTON_LEFT)
{
/*store only four points
because of cubic bezier curve*/
if(i < 4)
{
printf("Control Point(P%d):(%d,%d)\n"
,i,mousePosX,mousePosY) ;
/*Storing Mouse x and y positions
in our x and y coordinate array */
x[i] = mousePosX ;
y[i] = mousePosY ;
i++ ;
}
}
}
/*Mouse is in motion*/
if(event.type == SDL_MOUSEMOTION)
{
/*get x and y positions from motion of mouse*/
xnew = event.motion.x ;
ynew = event.motion.y ;
int j ;
/* change coordinates of control point
after bezier curve has been drawn */
if(flagDrawn == 1)
{
for(j = 0 ; j < i ; j++)
{
/*Check mouse position if in b/w circle then
change position of that control point to mouse new
position which are coming from mouse motion*/
if((float)sqrt(abs(xnew-x[j]) * abs(xnew-x[j])
+ abs(ynew-y[j]) * abs(ynew-y[j])) < 8.0)
{
/*change coordinate of jth control point*/
x[j] = xnew ;
y[j] = ynew ;
printf("Changed Control Point(P%d):(%d,%d)\n"
,j,xnew,ynew) ;
}
}
}
/*updating mouse positions to positions
coming from motion*/
mousePosX = xnew ;
mousePosY = ynew ;
}
}
/*show the window*/
SDL_RenderPresent(renderer);
}
}
/*Destroy the renderer and window*/
if (renderer)
{
SDL_DestroyRenderer(renderer);
}
if (window)
{
SDL_DestroyWindow(window);
}
}
/*clean up SDL*/
SDL_Quit();
return 0;
}
Output
Mueva el mouse cuando la posición del mouse sea un círculo en blanco y negro, luego solo se cambiará la forma de la curva



Referencias:
https://en.wikipedia.org/wiki/B%C3%A9zier_curve
https://www.tutorialspoint.com/computer_graphics/computer_graphics_curves.htm
http://www.math.ucla.edu/~baker/149.1 .02w/handouts/bb_bezier.pdf
Este artículo es una contribución de Palkansh Khandelwal
Publicación traducida automáticamente
Artículo escrito por Palkansh Khandelwal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA