Óptimo local y global en optimización univariante

La optimización univariada es un caso simple de un problema de optimización no lineal con un caso sin restricciones, es decir, no hay ninguna restricción. La optimización univariante se puede definir como una optimización no lineal sin restricciones y solo hay una variable de decisión en esta optimización para la que estamos tratando de encontrar un valor.

min f(x) tal que x ∈ R

donde,
f(x) = Función objetivo
x = Variable de decisión

Entonces, cuando miras este problema de optimización, normalmente lo escribes en la forma anterior donde dices que vas a minimizar f(x) , y esta función se llama función objetivo. Y la variable que puede usar para minimizar esta función, que se llama la variable de decisión, se escribe a continuación así: wrt x aquí y también dice que x es continua, es decir, podría tomar cualquier valor en la línea de números reales. Y dado que este es un problema de optimización univariado, x es una variable escalar y no una variable vectorial.

Función convexa:

Siempre que hablamos de problemas de optimización univariante, es fácil visualizarlo en una imagen 2D como esta.

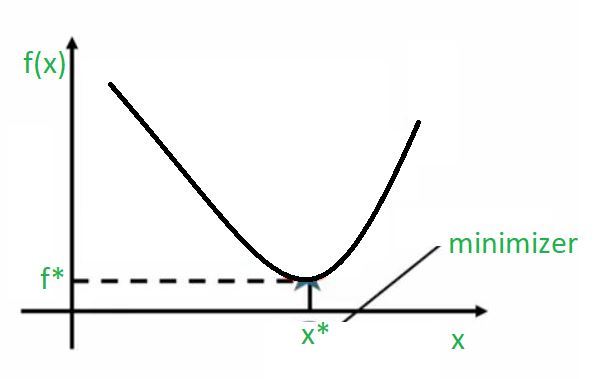
Entonces, lo que tenemos aquí está en el eje x, tenemos diferentes valores para la variable de decisión x y en el eje y, tenemos el valor de la función. Y cuando trazas esto, puedes notar fácilmente en el gráfico que marcó el punto en el que esta función alcanza su valor mínimo. Entonces, el punto en el que esta función alcanza el valor mínimo se puede encontrar colocando una perpendicular sobre el eje x. Entonces, puede decir que x* es el valor real de x en el que esta función toma un valor mínimo y el valor que toma la función en su punto mínimo se puede identificar colocando esta perpendicular en el eje y y esta f* es la el mejor valor que esta función podría tomar. Entonces, las funciones de este tipo se llaman funciones convexasporque solo hay un mínimo aquí. Por lo tanto, no se trata de múltiples mínimos para elegir, solo hay un mínimo aquí, y eso está marcado en el gráfico. Entonces, en este caso, diríamos que este mínimo es tanto un mínimo local como un mínimo global . De hecho, podemos decir que es un mínimo local porque en las proximidades de este punto es la mejor solución que se puede conseguir. Y si la solución que obtenemos en la vecindad de este punto es también la mejor solución a nivel mundial, entonces también lo llamamos el mínimo global .

Función no convexa:

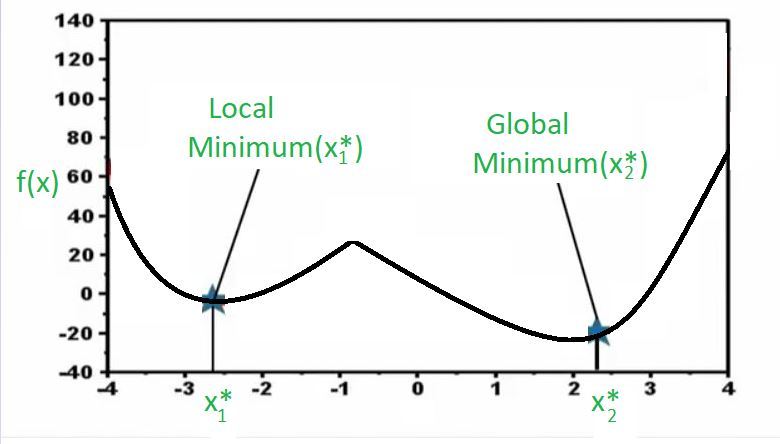
Ahora, eche un vistazo al gráfico anterior. Aquí tengo una función y nuevamente es un problema de optimización univariante. Entonces, en el eje x, tengo diferentes valores de la variable de decisión y en el eje y , graficamos la función. Ahora, puede notar que hay dos puntos donde la función alcanza un mínimo y puede ver que cuando decimos mínimo automáticamente en realidad solo queremos decir localmente mínimo porque si nota este punto x1* en el gráfico, en la vecindad de este punto , esta función no puede tomar ningún valor mejor desde el punto de vista de la minimización. En otras palabras, si estoy en x1*y la función está tomando este valor, si me muevo hacia la derecha, el valor de la función aumentará, lo que básicamente no es bueno para nosotros porque estamos tratando de encontrar el valor mínimo, y si me muevo hacia la izquierda, el valor de la función aumentará nuevamente, lo cual no es bueno porque estamos encontrando el mínimo para esta función. Lo que esto básicamente dice es lo siguiente.

Esto dice que en una vecindad local nunca puedes encontrar un punto que sea mejor que este. Sin embargo, si se aleja, llegará a este punto (x2*) aquí, que de nuevo desde un punto de vista local es el mejor porque si vamos en la dirección correcta la función aumenta y si vamos en la dirección izquierda también la función aumenta, y en este ejemplo particular también resulta que globalmente esta es la mejor solución. Entonces, si bien ambos son mínimos locales en el sentido de que en la vecindad son los mejores, este mínimo local (x2*) también es un mínimo global porque si tomas toda la región aún no puedes superar esta solución. Entonces, cuando tiene una solución que es la más baja en toda la región, la llamamos mínimo global. Y estos son tipos de funciones que llamamos comofunciones no convexas donde hay múltiples óptimos locales y el trabajo de un optimizador es encontrar la mejor solución de las muchas soluciones óptimas que son posibles.

¿Por qué este concepto es importante para la ciencia de datos?

Hagamos una conexión entre este concepto y la ciencia de datos. Este problema de encontrar el mínimo global ha sido un problema real en varios algoritmos de ciencia de datos. Por ejemplo, en los años 90 hubo mucho entusiasmo e interés en las redes neuronales, etc., y durante algunos años se investigó mucho sobre las redes neuronales y, en muchos casos, resultó que encontrar la solución óptima global era muy difícil. y, en muchos casos, estas redes neuronales se entrenaron con óptimos locales que no son lo suficientemente buenos para el tipo de problemas que se estaban resolviendo. Entonces, eso se convirtió en un problema real con la noción de redes neuronales, y luego, en los últimos años, este problema ha sido revisado y ahora hay algoritmos mucho mejores, formas funcionales mucho mejores y estrategias de entrenamiento mucho mejores.