Requisito previo: Introducción a word2vec
El procesamiento del lenguaje natural (NLP) es un subcampo de la informática y la inteligencia artificial relacionado con las interacciones entre las computadoras y los lenguajes humanos (naturales).
En las técnicas de PNL, mapeamos las palabras y frases (de vocabulario o corpus) a vectores de números para facilitar el procesamiento. Estos tipos de técnicas de modelado del lenguaje se denominan incrustaciones de palabras .
En 2013, Google anunció word2vec , un grupo de modelos relacionados que se utilizan para producir incrustaciones de palabras.
Implementemos nuestro propio modelo skip-gram (en Python) derivando las ecuaciones de retropropagación de nuestra red neuronal.
Enomita la arquitectura de gramo de word2vec, la entrada es la palabra central y las predicciones son las palabras de contexto. Considere una array de palabras W, si W(i) es la entrada (palabra central), entonces W(i-2), W(i-1), W(i+1) y W(i+2) son las palabras de contexto, si el tamaño de la ventana deslizante es 2.
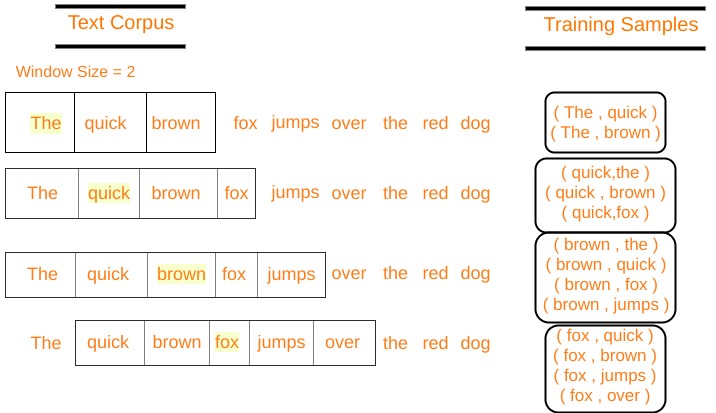
Let's define some variables : V Number of unique words in our corpus of text ( Vocabulary ) x Input layer (One hot encoding of our input word ). N Number of neurons in the hidden layer of neural network W Weights between input layer and hidden layer W' Weights between hidden layer and output layer y A softmax output layer having probabilities of every word in our vocabulary
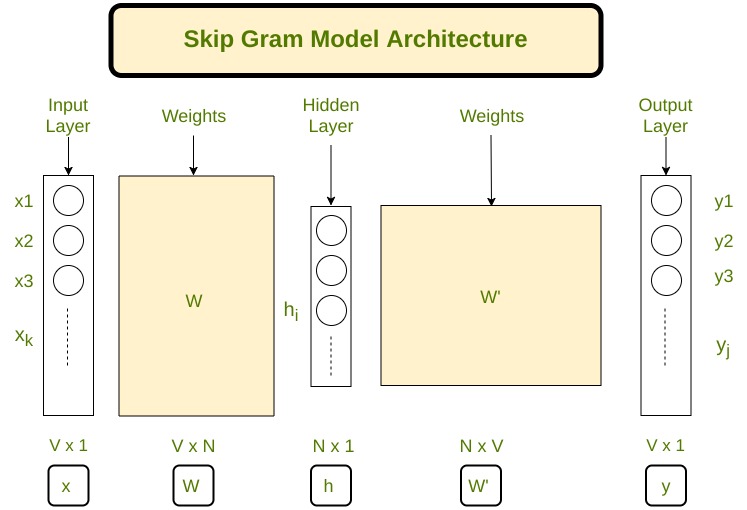
Saltar la arquitectura de gramo
Nuestra arquitectura de red neuronal está definida, ahora hagamos algunas matemáticas para derivar las ecuaciones necesarias para el descenso de gradiente.
Propagación hacia adelante:
Multiplicando una codificación en caliente de la palabra central (indicada por x ) con la primera array de peso W para obtener la array de capa oculta h (de tamaño N x 1). ![]()
( Vx1 ) ( NxV ) ( Vx1 ) Ahora multiplicamos el vector de capa oculta h con la segunda array de peso W’ para obtener una nueva array u ( Vx1 ) ( VxN ) ( Nx1 ) Tenga en cuenta que tenemos que aplicar un softmax> a la capa u para obtener nuestra capa de salida y . Sea u j la j ésima neurona de la capa u Sea w j la j ésima ![]()
palabra en nuestro vocabulario donde j es cualquier índice
Sea V wj la j -ésima columna de la array W’ (columna correspondiente a una palabra w j ) ![]()
( 1×1 ) ( 1xN ) ( Nx1 ) y = softmax(u) y j = softmax(u j ) y j denota la probabilidad de que w j sea una palabra de contexto P(w j |w i ) es la probabilidad de que w j sea una palabra de contexto, dado que w i es la palabra de entrada. Por lo tanto, nuestro objetivo es maximizar P( w j* | w
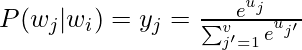
i ) , donde j* representa los índices de las palabras de contexto
Claramente queremos maximizar 
donde j* c son los índices de vocabulario de las palabras de contexto. Las palabras de contexto van desde c = 1, 2, 3..C.
Tomemos una probabilidad logarítmica negativa de esta función para obtener nuestra función de pérdida , que queremos minimizar 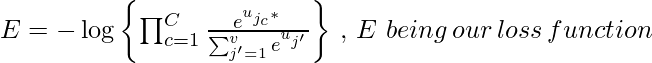
. Sea t el vector de salida real de nuestros datos de entrenamiento, para una palabra central en particular. . Tendrá 1 en las posiciones de las palabras de contexto y 0 en todos los demás lugares. t j*c son los 1 de las palabras de contexto.
Podemos multiplicar ![]() con
con ![]()
![]()
Resolviendo esta ecuación obtenemos nuestra función de pérdida como – ![]()
Propagación hacia atrás:
Los parámetros a ajustar están en las arrays W y W’, por lo que debemos encontrar las derivadas parciales de nuestra función de pérdida con respecto a W y W’ para aplicar el algoritmo de descenso de gradiente.
Tenemos que encontrar ![]()
![]()
![]()
![]()
![]()

![]()
Now, Finding ![]()
![]()
![]()
![]()
![]()
Below es la implementación:
Python3
import numpy as np
import string
from nltk.corpus import stopwords
def softmax(x):
"""Compute softmax values for each sets of scores in x."""
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum()
class word2vec(object):
def __init__(self):
self.N = 10
self.X_train = []
self.y_train = []
self.window_size = 2
self.alpha = 0.001
self.words = []
self.word_index = {}
def initialize(self,V,data):
self.V = V
self.W = np.random.uniform(-0.8, 0.8, (self.V, self.N))
self.W1 = np.random.uniform(-0.8, 0.8, (self.N, self.V))
self.words = data
for i in range(len(data)):
self.word_index[data[i]] = i
def feed_forward(self,X):
self.h = np.dot(self.W.T,X).reshape(self.N,1)
self.u = np.dot(self.W1.T,self.h)
#print(self.u)
self.y = softmax(self.u)
return self.y
def backpropagate(self,x,t):
e = self.y - np.asarray(t).reshape(self.V,1)
# e.shape is V x 1
dLdW1 = np.dot(self.h,e.T)
X = np.array(x).reshape(self.V,1)
dLdW = np.dot(X, np.dot(self.W1,e).T)
self.W1 = self.W1 - self.alpha*dLdW1
self.W = self.W - self.alpha*dLdW
def train(self,epochs):
for x in range(1,epochs):
self.loss = 0
for j in range(len(self.X_train)):
self.feed_forward(self.X_train[j])
self.backpropagate(self.X_train[j],self.y_train[j])
C = 0
for m in range(self.V):
if(self.y_train[j][m]):
self.loss += -1*self.u[m][0]
C += 1
self.loss += C*np.log(np.sum(np.exp(self.u)))
print("epoch ",x, " loss = ",self.loss)
self.alpha *= 1/( (1+self.alpha*x) )
def predict(self,word,number_of_predictions):
if word in self.words:
index = self.word_index[word]
X = [0 for i in range(self.V)]
X[index] = 1
prediction = self.feed_forward(X)
output = {}
for i in range(self.V):
output[prediction[i][0]] = i
top_context_words = []
for k in sorted(output,reverse=True):
top_context_words.append(self.words[output[k]])
if(len(top_context_words)>=number_of_predictions):
break
return top_context_words
else:
print("Word not found in dictionary")
Python3
def preprocessing(corpus):
stop_words = set(stopwords.words('english'))
training_data = []
sentences = corpus.split(".")
for i in range(len(sentences)):
sentences[i] = sentences[i].strip()
sentence = sentences[i].split()
x = [word.strip(string.punctuation) for word in sentence
if word not in stop_words]
x = [word.lower() for word in x]
training_data.append(x)
return training_data
def prepare_data_for_training(sentences,w2v):
data = {}
for sentence in sentences:
for word in sentence:
if word not in data:
data[word] = 1
else:
data[word] += 1
V = len(data)
data = sorted(list(data.keys()))
vocab = {}
for i in range(len(data)):
vocab[data[i]] = i
#for i in range(len(words)):
for sentence in sentences:
for i in range(len(sentence)):
center_word = [0 for x in range(V)]
center_word[vocab[sentence[i]]] = 1
context = [0 for x in range(V)]
for j in range(i-w2v.window_size,i+w2v.window_size):
if i!=j and j>=0 and j<len(sentence):
context[vocab[sentence[j]]] += 1
w2v.X_train.append(center_word)
w2v.y_train.append(context)
w2v.initialize(V,data)
return w2v.X_train,w2v.y_train
Python3
corpus = ""
corpus += "The earth revolves around the sun. The moon revolves around the earth"
epochs = 1000
training_data = preprocessing(corpus)
w2v = word2vec()
prepare_data_for_training(training_data,w2v)
w2v.train(epochs)
print(w2v.predict("around",3))
Producción:

Publicación traducida automáticamente
Artículo escrito por mayank2498 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA