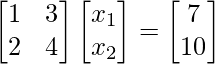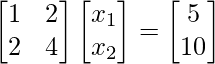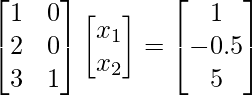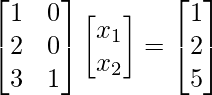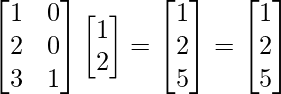Ciencia de datos | Resolviendo Ecuaciones Lineales

Puede leer el artículo Introducción a la ciencia de datos: Habilidades requeridas para tener una comprensión básica de lo que es la ciencia de datos .
El álgebra lineal es una parte muy fundamental de la ciencia de datos. Cuando se habla de ciencia de datos, la representación de datos se convierte en un aspecto importante de la ciencia de datos. Los datos se representan generalmente en forma de array. La segunda cosa importante en la perspectiva de Data Science es que si estos datos contienen varias variables de interés, entonces uno está interesado en saber cuántas de estas son muy importantes. Y si hay relaciones entre estas variables, entonces, ¿cómo se pueden descubrir estas relaciones? Las herramientas algebraicas lineales nos permiten comprender estos datos. Por lo tanto, un entusiasta de la ciencia de datos debe tener una buena comprensión de este concepto antes de comprender los complejos algoritmos de aprendizaje automático.
Arrays y Álgebra Lineal
Hay muchas formas de representar los datos, las arrays le brindan una forma conveniente de organizar estos datos.

Las arrays se pueden usar para representar muestras con múltiples atributos en una forma compacta
Las arrays también se pueden utilizar para representar ecuaciones lineales de forma compacta y sencilla.
El álgebra lineal proporciona herramientas para comprender y manipular arrays para obtener conocimiento útil de los datos.

Identificación de relaciones lineales entre atributos
Identificamos la relación lineal entre atributos utilizando el concepto de espacio nulo y nulidad. Antes de continuar, vaya a Null Space y Nullity of a Matrix .
Preliminares

Generalized linear equations are represented as below:
[Tex]A (m * n); x (n * 1); b (m * 1)[/Tex]m and n are the number of equations and variables respectivelyb is the general RHS commonly used

En general, hay tres casos que uno necesita entender:

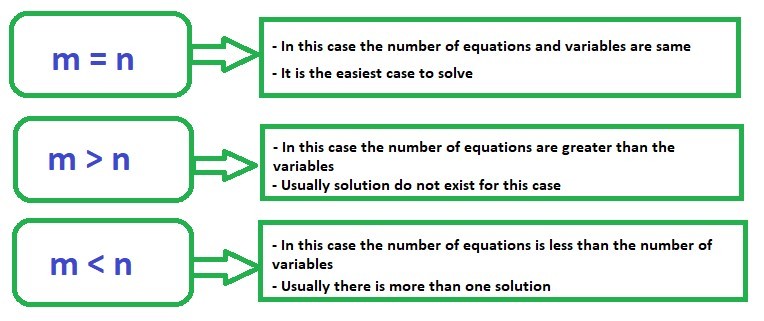
Consideraremos estos tres casos de forma independiente.
Rango de fila completa y rango de columna completa
Para una array A (mxn)

Rango de fila completa	Clasificación de columna completa
Cuando todas las filas de la array son linealmente independientes	Cuando todas las columnas de la array son linealmente independientes
El muestreo de datos no presenta una relación lineal – las muestras son independientes	Los atributos son linealmente independientes

Nota: En general, cualquiera que sea el tamaño de la array, se establece que el rango de las filas siempre es igual al rango de las columnas. Significa que para cualquier tamaño de la array si tenemos cierto número de filas independientes, tendremos esos muchos números de columnas independientes.
En general, si tenemos una array mxn y m es menor que n , entonces el rango máximo de la array solo puede ser m . Entonces, el rango máximo es siempre el menor de los dos números m y n .
Caso 1: m = n

Ejemplo 1.1:

Consider the given matrix equation:
|A| is not equal to zerorank(A) = 2 = no. of columnsThis implies that A is full rankTherefore, the solution for the given example is

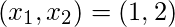
Programa para encontrar el rango y la inversa de una array y resolver la ecuación de la array en Python:

Python3

# First, import
# matrix_rank from numpy.linalg
from numpy.linalg import matrix_rank, inv, solve
 
# A 2 x 2 matrix
A = [[1, 3], 
     [2, 4]]
b = [7, 10]
  
# Rank of matrix A
print("Rank of the matrix is:", matrix_rank(A))
  
# Inverse of matrix A
print("\nInverse of A:\n", inv(A))
  
# Matrix equation solution
print("Solution of linear equations:", solve(A, b))

Producción:

Rank of the matrix is: 2

Inverse of A:
 [[-2.   1.5]
 [ 1.  -0.5]]

Solution of linear equation: [ 1.  2.]

Puede consultar Numpy | Artículo de Álgebra Lineal para varias operaciones en arrays y para resolver ecuaciones lineales en Python.
Ejemplo 1.2:

Consider the given matrix equation:
|A| is not equal to zerorank(A) = 1nullity = 1Checking consistencyRow (2) = 2 Row (1)The equations are consistent with only one linearly independent equationThe solution set for (, ) is infinite because we have onlyone linearly independent equation and two variables

Explicación: En el ejemplo anterior, solo tenemos una ecuación linealmente independiente, es decir, $x_1+2x_2 = 5$ . Entonces, si tomamos $x_2 = 0$ , entonces tenemos $x_1 = 5$ ; si tomamos $x_2 = 1$ , entonces tenemos $x_1 = 3$ . De manera similar, podemos tener muchas soluciones para esta ecuación. Podemos tomar cualquier valor de $x_2$ (tenemos infinitas opciones para $x_2$ ) y correspondientemente para cada valor de $x_2$ obtendremos uno $x_1$ . Por lo tanto, podemos decir que esta ecuación tiene infinitas soluciones.
Ejemplo 1.3:

Consider the given matrix equation:
|A| is not equal to zerorank(A) = 1nullity = 1Checking consistency2 Row (1) = Therefore, the equations are inconsistentWe cannot find the solution to ()

Caso 2: m > n

En este caso, el número de variables o atributos es menor que el número de ecuaciones.
Aquí, no todas las ecuaciones pueden ser satisfechas.
Por lo tanto, a veces se denomina como el caso sin solución.
Pero podemos tratar de identificar una solución adecuada al ver este caso desde la perspectiva de la optimización.

Una perspectiva de optimización

- Rather than finding a solution to , we can find an  such that ()   is minimized- Here,  is a vector- There will be as many error terms as the number of equations- Denote  = e (m x 1); there are m errors , i = 1:m- We can minimize all the errors collectively by minimizing - This is the same as minimizing

Entonces, el problema de optimización se convierte en
$min[(Ax-b)^{T}(Ax-b)]$
= $min[(b^{T}-x^{T}A^{T})(Ax-b)]$
= $min[(x^{T}A^{T}Ax2b^{T}Ax+b^{T}b)=f(x)]$
Aquí, podemos notar que el problema de optimización es una función de x . Cuando resolvamos este problema de optimización, nos dará la solución para x . Podemos obtener la solución a este problema de optimización derivando $f(x)$ con respecto ax y poniendo el diferencial a cero. $\begin{document} \nabla$f(x) = 0 \end{document}$
– Ahora, derivar f(x) y establecer el diferencial en cero da como resultado
$2(A^{T}A)x - 2A^{T}b = 0$
$A^{T}Ax = A^{T}b$
: – Asumir que todas las columnas son linealmente independientes
$x = (A^{T}A)^{-1}A^{T}b$
Nota: Si bien esta solución x podría no satisfacer toda la ecuación, garantizará que los errores en las ecuaciones se minimicen colectivamente .
Ejemplo 2.1:

Consider the given matrix equation:
m = 3, n = 2Using the optimization concept[Tex]\begin{bmatrix}
x_1\\
x_2\\
\end{bmatrix}
=
&&(\begin{bmatrix}
1&2&3\\
0&0&1\\
\end{bmatrix}
%
\begin{bmatrix}
1&0\\
2&0\\
3&1\\
\end{bmatrix})&&^{-1}
\begin{bmatrix}
1&2&3\\
0&0&1\\
\end{bmatrix}
%
\begin{bmatrix}
1\\
-0.5\\
5\\
\end{bmatrix}[/Tex][Tex]\begin{bmatrix}
x_1\\
x_2\\
\end{bmatrix}
=
\begin{bmatrix}
0\\
5\\
\end{bmatrix}[/Tex]Therefore, the solution for the given linear equation is Substituting in the equation shows

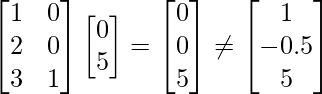
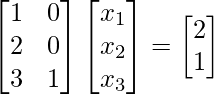
Ejemplo 2.2:

Consider the given matrix equation:
m = 3, n = 2Using the optimization concept[Tex]\begin{bmatrix}
x_1\\
x_2\\
\end{bmatrix}
=
&&(\begin{bmatrix}
1&2&3\\
0&0&1\\
\end{bmatrix}
%
\begin{bmatrix}
1&0\\
2&0\\
3&1\\
\end{bmatrix})&&^{-1}
\begin{bmatrix}
1&2&3\\
0&0&1\\
\end{bmatrix}
%
\begin{bmatrix}
1\\
2\\
5\\
\end{bmatrix}[/Tex][Tex]\begin{bmatrix}
x_1\\
x_2\\
\end{bmatrix}
=
\begin{bmatrix}
1\\
2\\
\end{bmatrix}[/Tex]Therefore, the solution for the given linear equation is Substituting in the equation shows

Entonces, el punto importante a notar en el caso 2 es que si tenemos más ecuaciones que variables, siempre podemos usar la solución de mínimos cuadrados que es $x = (A^{T}A)^{-1}A^{T}b$ . Hay una cosa a tener en cuenta es que $(A^{T}A)^{-1}$ existe si las columnas de A son linealmente independientes.
Caso 3: m < n

Este caso trata con más cantidad de atributos o variables que ecuaciones
Aquí, podemos obtener múltiples soluciones para los atributos
Este es un caso de solución infinita.
Veremos cómo podemos elegir una solución del conjunto de infinitas soluciones posibles

En este caso también tenemos una perspectiva de optimización. Conozca qué es la función de Lagrange aquí .
– A continuación se presenta el problema de optimización
min( $\frac{1}{2}x^{T}x$ )
tal que,
$Ax = b$
– Podemos definir una función lagrangiana
$min[ f(x, \lambda) = \frac{1}{2}x^{T}x + \lambda^{T}(Ax-b)]$
– Derivamos la función lagrangiana con respecto ax, y la ponemos a cero, entonces obtendremos,
$x + A^{T}\lambda = 0$
$x = -A^{T}\lambda$
Pre – multiplicando por A
$Ax=b=-AA^{T}\lambda = 0$
De arriba podemos obtener
$\lambda = -(AA^{T})^{-1}b$ suponiendo que todas las filas son linealmente independientes
$x = -A^{T}\lambda = A^{T}(AA^{T})^{-1}b$
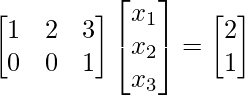
Ejemplo 3.1:

Consider the given matrix equation:
m = 2, n = 3Using the optimization concept,[Tex]x = 
\begin{bmatrix}
1&0\\
2&0\\
3&1\\
\end{bmatrix}
%
(\begin{bmatrix}
1&2&3\\
0&0&1\\
\end{bmatrix}
%
\begin{bmatrix}
1&0\\
2&0\\
3&1\\
\end{bmatrix})^{-1}
%
\begin{bmatrix}
2\\
1\\
\end{bmatrix}[/Tex][Tex]x = 
\begin{bmatrix}
1&0\\
2&0\\
3&1\\
\end{bmatrix}
%
\begin{bmatrix}
-0.2\\
1.6\\
\end{bmatrix}[/Tex]The solution for given sample is () = (-0.2, -0.4, 1)You can easily verify that

Generalización

Los casos descritos anteriormente cubren todos los escenarios posibles que uno puede encontrar al resolver ecuaciones lineales.
El concepto que usamos para generalizar las soluciones para todos los casos anteriores se llama Moore – Penrose Pseudoinverse of a matrix.
La descomposición en valores singulares se puede utilizar para calcular la pseudoinversa o la inversa generalizada ( $A^+$ ).

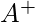Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Python3

Deja una respuesta Cancelar la respuesta