Valores de espacio propio y espectro propio en una array

Posted on by Rudeus Greyrat

requisitos previos:

Para una array A dada , el conjunto de todos los vectores propios de A asociados con un valor propio \lambdaabarca un subespacio, que se denomina espacio propio de A con respecto a \lambday se denota por E_\lambda. El conjunto de todos los valores propios de A se denomina espectro propio , o simplemente espectro, de A.
Si \lambdaes un valor propio de A, entonces el espacio propio correspondiente E_\lambdaes el espacio solución del sistema homogéneo de ecuaciones lineales(A-\lambda I)x = 0. Geométricamente, el vector propio correspondiente a un valor propio distinto de cero apunta en una dirección que se estira por el mapeo lineal. El valor propio es el factor por el cual se estira. Si el valor propio es negativo, entonces se invierte la dirección del estiramiento.

A continuación se presentan algunas propiedades útiles de valores propios y vectores propios, además de las propiedades que ya se enumeran en el artículo Matemáticas | Valores propios y vectores propios .

  • Una array A y su transpuesta A^{T}poseen los mismos valores propios pero no necesariamente los mismos vectores propios.
  • El espacio propio E_\lambdaes el espacio nulo de A - \lambda Iya que
    Ax = \lambda x \Longleftrightarrow Ax - \lambda x = 0 \Longleftrightarrow (A - \lambda I)x = 0 \Longleftrightarrow x\in ker(A - \lambda I)

    • Nota: ker significa Kernel , que es otro nombre para espacio nulo .

    Cálculo de valores propios, vectores propios y espacios propios:

    Consider given 2 X 2 matrix:
 A =  \begin{bmatrix}  4 & 2 \\ 1 & 3  \end{bmatrix} 

Step 1: Characteristic polynomial and Eigenvalues.
The characteristic polynomial is given by 
det(A - \lambda I) 

 = det(\begin{bmatrix}  4 & 2 \\ 1 & 3  \end{bmatrix} - \begin{bmatrix}  \lambda & 0 \\ 0 & \lambda  \end{bmatrix}) = \begin{vmatrix}  4-\lambda & 2 \\ 1 & 3-\lambda  \end{vmatrix} 

= (4-\lambda)(3-\lambda) - 2.1

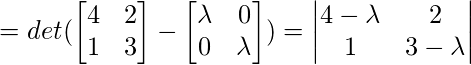
After we factorize the characteristic polynomial, we will get

(2-\lambda)(5-\lambda)

which gives eigenvalues as \lambda_1 = 2 and \lambda_2 = 5

Step 2: Eigenvectors and Eigenspaces
We find the eigenvectors that correspond to these eigenvalues by looking 
at vectors x such that 
 
  \begin{bmatrix}  4-\lambda & 2 \\ 1 & 3-\lambda  \end{bmatrix}  % x =  0  

For \lambda = 5 we obtain

  \begin{bmatrix}  4-5 & 2 \\ 1 & 3-5  \end{bmatrix} % \begin{bmatrix}  x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix}  -1 & 2 \\ 1 & -2  \end{bmatrix} % \begin{bmatrix}  x_1 \\ x_2 \end{bmatrix} = 0 

After solving the above homogeneous system of equations,
we will obtain a solution space

E_5 = span(\begin{bmatrix}  2 \\ 1 \end{bmatrix})

This eigenspace is one dimensional as it possesses a single basis vector.
Similarly, we find eigenvector for \lambda = 2 by solving
the homogeneous system of equations

  \begin{bmatrix}  4-2 & 2 \\ 1 & 3-2  \end{bmatrix} % \begin{bmatrix}  x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix}  2 & 2 \\ 1 & 1  \end{bmatrix} % \begin{bmatrix}  x_1 \\ x_2 \end{bmatrix} = 0 

This means any vector x = \begin{bmatrix}  x_1 \\ x_2 \end{bmatrix} , where x_2=-x_1  
such as \begin{bmatrix}  1 \\ -1 \end{bmatrix}  is an eigenvector with 
eigenvalue 2. This means eigenspace is given as 
E_2 = span(\begin{bmatrix}  1 \\ -1 \end{bmatrix})

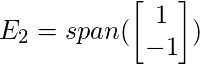
    Los dos espacios propios E_5y E_2en el ejemplo anterior son unidimensionales, ya que cada uno de ellos está atravesado por un solo vector. Sin embargo, en otros casos, podemos tener múltiples vectores propios idénticos y los espacios propios pueden tener más de una dimensión.

    Publicación traducida automáticamente

    Artículo escrito por mkumarchaudhary06 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

    Deja una respuesta

    Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *