Encuentre la posición del término dado en una serie formada con solo los dígitos 4 y 7 permitidos

Hay una serie de números que tienen solo dígitos, 4 y 7, y los números están ordenados en orden creciente. Los primeros números de la serie son 4, 7, 44, 47, 74, 77, 444, etc. Dado un número N , la tarea es encontrar la posición de ese número en la serie dada.
Ejemplos: 
 

Entrada: N = 4 
Salida: 1 
Explicación: 
El primer número de la serie es 4
Entrada: N = 777 
Salida: 14 
Explicación: 
El número 14 de la serie es 777 
 

Enfoque: Este problema se puede resolver utilizando las siguientes observaciones: 
 

• A continuación se muestra el patrón observado en la serie dada. Los números se pueden ver como: 
   

                 ""
              /      \
            4         7
          /   \     /   \ 
        44    47   74    77
       / \   / \   / \  / \

•  
• Como podemos observar, el patrón es creciente en potencia de 2 . Por lo tanto, la idea es iterar sobre los dígitos del número a partir del dígito menos significativo y actualizar la posición del número como: 
  1. Si el dígito actual = 7, entonces agregue 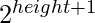 a la posición.
  2. Si el dígito actual = 4, entonces agregue 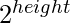 a la posición.
• Imprime la posición final después de las operaciones anteriores.

A continuación se muestra la implementación del enfoque anterior:
 

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the position
// of the number N
void findPosition(int n)
{
    int i = 0;
 
    // To store the position of N
    int pos = 0;
 
    // Iterate through all digit of N
    while (n > 0) {
 
        // If current digit is 7
        if (n % 10 == 7) {
            pos = pos + pow(2, i + 1);
        }
 
        // If current digit is 4
        else {
            pos = pos + pow(2, i);
        }
 
        i++;
        n = n / 10;
    }
 
    // Print the final position
    cout << pos;
}
 
// Driver Code
int main()
{
    // Given number of the series
    int N = 777;
 
    // Function Call
    findPosition(N);
    return 0;
}

// Java program for the above approach
import java.util.*;
class GFG{
 
// Function to find the position
// of the number N
static void findPosition(int n)
{
    int i = 0;
 
    // To store the position of N
    int pos = 0;
 
    // Iterate through all digit of N
    while (n > 0)
    {
 
        // If current digit is 7
        if (n % 10 == 7)
        {
            pos = pos + (int)Math.pow(2, i + 1);
        }
 
        // If current digit is 4
        else
        {
            pos = pos + (int)Math.pow(2, i);
        }
 
        i++;
        n = n / 10;
    }
 
    // Print the final position
    System.out.print(pos);
}
 
// Driver Code
public static void main(String[] args)
{
    // Given number of the series
    int N = 777;
 
    // Function Call
    findPosition(N);
}
}
 
// This code is contributed by shivanisinghss2110

# Python3 program for the above approach
 
# Function to find the position
# of the number N
def findPosition(n):
     
    i = 0
 
    # To store the position of N
    pos = 0
 
    # Iterate through all digit of N
    while (n > 0):
 
        # If current digit is 7
        if (n % 10 == 7):
            pos = pos + pow(2, i + 1)
 
        # If current digit is 4
        else:
            pos = pos + pow(2, i)
             
        i += 1
        n = n // 10
 
    # Print the final position
    print(pos)
 
# Driver Code
if __name__ == '__main__':
     
    # Given number of the series
    N = 777
 
    # Function Call
    findPosition(N)
 
# This code is contributed by mohit kumar 29

// C# program for the above approach
using System;
class GFG{
 
// Function to find the position
// of the number N
static void findPosition(int n)
{
    int i = 0;
 
    // To store the position of N
    int pos = 0;
 
    // Iterate through all digit of N
    while (n > 0)
    {
 
        // If current digit is 7
        if (n % 10 == 7)
        {
            pos = pos + (int)Math.Pow(2, i + 1);
        }
 
        // If current digit is 4
        else
        {
            pos = pos + (int)Math.Pow(2, i);
        }
 
        i++;
        n = n / 10;
    }
 
    // Print the final position
    Console.Write(pos);
}
 
// Driver Code
public static void Main()
{
    // Given number of the series
    int N = 777;
 
    // Function Call
    findPosition(N);
}
}
 
// This code is contributed by Code_Mech

<script>
// javascript program for the above approach
 
    // Function to find the position
    // of the number N
    function findPosition(n)
    {
        var i = 0;
 
        // To store the position of N
        var pos = 0;
 
        // Iterate through all digit of N
        while (n > 0) {
 
            // If current digit is 7
            if (n % 10 == 7) {
                pos = pos + parseInt( Math.pow(2, i + 1));
            }
 
            // If current digit is 4
            else {
                pos = pos + parseInt( Math.pow(2, i));
            }
 
            i++;
            n = parseInt(n / 10);
        }
 
        // Print  the final position
        document.write(pos);
    }
 
    // Driver Code
     
    // Given number of the series
    var N = 777;
 
    // Function Call
    findPosition(N);
 
// This code is contributed by Princi Singh
</script>

14

Complejidad de tiempo: O(log ₁₀ N * log ₂ N) , donde N representa el entero dado.
Espacio auxiliar: O(1) , no se requiere espacio adicional, por lo que es una constante.