ML | Escalado de características – Parte 1

Feature Scaling es una técnica para estandarizar las características independientes presentes en los datos en un rango fijo. Se realiza durante el preprocesamiento de datos. 

Trabajo: 
dado un conjunto de datos con características : edad , salario , apartamento BHK con el tamaño de datos de 5000 personas, cada uno con estas características de datos independientes. 

Cada punto de datos está etiquetado como: 

• Clase 1: SÍ (significa que con la edad , el salario y el valor de la característica del apartamento BHK dados, uno puede comprar la propiedad)
• Class2- NO (significa que con la edad , el salario y el valor de la característica del apartamento BHK dados, uno no puede comprar la propiedad).

Usando un conjunto de datos para entrenar el modelo, uno tiene como objetivo construir un modelo que pueda predecir si uno puede comprar una propiedad o no con valores de características dados. 

Una vez que se entrena el modelo, se puede crear un gráfico N-dimensional (donde N es el número de características presentes en el conjunto de datos) con puntos de datos del conjunto de datos dado. La figura que se muestra a continuación es una representación ideal del modelo.  

Como se muestra en la figura, los puntos de datos de estrellas pertenecen a Clase 1: Sí y los círculos representan etiquetas de Clase 2: No , y el modelo se entrena con estos puntos de datos. Ahora se proporciona un nuevo punto de datos (diamante como se muestra en la figura) y tiene diferentes valores independientes para las 3 características ( edad , salario , apartamento BHK ) mencionadas anteriormente. El modelo tiene que predecir si este punto de datos pertenece a Sí o No. 

Predicción de la clase de nuevos puntos de datos: 
el modelo calcula la distancia de este punto de datos desde el centroide de cada grupo de clase. Finalmente, este punto de datos pertenecerá a esa clase, que tendrá una distancia centroide mínima de él. 
La distancia se puede calcular entre el centroide y el punto de datos utilizando estos métodos: 

• Distancia euclidiana: es la raíz cuadrada de la suma de los cuadrados de las diferencias entre las coordenadas (valores de características: edad , salario , apartamento BHK ) del punto de datos y el centroide de cada clase. Esta fórmula viene dada por el teorema de Pitágoras. 
  
  donde x es el valor del punto de datos, y es el valor del centroide y k es el no. de valores de características, Ejemplo: el conjunto de datos dado tiene k = 3
• Distancia de Manhattan: se calcula como la suma de las diferencias absolutas entre las coordenadas (valores característicos) del punto de datos y el centroide de cada clase. 
  
   
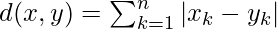
• Distancia de Minkowski: Es una generalización de los dos métodos anteriores. Como se muestra en la figura, se pueden usar diferentes valores para encontrar r.

Necesidad de escalado de características: 
el conjunto de datos proporcionado contiene 3 características: edad , salario , apartamento BHK . Considere un rango de 10-60 para Edad , 1 Lac-40 Lacs para Salario , 1-5 para BHK de Flat . Todas estas características son independientes entre sí. 
Suponga que el centroide de la clase 1 es [40, 22 Lacs, 3] y el punto de datos a predecir es [57, 33 Lacs, 2]. 

Usando el método de Manhattan, 

Distance = (|(40 - 57)| + |(2200000 - 3300000)| + |(3 - 2)|)

Se puede ver que la función Salario dominará todas las demás funciones mientras predice la clase del punto de datos dado y dado que todas las funciones son independientes entre sí, es decir, el salario de una persona no tiene relación con su edad o el requisito del piso. el / ella tiene. Esto significa que el modelo siempre predecirá mal. 

Entonces, la solución simple a este problema es el escalado de características. Los algoritmos de escalado de funciones escalarán la edad, el salario y el BHK en un rango fijo, digamos [-1, 1] o [0, 1]. Y entonces ninguna característica puede dominar a otras.