¿Cómo es que la complejidad temporal de la criba de Eratóstenes es n*log(log(n))?

Pre-requisite: Sieve of Eratosthenes What is Sieve of Eratosthenes algorithm? In order to analyze it, let's take a number n and the task is to print the prime numbers less than n. Therefore, by definition of Sieve of Eratosthenes, for every prime number, it has to check the multiples of the prime and mark it as composite. This process continues until a value p which is the highest prime number less than n. Understanding the n*log(log n) time complexity of Sieve of Eratosthenes

Si se supone que el tiempo necesario para marcar un número como compuesto es constante, entonces el número de veces que se ejecuta el bucle es igual a:

$\frac{n}{2} + \frac{n}{3} + \frac{n}{5} + \frac{n}{7} + ...... p$

Al tomar n común de la ecuación anterior, la ecuación anterior se puede reescribir como: $n \ast (1/2 + 1/3 + 1/5 + 1/7.....\infty )$
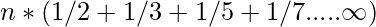
Se puede demostrar de la siguiente manera con la ayuda de la progresión armónica de la suma de números primos : $\frac{1}{2} + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + ...... = log(log(n)$
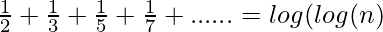
Prueba de progresión armónica de la suma de números primos: Para entender la prueba, el requisito previo es la serie armónica y la expansión de la serie de Taylor .
- Tomemos una ecuación: $log(\frac{x}{1 - x})$
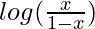
- La expansión en serie de Taylor de la ecuación anterior está dada por: $x + \frac{x^2}{2} + \frac{x^3}{3} + ...$
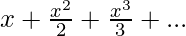
- Poniendo x = 1 en la ecuación anterior, obtenemos la relación: $\sum_1^n \frac{1}{r} = log(n)$ Marquemos la ecuación anterior como 1 .
- De la fórmula del producto de Euler , $\sum_1^\infty \frac{1}{r^{s}} = \prod \frac{1}{1 - p^{-s}}$
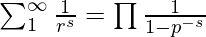
- Al sustituir s = 1 en la ecuación anterior, obtenemos $\sum_1^\infty \frac{1}{r^{1}} = \prod \frac{1}{1 - p^{-1}}$
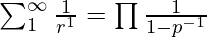
- Al aplicar log a ambos lados: $log(\sum_1^\infty \frac{1}{r^{1}}) = log(\prod \frac{1}{1 - p^{-1}})$
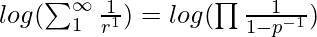
- Al simplificar la ecuación anterior, queda: $log(\sum_1^\infty \frac{1}{r^{1}}) = \sum log( \frac{1}{1 - p^{-1}})$
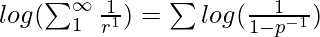
- En la ecuación anterior, 1 > p ^-1 > -1
- Por lo tanto, podemos usar la expansión de la serie de Taylor para el lado derecho de la ecuación anterior. $log( \frac{1}{1-x}) = \sum_1^\infty log( \frac{1}{n * p^{n}})$
- Al sustituir esto en la ecuación anterior, obtenemos: $log( \sum_1^n \frac{1}{r}) = \sum \sum_1^n \frac{1}{n * p^{n}}$ donde p es un número primo.
- Al expandir la suma interna; $\sum_1^n \frac{1}{n * p^{n}} = \frac{1}{p} + \frac{1}{2p^{2}} + \frac{1}{3p^{2}} + .....$
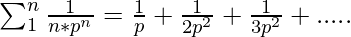
- La serie anterior es convergente. Entonces, la serie anterior se puede aproximar a: $\frac{1}{p}$
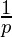
- Por lo tanto, al sustituir y reescribir la ecuación; obtenemos 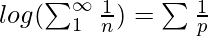$log( \sum_1^\infty \frac{1}{n}) = \sum \frac{1}{p}$ donde p es el número primo.
- De la ecuación inicial 1, finalmente podemos concluir que: 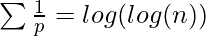$\sum \frac{1}{p} = log(log(n))$ donde p es la suma de los números primos.
Al sustituir esto en la ecuación, obtenemos la complejidad temporal como: $O(n*(log(log(n))))$

Por lo tanto, la complejidad temporal de la Tamiz de Eratóstenes es n*log(log(n)) Referencia: Divergencia de la suma de los recíprocos de los números primos

Publicación traducida automáticamente

Artículo escrito por KaashyapMSK y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta