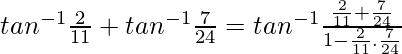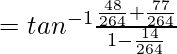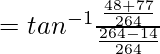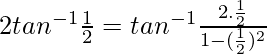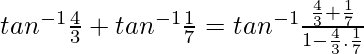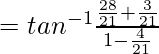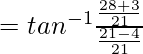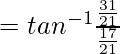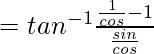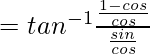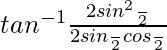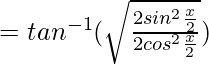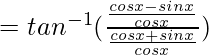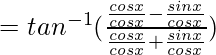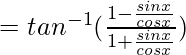Demuestra lo siguiente
Pregunta 1. 3sen -1 x = sen -1 (3x – 4x 3 ), x∈[-1/2, 1/2]
Solución:
Tomemos x = senθ, entonces θ = sen -1 x
Sustituir el valor de x en la ecuación presente en RHS
La ecuación se convierte en sin -1 (3sinθ – 3sin 3 θ)
Sabemos, sin3θ = 3sinθ – 4sin 3 θ
Entonces, sin -1 (3sinθ – 3sin 3 θ) = sin -1 (sin3θ)
Por la propiedad de la trigonometría inversa sabemos, sin(sin -1 (θ)) = θ
Entonces, sen -1 (sen3θ) = 3θ
Y sabemos θ = sen -1 x
Entonces, 3θ = 3sen -1 x = LHS
Pregunta 2. 3cos -1 x = cos -1 (4x 3 – 3x), x∈[-1/2, 1]
Solución:
Tomemos x = cosθ, entonces θ = cos -1 x
Sustituye el valor de x en la ecuación presente en RHS
La ecuación se convierte en cos -1 (4cos 3 θ – 3cosθ)
Sabemos, cos3θ = 4cos 3 θ – 3cosθ
Entonces, cos -1 (4cos 3 θ – 3cosθ) = cos -1 (cos3θ)
Por la propiedad de la trigonometría inversa sabemos, cos(cos -1 (θ)) = θ
Entonces, cos -1 (cos3θ) = 3θ
Y sabemos θ = cos -1 x
Entonces, 3θ = 3cos -1 x = LHS
Pregunta 3.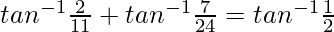
Solución:
Sabemos,
Ahora pon x = 2/11 y y = 7/24
Asi que,
= lado derecho
Pregunta 4. 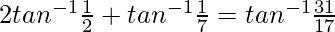
Solución:
Primero tenemos que escribir 2tan -1 x en términos de tan -1 x
Sabemos que 2tan -1 x =
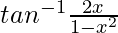
Ponga x = 1/2 en la fórmula anterior
Asi que,
Ahora podemos reemplazar
con
Entonces la ecuación en LHS se convierte en
Sabemos ,
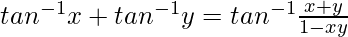
Asi que,
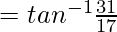
= lado derecho
Escriba las siguientes funciones en sus formas más simples:
Pregunta 5. 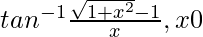
Solución:
Supongamos que x = tanθ, entonces θ = tan -1 x
Sustituye el valor de x en cuestión.
Entonces la ecuación se convierte en
Sabemos que, 1 + tan 2 θ = sec 2 θ
Reemplazando 1 + tan 2 θ con sec 2 θ en la ecuación
Entonces la ecuación se convierte en,
Sabemos, tanθ = sinθ/cosθ y sec = 1/cosθ
Reemplazando el valor de tanθ y secθ en
Sabemos, 1 – cosθ = 2sin 2 θ/2 y sinθ = 2sinθ/2cosθ/2
Entonces, las ecuaciones después de reemplazar el valor anterior se convierten en
Sabemos
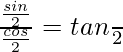
= θ/2 [tan -1 (tanθ) = θ]
= 1/2 bronceado -1 x [θ = bronceado -1 x]
Pregunta 6. 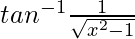 , |x| > 1
, |x| > 1
Solución:
Supongamos que x = cosecθ, entonces θ = cosec -1 x
Sustituye el valor de x en cuestión por
Sabemos que, 1 + cot 2 θ = cosec 2 θ, entonces cosec 2 θ = 1 – cot 2 θ
= tan -1 (tanθ) [1/cotθ = tanθ]
= θ [tan -1 (tanθ) = θ]
= cosec −1 x [θ = cosec −1 x]
= π/2 - seg −1 x [cosec −1 x + seg −1 x = π/2]
Pregunta 7. 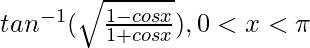
Solución:
Sabemos, 1 – cosx = 2sen 2 x/2 y 1 + cosx = 2cos 2 x/2
Sustituyendo la fórmula anterior en cuestión
= bronceado -1 (tanx/2)
= x/2 [tan -1 (tanθ) = θ]
pregunta 8 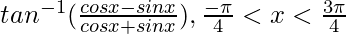
Solución:
Dividir numerador y denominador por
Sabemos,
Esto también se puede escribir como
– (1)
Sabemos
– (2)
Al comparar la ecuación (1) y (2) podemos decir que x = 1 y y = tan -1 x
Entonces podemos decir que
= π/4 – tan −1 x [tan −1 1 = π/4]
Pregunta 9. 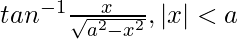
Solución:
Supongamos que x = asinθ, entonces θ = sen -1 x/a
Sustituye el valor de x en cuestión.
Tomando un 2 común del denominador
Sabemos que, sen 2 θ + cos 2 θ = 1, entonces 1 – sen 2 θ = cos 2 θ
= tan -1 (tanθ) [senθ/cosθ = tanθ]
= θ
= sen -1 x/a
Pregunta 10. 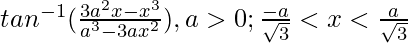
Solución:
Supongamos que x = atanθ, entonces θ = tan -1 x/a
Sustituye el valor de x en cuestión
Sacando un 3 común de numerador y denominador
Sabemos
Asi que,
= 3θ [ tan -1 (tanθ) = θ]
= 3tan -1 x/a
Capítulo 2 Funciones trigonométricas inversas – Ejercicio 2.2 | conjunto 2
Publicación traducida automáticamente
Artículo escrito por pritishnagpal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA