Soluciones NCERT Clase 10 – Capítulo 13 Áreas de superficie y volúmenes – Ejercicio 13.4

Pregunta 1. Un vaso para beber tiene la forma de un tronco de cono de 14 cm de altura. Los diámetros de sus dos extremos circulares son de 4 cm y 2 cm. Encuentre la capacidad del vaso.

Solución:

Valores dados:

Altura del tronco (h) = 14 cm

Radio del extremo del círculo más grande (R) = $\frac{4}{2}$ = 2 cm

Radio del extremo del círculo más pequeño (r) = $\frac{2}{2}$ = 1 cm

Capacidad de vaso troncocónico = Volumen de Frustum

= $\frac{1}{3}$ πh (r2 ⁺ R2 ⁺ rR)

= $\frac{1}{3}$ × π × 14 ((1 × 1) + (2 × 2) × (2 × 1))

= $\frac{1}{3} × \frac{22}{7}$ × 14 × 7 (tomando π= $\frac{22}{7}$ )

= $\frac{(22 × 14)}{3}$

= 102,67 ^cm3

Por lo tanto, la capacidad del vaso troncocónico = 102,67 cm ³

Pregunta 2. La altura inclinada de un tronco de cono es de 4 cm y los perímetros (circunferencia) de sus extremos circulares son de 18 cm y 6 cm. Encuentre el área de la superficie curva del tronco.

Solución:

Altura inclinada del tronco (l) = 4 cm

Deje que el radio del círculo más pequeño termine = r

Deje que el radio del círculo más grande termine = R

Circunferencia del círculo = 2π × (radio del círculo)

Circunferencia del círculo más grande = 2πR

18 cm2 ⁼ 2πR

R = $\frac{18}{2π}$

R = $\frac{9}{π}$ cm

Circunferencia del círculo más pequeño = 2πr

⁶ cm2 = 2πr

r = $\frac{6}{2π}$

r = $\frac{3}{π}$ cm

Ahora, como área de la superficie de la curva de tronco = π (r+R) l

= π × ( $\frac{9}{π}+\frac{3}{π}$ ) × 4

= 12 × 4 (Tomando π común y cancelándolo)

= 48 cm ²

Por lo tanto, el área de la superficie curva del tronco = 48 cm ²

Pregunta 3. Un fez, el gorro usado por los turcos, tiene la forma del tronco de un cono (ver Fig.). Si su radio en el lado abierto es de 10 cm, el radio en la base superior es de 4 cm y su altura inclinada es de 15 cm, encuentre el área del material utilizado para fabricarlo.

Solución:

Valores dados:

Altura inclinada del tronco (l)= 15 cm

Sea el radio del extremo del círculo más pequeño (r) = 4 cm

Deje que el radio del extremo del círculo más grande (R) = 10 cm

Área de material utilizado para su elaboración = Área de la superficie de la curva + área de la base superior

= (π(r+R)l) + (πr ² )

= π ((r+R)l + r ² ) ( Tomando π común )

= π ((4+10) × 15 + (4 × 4))

= $\frac{22}{7}$ × (226) (Tomando π = $\frac{22}{7}$ )

= 710,286 ^cm2

Por lo tanto, el área de material utilizada para fabricarlo = 710.286 cm ²

Pregunta 4. Un recipiente, abierto desde arriba y hecho de una hoja de metal, tiene la forma de un tronco de cono de 16 cm de altura con radios de sus extremos inferior y superior de 8 cm y 20 cm, respectivamente. Encuentre el costo de la leche que puede llenar completamente el recipiente, a razón de ₹ 20 por litro. Halla también el costo de la hoja de metal que se usó para hacer el contenedor, si cuesta ₹ 8 por 100 cm ² . (Tome π = 3.14)

Solución:

Valores dados:

Altura del tronco (h)= 16 cm

Sea el radio del extremo del círculo más pequeño (r) = 8 cm

Deje que el radio del extremo del círculo más grande (R) = 20 cm

La cantidad de leche para llenar el recipiente = Volumen de tronco

= $\frac{1}{3}$ πh (r2 ⁺ R2 ⁺ rR)

= $\frac{1}{3}$ × 3,14 × 16 (8×8 + 20×20 + 8×20) (Tomando π=3,14)

= $\frac{1}{3}$ × 3,14 × 16 × (624)

= 10449,92 cm ³

Costo de 1 litro de leche = ₹ 20

Y como, 1 m ³ = 1000 cm ³ = 1 litro

10449,92 cm3 ⁼ ( $\frac{1}{1000}$ ) ×10449,92 litros

costo de 10449.92 cm ³ = ( $\frac{10449.92}{1000}$ ) × 20

= ₹ 208.998

Ahora, la hoja de metal utilizada para hacer el contenedor = área de la superficie de la curva + área de la base inferior

= (π(r+R)l) + (πr ² )

= π ((r+R)l + r ² ) (Tomando π común)

= π ((20+8) × (√(16 ² +(20-8) ² )) + (8 × 8)) ( Altura inclinada (l) = √(h ² +(Rr) ² ))

= 3,14 × (28 × √400 + 64) (Tomando π = 3,14)

= 3,14 × (624)

= 1959,36 cm ²

Por lo tanto, la hoja de metal utilizada para hacer el recipiente = 1959,36 cm ²

Como, costo de 100 cm ² = ₹ 8

1959,36 cm2 ⁼ (8/100) × 1959,36

= ₹ 156.748

Por lo tanto, el costo de la leche que puede llenar completamente el recipiente = ₹ 208.998

y, el costo de la hoja de metal utilizada para hacer el contenedor = ₹ 156.748

Pregunta 5. Un cono circular recto metálico de 20 cm de altura y cuyo ángulo vertical es de 60° está cortado en dos partes a la mitad de su altura por un plano paralelo a su base. Si el tronco así obtenido se estira en un alambre de 1/16 cm de diámetro, encuentre la longitud del alambre.

Solución:

Como el ángulo se corta en dos partes iguales, la altura también se reduce a la mitad.

Deje que el radio del círculo más pequeño termine = r

Deje que el radio del círculo más grande termine = R

En ∆PFR y ∆PEB

bronceado ∝ = $\frac{(opposite \hspace{0.1cm}side)}{(adjacent \hspace{0.1cm}side)}$

bronceado 30° = $\frac{EB}{PE} = \frac{FR}{PF}$

$\frac{1}{√3} = \frac{r} {10} = \frac{R}{20}$

R = $\frac{20}{√3}$

r = $\frac{10}{√3}$

y como altura del tronco = 10 cm

Entonces, de acuerdo con la pregunta,

Frustum se convierte en alambre cilíndrico con diámetro $\mathbf{\frac{1}{16}}$ cm

Volumen de Frustum = Volumen de Cilindro

Volumen de Frustum = $\frac{1}{3}$ πh (r ² + R ² + rR)

= $\frac{1}{3} × π × 10 (\frac{10}{√3} × \frac{10}{√3} + \frac{20}{√3} × \frac{20}{√3} + \frac{20}{√3} × \frac{10}{√3})$

= $\frac{1}{3} × π × 10 × (\frac{100}{3} + \frac{400}{3} + \frac{200}{3})$

= $\frac{1}{3} × π × 10 × \frac{700}{3}$

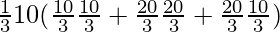
= $\frac{7000π}{ 9}$ cm3 ………………………..(1 ⁾

Volumen del cilindro = $\frac{1}{3}$ π(radio) ² H

= $\frac{1}{3}$ π( $\frac{1}{16×2}$ ) ² H …………………(2)

Como (1) = (2), entonces

7000π / 9 = 1/3 π(1/(16×2)) ² H

H = $\frac{7000π × 32 × 32}{9 × π}$ (cancelar π de ambos lados)

altura = 796444,443 cm

altura = 7964,44 m

Por lo tanto, la longitud del cable = 7964,44 m