Suma de todos los números palindrómicos de N dígitos divisibles por 9 formados con los dígitos del 1 al 9

Dado un número N , la tarea es encontrar la suma de todos los números palindrómicos de N dígitos (formados por dígitos del 1 al 9) que son divisibles por 9. Ejemplos:

Entrada: N = 1 Salida: 9 Explicación: Solo 9 es un número palindrómico de 1 dígito divisible por 9 Entrada: N = 3 Salida: 4995 Explicación: Los números palindrómicos de tres dígitos divisibles por 9 son: 171, 252, 333, 414, 585, 666, 747, 828, 999

Enfoque: La observación clave en el problema es que si un número es divisible por 9, entonces la suma de los dígitos de ese número también es divisible por 9 . Otra observación es que si contamos el número de números palindrómicos de N dígitos usando los dígitos del 1 al 9, entonces se puede observar que

Ocurrencia de cada dígito = (recuento de números de N dígitos / 9)

Por lo tanto,

Primero encuentre el conteo de números palindrómicos de N dígitos divisibles por 9, como: $\text{Recuento de números palindrómicos de N dígitos divisibles por 9} = \begin{casos} 9^{\frac{N-1}{2}} & \text{si N es impar} \\ 9^{\frac {N-2}{2}} & \text{ si N es par} \end{cases}$
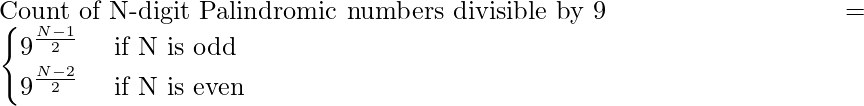
Entonces, si N es 1 o 2, la suma será simplemente 9 y 99 respectivamente, ya que son los únicos números palindrómicos de 1 y 2 dígitos.
Si N > 2, entonces la suma de números palindrómicos de N-ésimo dígito divisibles por 9 es \text{Suma de números palindrómicos de N-ésimo dígito divisibles por 9 }= (\text{suma de }(N-1)^{th}\text{ dígito } * 10) + (5*\text{ recuento de números palindrómicos de N dígitos divisibles por 9})

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ implementation to find the sum
// of all the N digit palindromic
// numbers divisible by 9
 
#include <bits/stdc++.h>
 
using namespace std;
 
// Function for finding count of
// N digits palindrome which
// are divisible by 9
int countPalindrome(int n)
{
    int count;
 
    // if N is odd
    if (n % 2 == 1) {
        count = pow(9, (n - 1) / 2);
    }
    // if N is even
    else {
        count = pow(9, (n - 2) / 2);
    }
    return count;
}
 
// Function for finding sum of N
// digits palindrome which are
// divisible by 9
int sumPalindrome(int n)
{
    // count the possible
    // number of palindrome
    int count = countPalindrome(n);
 
    int res = 0;
 
    if (n == 1)
        return 9;
    if (n == 2)
        return 99;
 
    for (int i = 0; i < n; i++) {
        res = res * 10 + count * 5;
    }
 
    return res;
}
 
// Driver Code
int main()
{
    int n = 3;
    cout << sumPalindrome(n);
    return 0;
}

Java

// Java implementation to find the sum
// of all the N digit palindromic
// numbers divisible by 9
import java.util.*;
 
class GFG{
     
// Function for finding count of
// N digits palindrome which
// are divisible by 9
static int countPalindrome(int n)
{
    int count;
 
    // If N is odd
    if (n % 2 == 1)
    {
        count = (int)Math.pow(9, (n - 1) / 2);
    }
     
    // If N is even
    else
    {
        count = (int)Math.pow(9, (n - 2) / 2);
    }
    return count;
}
 
// Function for finding sum of N
// digits palindrome which are
// divisible by 9
static int sumPalindrome(int n)
{
     
    // Count the possible
    // number of palindrome
    int count = countPalindrome(n);
 
    int res = 0;
 
    if (n == 1)
        return 9;
    if (n == 2)
        return 99;
 
    for(int i = 0; i < n; i++)
    {
    res = res * 10 + count * 5;
    }
 
    return res;
}
 
// Driver Code
public static void main(String[] args)
{
    int n = 3;
     
    System.out.println(sumPalindrome(n));
}
}
 
// This code is contributed by ANKITKUMAR34

Python3

# Python3 implementation to find the
# sum of all the N digit palindromic
# numbers divisible by 9
 
# Function for finding count of
# N digits palindrome which
# are divisible by 9
def countPalindrome(n):
 
    count = 0
     
    # If N is odd
    if (n % 2 == 1):
        count = pow(9, (n - 1) // 2)
         
    # If N is even
    else:
        count = pow(9, (n - 2) // 2)
         
    return count
 
# Function for finding sum of N
# digits palindrome which are
# divisible by 9
def sumPalindrome(n):
 
    # Count the possible
    # number of palindrome
    count = countPalindrome(n)
 
    res = 0
 
    if (n == 1):
        return 9
    if (n == 2):
        return 99
 
    for i in range(n):
        res = res * 10 + count * 5
 
    return res
 
# Driver Code
n = 3
 
print(sumPalindrome(n))
 
# This code is contributed by ANKITKUMAR34

C#

// C# implementation to find the sum
// of all the N digit palindromic
// numbers divisible by 9
using System;
 
class GFG{
     
// Function for finding count of
// N digits palindrome which
// are divisible by 9
static int countPalindrome(int n)
{
    int count;
 
    // If N is odd
    if (n % 2 == 1)
    {
        count = (int)Math.Pow(9, (n - 1) / 2);
    }
     
    // If N is even
    else
    {
        count = (int)Math.Pow(9, (n - 2) / 2);
    }
    return count;
}
 
// Function for finding sum of N
// digits palindrome which are
// divisible by 9
static int sumPalindrome(int n)
{
     
    // Count the possible
    // number of palindrome
    int count = countPalindrome(n);
 
    int res = 0;
 
    if (n == 1)
        return 9;
    if (n == 2)
        return 99;
 
    for(int i = 0; i < n; i++)
    {
    res = res * 10 + count * 5;
    }
 
    return res;
}
 
// Driver Code
public static void Main(String[] args)
{
    int n = 3;
     
    Console.WriteLine(sumPalindrome(n));
}
}
 
// This code is contributed by Amit Katiyar

Javascript

// JavaScript implementation to find the sum
// of all the N digit palindromic
// numbers divisible by 9
 
// Function for finding count of
// N digits palindrome which
// are divisible by 9
function countPalindrome(n)
{
    let count;
 
    // if N is odd
    if (n % 2 == 1) {
        count = Math.pow(9, (n - 1) / 2);
    }
    // if N is even
    else {
        count = Math.pow(9, (n - 2) / 2);
    }
    return count;
}
 
// Function for finding sum of N
// digits palindrome which are
// divisible by 9
function sumPalindrome(n)
{
    // count the possible
    // number of palindrome
    let count = countPalindrome(n);
 
    let res = 0;
 
    if (n == 1)
        return 9;
    if (n == 2)
        return 99;
 
    for (var i = 0; i < n; i++) {
        res = res * 10 + count * 5;
    }
 
    return res;
}
 
// Driver Code
let n = 3;
console.log(sumPalindrome(n));
 
// This code is contributed by phasing17

Salida :

4995

Complejidad de tiempo: O (log ₉ n)

Espacio Auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por ApurvaRaj y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta