Soluciones NCERT Clase 8 – Capítulo 12 Exponentes y Potencias – Ejercicio 12.1

Pregunta 1. Evaluar:

Solución:

(yo) 3 ^–2

3 ^-2 = (Propiedad utilizada: a ^-n = ) $\frac{1}{(3^2)} = \frac{1}{9}$    $\frac{1}{a^n}$

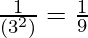
(ii) (– 4) ^{– 2}

(-4) ^-2 = (Propiedad utilizada: a ^-n = ) $\frac{1}{(-4)^2} = \frac{1}{16}$    $\frac{1}{a^n}$

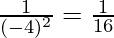
(iii) ( $\frac{1}{2}$ ) ^-5

( $\frac{1}{2}$ ) ^-5 = (2) ⁵ = 32   (Propiedad utilizada: $(\frac{b}{a})^{-n} = \frac{a^n}{b^n}$ )

Pregunta 2. Simplifique y exprese el resultado en notación de potencia con un exponente positivo.

Solución:

(i) (-4) ⁵ ÷ (-4) ⁸

= (-4) ^5-8 = (-4) ^-3 (Propiedad utilizada: a ^m ÷ a ⁿ = a ^m-n )

= $\frac{1}{(-4)^3}$

= $\mathbf{(\frac{1}{(-4)})^3}$

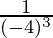
(ii) $(\frac{1}{2^3})^2$

= (Propiedad utilizada: (a ^m ) ⁿ = a ^m×n ) $\frac{(1)^2}{(2^3)^2}$

= $\frac{1}{2^6}$

= $\mathbf{\frac{1}{2^6}}$

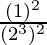
(iii) (-3) ⁴ × ( $\frac{5}{3}$ ) ⁴

= ((3) ⁴ × (Propiedad utilizada: (a/b) ⁿ = a ⁿ / b ⁿ & (-a) ⁿ = a ⁿ si a es un número positivo y n es par) $\frac{5^4}{3^4}$

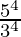
= 5 ⁴

(iv) (3 ^-7 ÷ 3 ^-10 ) × 3 ^-5

= 3 ^(-7-(-10)) × 3 ^-5(Propiedad utilizada: a ^m ÷ a ⁿ = a ^m-n )

= 3 ^(-7+10) × 3 ^-5

= 3 ³ × 3 ^-5

= 3 ^(3+(-5))(Propiedad utilizada: a ^m × a ⁿ = a ^{m + n} )

= 3 ^-2(Propiedad utilizada: a ^-m = $\frac{1}{a^m}$ )

= $\frac{1}{3^2}$

= $\mathbf{\frac{1}{3^2}}$

(v) 2 ^-3 × (-7) ^-3

= (2 × (-7)) ^-3(Propiedad utilizada: a ^m × b ^m = (a×b) ^m )

= (-14) ^-3(Propiedad utilizada: a ^-m = $\frac{1}{a^m}$ )

= $\frac{1}{(-14)^3}$

= $\mathbf{\frac{1}{(-14)^3}}$

Pregunta 3. Encuentra el valor de

Solución:

(i) (3 ⁰ + 4 ^-1 ) × 2 ²

= (1 + ( $\frac{1}{4}$ )) × 4 (un ⁰ = 1 un ≠ 0)

= ( $\frac{5}{4}$ ) × 4

= 5

(ii) (2 ^-1 × 4 ^-1 ) ÷ 2 ^-2

= (2 × 4) ^-1 ÷ (Propiedad utilizada: a ^m × b ^m = (a×b) ^m ) $\frac{1}{2^2}$

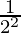
= (8)-1 ÷ $\frac{1}{4}$

= ( $\frac{1}{8}$ ) ÷ $\frac{1}{4}$

=( $\frac{1}{8}$ ) × 4

= ( $\frac{1}{2}$ )

(iii) (1/2) ^-2 + (1/3) ^-2 + (1/4) ^-2

= 2 ² + 3 ² + 4 ²(Propiedad utilizada: $(\frac{1}{a})^{-m}$ =a ^m )

= 4 + 9 + 16

= 29

(iv) (3 ^-1 + 4 ^-1 + 5 ^-1 ) ⁰

= ( $\frac{1}{3} + \frac{1}{4} + \frac{1}{5}$ ) ⁰(un ⁰ = 1 (un ≠ 0)

= 0

(v) {( $\frac{-2}{3}$ ) ^-2 } ²

= ( $\frac{-2}{3}$ ) ^-2×2(Propiedad utilizada: (a ^m ) ⁿ = a ^m×n )

= ( $\frac{-2}{3}$ ) ^-4 = ( $\frac{-3}{2}$ ) ⁴(Propiedad utilizada: (b/a) ^-n = a ⁿ /b ⁿ )

= $\frac{3^4}{2^4}$

= $\frac{81}{16}$

Pregunta 4. Evaluar

Solución:

(i) (8 ^-1 × 5 ³ ) / 2 ^-4

= ( $\frac{1}{8}$ × 125) / (2 ^-4 ) (Propiedad utilizada: (b/a) ^-n = a ⁿ /b ⁿ )

= ( $\frac{1}{8}$ ) × 125 × 2 ⁴

= 250

(ii) (5 ^-1 × 2 ^-1 ) × 6 ^-1

= (5 × 2) ^-1 × 6 ^-1 (Propiedad utilizada: a ^m × b ^m = (a×b) ^m )

= 10 ^-1 × 6 ^-1

= (10 × 6) ^-1(Propiedad utilizada: a ^m × b ^m = (a×b) ^m )

= 60 ^-1

= $\frac{1}{60}$

Pregunta 5. Encuentra el valor de m para el cual 5 ^m ÷ 5 ^{– 3} = 5 ⁵

Solución:

5 ^{m-(– 3)} = 5 ⁵ (Propiedad utilizada: a ^m ÷ a ⁿ = a ^m-n )

5m ⁺³ = 5 ⁵

m+3 = 5

m = 5-3

metro = 2

Pregunta 6. Evaluar

Solución:

(yo) {( $\frac{1}{3}$ ) ^-1 – ( $\frac{1}{4}$ ) ^-1 } ^-1

= (3 ¹ – 4 ¹ ) ^-1(Propiedad utilizada: (1/a) ^-m = a ^m )

= (-1) ^-1

= (1/(-1)) ¹

= (-1)

(ii) ( $\frac{5}{8}$ ) ^-7 × ( $\frac{8}{5}$ ) ^-4

= ( $\frac{5}{8}$ ) ⁷ × ( $\frac{8}{5}$ ) ^-4(Propiedad utilizada: (b/a) ^-n = (a/b) ⁿ )

= ( $\frac{8}{5}$ ) ^{7+ (-4)}(Propiedad utilizada: a ^m × a ⁿ = a ^{m + n} )

= ( $\frac{8}{5}$ ) ³ = 8 ³ /5 ³

= $\frac{512}{125}$

Pregunta 7. Simplifica

Solución:

(yo) $\frac{(25 \times t^{-4})}{(5^{-3} \times 10 \times t^{-8})}$ (t ≠ 0)

= $\frac{(5^2 \times t^{-4})}{(5^{-3} \times 10 \times t^{-8})}$ (Propiedad utilizada: a ^m ÷ a ⁿ = a ^m-n ) (25 = 5 ² )

= $\frac{(5^{2-(-3)} \times t^{-4-(-8)})}{ 10}$

= $\frac{(5^{5} \times t^{4})}{ 10}$

= $\frac{(625 \times t^{4})}{ 2}$

(ii) $\frac{(3^{-5} \times 10^{-5} \times 125)}{(5^{-7} \times 6^{-5})}$

= $\frac{(3^{-5} \times (2\times 5)^{-5} \times 125)}{(5^{-7} \times (2 \times 3)^{-5})}$

= $\frac{(3^{-5} \times 2^{-5}\times 5^{-5} \times 125)}{(5^{-7} \times 2^{-5} \times 3^{-5})}$ (Propiedad utilizada: (a×b) ^m = a ^m × b ^m )

= (3 ^-5-(-5) × 2 ^-5-(-5) × 5 ^(-5)+3+7 ) (Propiedad utilizada: a ^m ÷ a ⁿ = a ^m-n )

= (3 ⁰ × 2 ⁰ × 5 ⁵ ) (un ⁰ = 1 (un ≠ 0)

= 5 ⁵