Soluciones NCERT de Clase 8 – Capítulo 3 Comprender los cuadriláteros – Ejercicio 3.3

Pregunta 1. Dado un paralelogramo ABCD. Complete cada afirmación junto con la definición o propiedad utilizada.

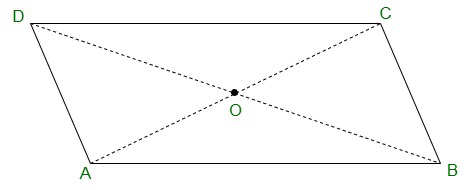
(i) DA = …… 

(ii) ∠DCB = ……

(iii) CO = …… 

(iv) m ∠DAB + m ∠CDA = ……

Solución:

(i) AD = BC {Los lados opuestos de un paralelogramo son iguales}

(ii) ∠DCB = ∠DAB {Los ángulos opuestos de un paralelogramo son iguales} 

(iii) OC = OA {Las diagonales de un paralelogramo son iguales}

(iv) m ∠DAB + m ∠CDA = 180°

Pregunta 2. Considera los siguientes paralelogramos. Encuentra los valores de las incógnitas x, y, z

Solución:

(i)

y = 100° {ángulos opuestos de un paralelogramo}

x + 100° = 180° {Ángulos adyacentes de un paralelogramo}

⇒ x = 180° – 100° 
⇒ x = 80°

x = z = 80° {ángulos opuestos de un paralelogramo}

Por lo tanto, 

x = 80°, y = 100° y z = 80°

(ii)

50° + x = 180° 

⇒ x = 180° – 50° = 130° {Ángulos adyacentes de un paralelogramo} 

⇒ x = y = 130° {ángulos opuestos de un paralelogramo}

⇒ x = z = 130° {ángulo correspondiente}

(iii)

x = 90° {ángulos verticales opuestos}

x + y + 30° = 180° {propiedad de la suma de los ángulos de un triángulo}

⇒ 90° + y + 30° = 180°

⇒ y = 180° – 120° = 60°

también, y = z = 60° {ángulos alternos}

(iv)

z = 80° {ángulo correspondiente} 

z = y = 80° {ángulos alternos} 

x + y = 180° {ángulos adyacentes}

⇒ x + 80° = 180° 

⇒ x = 180° – 80° = 100°

(v)

y = 112° {ángulos opuestos de un paralelogramo}

x = 180° – (y + 40°) {propiedad de la suma de los ángulos de un triángulo}

x = 28°

z = 28° {ángulos alternos}

Pregunta 3. ¿Puede un cuadrilátero ABCD ser un paralelogramo si 

(i) ∠D + ∠B = 180°?

(ii) AB = DC = 8 cm, AD = 4 cm y BC = 4,4 cm?

(iii)∠A = 70° y ∠C = 65°?

Solución:

(yo) Sí, 

El cuadrilátero ABCD será un paralelogramo si ∠D + ∠B = 180°,

también debe cumplir algunas condiciones que son:

(a) La suma de los ángulos adyacentes debe ser 180°.

(b) Los ángulos opuestos deben ser iguales.

(ii) No, los lados opuestos deben tener la misma longitud. 

Aquí, AD ≠ BC

(iii) No, los ángulos opuestos deben tener las mismas medidas. 

Aquí, ∠A ≠ ∠C

Pregunta 4. Dibuja una figura aproximada de un cuadrilátero que no sea un paralelogramo pero que tenga exactamente dos ángulos opuestos de igual medida.

Solución:

ABCD es una figura de cuadrilátero que no es un paralelogramo pero tiene exactamente dos ángulos opuestos 

eso es ∠B = ∠D de igual medida. No es un paralelogramo porque ∠A ≠ ∠C.

Pregunta 5. Las medidas de dos ángulos adyacentes de un paralelogramo están en la razón 3:2. Halla la medida de cada uno de los ángulos del paralelogramo.

Solución:

Sean las medidas de dos ángulos adyacentes ∠A y ∠B 3x y 2x respectivamente en el paralelogramo ABCD.

∠A + ∠B = 180°

⇒ 3x + 2x = 180°

⇒ 5x = 180°

⇒ x = 36°

Como sabemos, los lados opuestos de un paralelogramo son iguales.

∠A = ∠C = 3x = 3 × 36° = 108°

∠B = ∠D = 2x = 2 × 36° = 72°

Pregunta 6. Dos ángulos adyacentes de un paralelogramo tienen la misma medida. Halla la medida de cada uno de los ángulos del paralelogramo.

Solución:

Sea ABCD un paralelogramo.

La suma de los ángulos adyacentes de un paralelogramo = 180°

∠A + ∠B = 180°

⇒ 2∠A = 180°

⇒ ∠A = 90°

además,

90° + ∠B = 180°

⇒ ∠B = 180° – 90° = 90°

∠A = ∠C = 90°

∠B = ∠D = 90°

Pregunta 7. La figura adyacente ESPERANZA es un paralelogramo. Halla las medidas de los ángulos x, y y z. Indique las propiedades que usa para encontrarlos.

Solución:

y = 40° {ángulo interior alterno}

∠P = 70° {ángulo interior alterno}

∠P = ∠H = 70° {ángulos opuestos de un paralelogramo}

z = ∠H – 40°= 70° – 40° = 30°

∠H + x = 180°

⇒ 70° + x = 180°

⇒ x = 180° – 70° = 110°

Pregunta 8. Las siguientes figuras GUNS y RUNS son paralelogramos. Encuentre x e y. (Las longitudes están en cm)

Solución:

(i)

SG = NU y SN = GU {los lados opuestos de un paralelogramo son iguales} 

3x = 18

x = 18/3

⇒x =6

3y – 1 = 26 y,

⇒ 3y = 26 + 1

⇒ y = 27/3=9

x = 6 y y = 9

(ii)

20 = y + 7 y 16 = x + y {las diagonales de un paralelogramo se bisecan entre sí} 

y + 7 = 20

⇒ y = 20 – 7 = 13 y,

x + y = 16

⇒ x + 13 = 16

⇒ x = 16 – 13 = 3

x = 3 y y = 13

Pregunta 9. En la figura anterior , tanto RIESGO como PISTA son paralelogramos. Encuentra el valor de x.

Solución:

∠K + ∠R = 180° {los ángulos adyacentes de un paralelogramo son suplementarios}

⇒ 120° + ∠R = 180°

⇒ ∠R = 180° – 120° = 60°

también, ∠R = ∠SIL {ángulos correspondientes}

⇒ ∠SIL = 60°

además, 

∠ECR = ∠L = 70° {ángulos correspondientes} 

x + 60° + 70° = 180° {suma de los ángulos de un triángulo}

⇒ x + 130° = 180°

⇒ x = 180° – 130° = 50°

Pregunta 10. Explica cómo esta figura es un trapecio. ¿Cuál de sus dos lados es paralelo? (Figura)

Solución:

Cuando una recta transversal corta a dos rectas de tal manera que la suma de los ángulos adyacentes del mismo lado de la transversal es 180°, entonces, las rectas son paralelas entre sí.

Aquí tenemos, ∠M + ∠L = 100° + 80° = 180°

Por lo tanto, MN || L.K.

Como el cuadrilátero KLMN tiene un par de líneas paralelas, es un trapecio. 

MN y LK son rectas paralelas.

Pregunta 11. Encuentra m∠C en la figura si AB || ¿CORRIENTE CONTINUA?

Solución:

m∠C+ m∠B = 180° {ángulos del mismo lado de la transversal}

⇒ m∠C+ 120° = 180°

⇒ m∠C = 180° − 120° = 60°

Pregunta 12. Encuentra la medida de ∠P y ∠S si SP || ¿RQ? En figura. (Si encuentra m∠R, ¿hay más de un método para encontrar m∠P?)

Solución:

∠P + ∠Q = 180° {ángulos del mismo lado de la transversal}

⇒ ∠P + 130° = 180°

⇒ ∠P = 180° – 130° = 50°

además, 

∠R + ∠S = 180° {ángulos del mismo lado de la transversal}

⇒ 90° + ∠S = 180°

⇒ ∠S = 180° – 90° = 90°

Por lo tanto, ∠P = 50° y ∠S = 90°

Sí, hay más de un método para encontrar m∠P.

PQRS es un cuadrilátero. La suma de las medidas de todos los ángulos de un cuadrilátero es 360°.

Así, como conocemos la medida de ∠Q, ∠R y ∠S.

∠Q = 130°, ∠R = 90° y ∠S = 90°

∠P + 130° + 90° + 90° = 360°

⇒ ∠P + 310° = 360°

⇒ ∠P = 360° – 310° = 50°