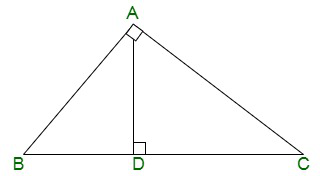
Pregunta 11. En la siguiente figura, E es un punto del lado CB producido a partir de un triángulo isósceles ABC con AB = AC. Si AD ⊥ BC y EF ⊥ AC, demuestre que ΔABD ~ ΔECF.
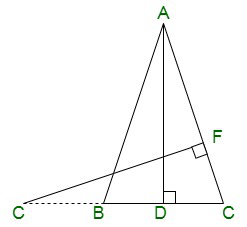
Solución:
Dado, ABC es un triángulo isósceles.
Como los lados de un triángulo isósceles son iguales, tenemos,
∴ AB = CA
⇒ ∠ABD = ∠ECF
En ΔABD y ΔECF,
Ya que, cada uno de los siguientes ángulos son 90°.
∠ADB = ∠EFC
Como ya hemos probado,
∠MALO = ∠CEF
Por el criterio de similitud AA, tenemos,
∴ ΔABD ~ ΔECF
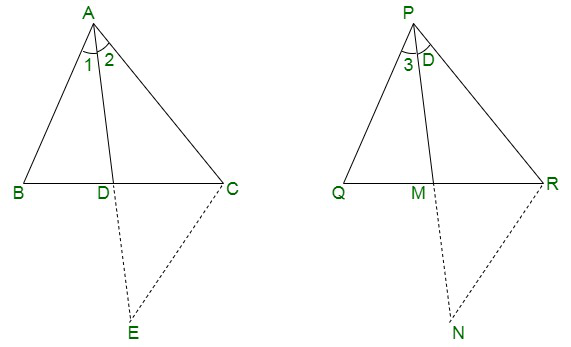
Pregunta 12. Los lados AB y BC y la mediana AD de un triángulo ABC son respectivamente proporcionales a los lados PQ y QR y la mediana PM de ΔPQR (ver Fig. 6.41). Demuestre que ΔABC ~ ΔPQR.
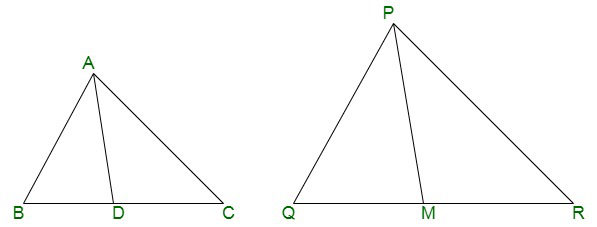
Solución:
Dado que en ΔABC y ΔPQR,
AB es proporcional a PQ
BC es proporcional a QR
AD es proporcional a PM
Es decir, AB/PQ = BC/QR = AD/PM
Sabemos,
AB/PQ = BC/QR = AD/PM
Dado que D es el punto medio de BC y M es el punto medio de QR
⇒AB/PQ = BC/QR = AD/PM
Por el criterio de similitud SSS, tenemos,
⇒ ΔABD ~ ΔPQM
Ahora, como los ángulos correspondientes de dos triángulos semejantes son iguales, obtenemos,
∴ ∠ABD = ∠PQM
⇒ ∠ABC = ∠PQR
Ahora,
En ΔABC y ΔPQR
AB/PQ = BC/QR ………….(i)
∠ABC = ∠PQR ……………(ii)
De la ecuación (i) y (ii), obtenemos,
Por el criterio de similitud SAS, tenemos,
ΔABC ~ ΔPQR
Pregunta 13. D es un punto en el lado BC de un triángulo ABC tal que ∠ADC = ∠BAC. Demostrar que CA2 = CB.CD
Solución:
Dado, D es un punto en el lado BC de un triángulo ABC tal que ∠ADC = ∠BAC.
En ΔADC y ΔBAC,
∠CAD = ∠BAC
∠ACD = ∠BCA (ángulos comunes)
Por el criterio de similitud AA, tenemos,
∴ ΔADC ~ ΔBAC
Como los lados correspondientes de triángulos semejantes están en proporción, obtenemos,
∴ CA/CB = CD/CA
Es decir, CA 2 = CB.CD.
Por lo tanto, probado.
Pregunta 14. Los lados AB y AC y la mediana AD de un triángulo ABC son respectivamente proporcionales a los lados PQ y PR ya la mediana PM de otro triángulo PQR. Demuestre que ΔABC ~ ΔPQR.
Solución:
Dados, Dos triángulos ΔABC y ΔPQR en los que AD y PM son medianas tales que;
Ahora,
AB/PQ = AC/PR = AD/PM
Construcción,
Produzca AD más allá de E de modo que AD = DE. Ahora, únete a CE.
De manera similar, produzca PM más hasta N tal que PM = MN. Únete a RN.
En ΔABD y ΔCDE, tenemos
De la construcción hecha,
AD = DE
Ahora, como AP es la mediana,
BD = CC
y, ∠ADB = ∠CDE [Los ángulos verticalmente opuestos son iguales]
Por criterio SAS,
∴ ΔABD ≅ ΔCDE
Por CPCT, tenemos,
⇒ AB = CE………………..(i)
En ΔPQM y ΔMNR,
De la construcción hecha,
PM = MN
Ahora, como PM es la mediana,
QM = MR
y, ∠PMQ = ∠NMR [Los ángulos verticalmente opuestos son iguales]
Por criterio SAS,
∴ ΔPQM = ΔMNR
por CPCT,
⇒ PQ = RN …………………(ii)
Ahora, AB/PQ = AC/PR = AD/PM
De la ecuación (i) y (ii), concluimos,
⇒CE/RN = AC/PR = AD/PM
⇒ CE/RN = AC/PR = 2AD/2PM
Sabemos,
2AD = AE y 2PM = PN.
⇒ CE/RN = AC/PR = AE/PN
Por criterio de similitud SSS,
∴ ΔACE ~ ΔPRN
De este modo,
∠2 = ∠4
Y, ∠1 = ∠3
∴ ∠1 + ∠2 = ∠3 + ∠4
⇒ ∠A = ∠P ………………….(iii)
Ahora, en ΔABC y ΔPQR, tenemos
AB/PQ = AC/PR [Dado]
De la ecuación (iii), tenemos,
∠A = ∠P
Por criterio de similitud SAS,
∴ ΔABC ~ ΔPQR
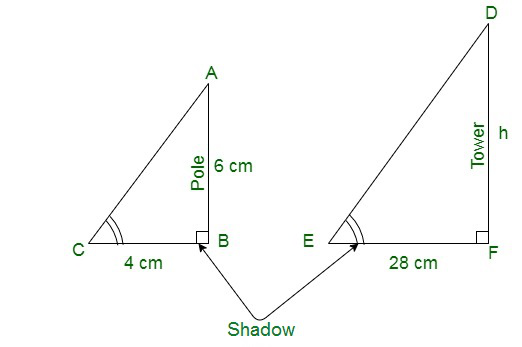
Pregunta 15. Un poste vertical de 6 m de largo proyecta una sombra de 4 m de largo sobre el suelo y al mismo tiempo una torre proyecta una sombra de 28 m de largo. Encuentra la altura de la torre.
Solución:
Dado, Longitud del poste vertical = 6m
Longitud de la sombra de la torre = 28 m
Sombra del poste = 4 m
Supongamos que la altura de la torre es h m.
En ΔABC y ΔDEF,
∠C = ∠E (Por elevación angular de la suma)
Ya que los siguientes ángulos son equivalentes a 90°
∠B = ∠F
Por el criterio de similitud AA, tenemos,
∴ ΔABC ~ ΔDEF
Ya que, si dos triángulos son semejantes los lados correspondientes son proporcionales
∴ AB/DF = BC/EF
Sustituyendo valores,
∴ 6/hora = 4/28
⇒h = (6×28)/4
⇒ h = 6 × 7
⇒ h = 42 metros
Por lo tanto, la altura de la torre especificada es de 42 m.
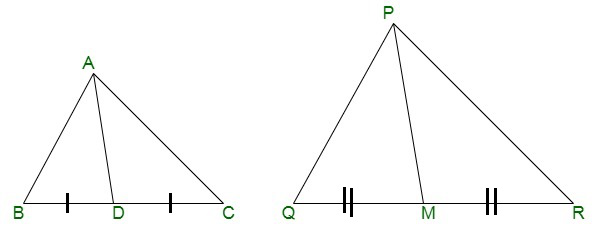
Pregunta 16. Si AD y PM son medianas de los triángulos ABC y PQR, donde ΔABC ~ ΔPQR respectivamente, demuestre que AB/PQ = AD/PM.
Solución:
Dado, ΔABC ~ ΔPQR
Ya que, los lados correspondientes de triángulos semejantes están en proporción.
∴ AB/PQ = AC/PR = BC/QR………………(i)
Y, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R ………….…..(ii)
Dado que AD y PM son las medianas, dividirán sus lados opuestos de manera correspondiente.
∴ BD = BC/2 y QM = QR/2 ………….(iii)
De las ecuaciones (i) y (iii), obtenemos,
AB/PQ = BD/QM …………….(iv)
En ΔABD y ΔPQM,
De la ecuación (ii), tenemos
∠B = ∠Q
De la ecuación (iv), tenemos,
AB/PQ = BD/QM
Por el criterio de similitud SAS, tenemos,
∴ ΔABD ~ ΔPQM
Es decir, AB/PQ = BD/QM = AD/PM
Publicación traducida automáticamente
Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA