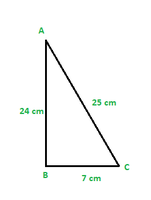
Pregunta 1. En ∆ ABC, rectángulo en B, AB = 24 cm, BC = 7 cm. Determinar :
(i) sen A, cos A (ii) sen C, cos C
Solución:
Usando el teorema de Pitágoras para ΔABC
CA 2 = AB 2 + BC 2
= (24 cm) 2 + (7 cm) 2
= (576 + 49) cm2
= 625cm2
∴CA = 25 cm
(i) sen A = opp/hyp
sen A = 7/25
cos A = adj/hip = 24/25
porque A = 24/25
(ii) sen C = opp/hyp
sen C = 24/25
porque C = adj./hip.
porque C = 7/25
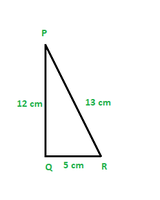
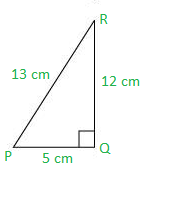
Pregunta 2. En la figura 8.13, encuentre tan P – cot R.
Solución:
Aplicando el teorema de Pitágoras para ΔPQR, obtenemos
PR 2 = PQ 2 + QR 2
(13 cm) 2 = (12 cm) 2 + QR 2
169 cm 2 = 144 cm 2 + QR 2
25 cm 2 = QR 2
QR = 5 cm
bronceado P = opp/adj
bronceado P = 5/12
cuna R = adj/opp
cuna R = 5/12
bronceado P – cuna R = 5/12 – 5/12 = 0
Pregunta 3. Si sen A = 3/4, calcula cos A y tan A.
Solución:
Usando sen 2 A + cos 2 A = 1
(3/4) 2 + cos 2 A = 1
cos 2 A = 1 – (3/4) 2 = 1 – 9/16
porque A = 7 1/2 /4
tan A = sen A/cos A
tan A = (3/4)/(7 1/2 /4)
bronceado A = 3/7 1/2
Pregunta 4: Dado 15 cot A = 8. Encuentra sen A y sec A
Solución:
Dado, 15 cot A = 8
cuna A = 8/15
bronceado A = 1/cuna A
bronceado A = 15/8
Usando, 1 + tan 2 A = seg 2 A
1 + (15/8) 2 = seg 2 A
289/64 = seg 2 A
segundo A = 17/8
Sabemos, cos 2 A = 1/seg 2 A
cos 2 A = 64/289
sen 2 A = 1 – cos2A
sen 2 A = 225/289
sen A = 15/17
Pregunta 5: Dado sec θ = 13/12, calcule todas las demás razones trigonométricas.
Solución.
Usando el teorema de Pitágoras,
sen θ = 5/13
cos θ = 12/13
tan θ = 5/12
cosec θ = 13/5
cuna θ = 12/5
Pregunta 6: Si ∠A y ∠B son ángulos agudos tales que cos A = cos B, entonces demuestra que ∠A = ∠B.
Solución:
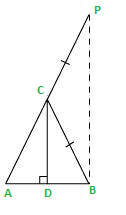
Consideremos un ΔABC en el que CD ⊥ AB.
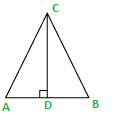
Se da que cos A = cos B
AD/AC = BD/BC … (1)
Necesitamos probar ∠A = ∠B. Para probar esto, necesitamos extender AC a P tal que BC = CP.
De la ecuación (1), obtenemos
AD/BD = AC/BC
AD/BD = AC/CP (BC = CP por construcción)
Usando el inverso de BPT (Teorema de proporcionalidad básica),
CD||BP
∠ACD = ∠CPB (Ángulos correspondientes) … (3)
Y, ∠BCD = ∠CBP (Ángulos interiores alternos) … (4)
Por construcción, tenemos BC = CP.
∴ ∠CBP = ∠CPB (Ángulo opuesto a lados iguales de un triángulo) … (5)
De las ecuaciones (3), (4) y (5), obtenemos
∠ACD = ∠BCD … (6)
En ΔCAD y ΔCBD,
∠ACD = ∠BCD (Usando la ecuación (6))
∠CDA = ∠CDB (Ambos 90°)
Por lo tanto, los ángulos restantes deben ser iguales.
∴∠CAD = ∠CDB
⇒ ∠A = ∠B
Pregunta 7: Si cot θ = 7/8, evalúa
(i) ((1 + sen θ) * (1 – senθ))/(1 + cosθ) * (1 – cosθ )))
(ii) cuna 2 θ
Solución:
(i) Usando (a + b) * (a – b) = a 2 – b 2 en numerador y denominador
Obtenemos
(1 – sen 2 θ)/(1 – cos 2 θ)
Usando sen 2 θ + cos 2 θ = 1
Obtenemos
cos 2 θ/sen 2 θ = cot 2 θ
Ahora
cuna 2 θ = (7/8)2 = 49/64
(ii) cuna 2 θ = (7/8)2 = 49/64
Pregunta 8. Si 3 cot A = 4, comprueba si (1 – tan 2 A)/(1 + tan 2 A) = cos 2 A – sen 2 A
Solución.
Sabemos que, tanA = sinA / cosA ….(1)
Usando (1) en LHS
= (1 – sen 2 A/cos 2 A)/(1 + sen 2 A/cos 2 A)
que al reorganizar se convierte en
= (cos 2 A – sen 2 A)/(cos 2 A + sen 2 A)
Usando la identidad,
cos 2 A + sen 2 A = 1
LHS se convierte en
= (cos 2 A – sen 2 A)
Esto es igual a RHS.
LHS = RHS (para cada valor de cot A)
Por lo tanto, Probado.
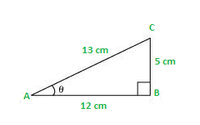
Pregunta 9: En Δ ABC, en ángulo recto en B. Si tan A = 1/(3 1/2 ), encuentre el valor de
(i) sen A cos C+ cos A sen C
(ii) cos A cos C − sen A sen C
Solución:
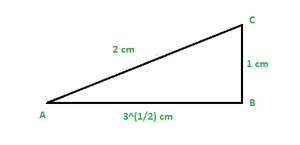
Usando el teorema de Pitágoras
(AB) 2 + (BC) 2 = (AC) 2
(31/2) 2 + (1) 2 = (CA) 2
lo que da
CA = 2 cm
Usando fórmulas
sen A = 1/2
sen C = 3 1/2 /2
porque A = 3 1/2 /2
porque C = 1/2
Ahora, (i) sen A cos C+ cos A sen C
Sustituyendo los valores
= (1/2) * (1/2) + (3 1/2 /2) * (3 1/2 /2)
= 1/4 + 3/4
= 1
Ahora, (ii) cos A cos C − sen A sen C
Sustituyendo los valores
= (3 1/2 /2) * (1/2) – (1/2) * (3 1/2 /2)
= 3 1/2 /4 – 3 1/2 /4
= 0
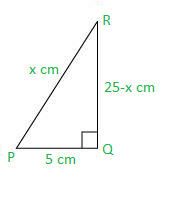
Pregunta 10: En Δ PQR, rectángulo en Q, PR + QR = 25 cm y PQ = 5 cm. Determine los valores de sen P, cos P y tan P.
Solución:
Dado que, PR + QR = 25
PQ = 5
Sea PR x cm.
Por lo tanto, QR = 25 − x cm
Aplicando el teorema de Pitágoras en ΔPQR, obtenemos
PR 2 = PQ 2 + QR 2
x 2 = (5) 2 + (25 − x) 2
x2 = 25 + 625 + x2 − 50x
50x = 650
x = 13
Por lo tanto, PR = 13 cm
QR = (25 − 13) cm = 12 cm
Ahora,
sen P = QR/PR = 12/13
porque P = PQ/PR = 5/13
tan P = QR/PQ = 12/5
Pregunta 11. Indique si las siguientes son verdaderas o falsas. Justifica tu respuesta.
(i) El valor de tan P siempre es menor que 1.
(ii) sec A = 12/5 para algún valor del ángulo A.
(iii) cos A es la abreviatura utilizada para la cosecante del ángulo A.
(iv) cot A es el producto de cot y A
(v) sen θ = 4/3, para algún ángulo θ
Solución:
(i) Considere un ΔPQR, en ángulo recto en Q como se muestra a continuación.
Aquí tan P = 12/5 que seguramente es mayor que 1.
Por lo tanto, la afirmación es falsa.
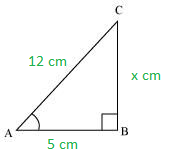
(ii) Considere ΔABC con AB = 5 cm, AC = 12 cm y BC = x cm
Usando el teorema de Pitágoras en ΔABC
(AB) 2 + (BC)2 = (AC)2
52 + x2 = 122
x = (144 – 25)1/2
x = (119)1/2
x = 10,9 cm
AB < BC < CA
Así que este triángulo es válido,
Por lo tanto, la afirmación dada es verdadera.
(iii) La abreviatura utilizada para la cosecante A es cosec A. Y cos A es la abreviatura utilizada para el coseno A.
Por lo tanto, la afirmación dada es falsa.
(iv) cot A no es el producto de cot y A. Es la cotangente de ∠A.
Por lo tanto, la afirmación dada es falsa.
(v) sen θ = 4/3
En un triángulo rectángulo, la hipotenusa siempre es mayor que los dos lados restantes. Por lo tanto, tal valor de sen θ no es posible.
Por lo tanto, la afirmación dada es falsa.
Publicación traducida automáticamente
Artículo escrito por TarunYadav4 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA