Clase 10 Soluciones NCERT – Capítulo 4 Ecuaciones cuadráticas – Ejercicio 4.3

Pregunta 1. Encuentra las raíces de las siguientes ecuaciones cuadráticas, si existen, por el método de completar el cuadrado:

(yo) 2x ² – 7x + 3 = 0

Solución:

2x ² – 7x = – 3

Dividiendo por 2 en ambos lados, obtenemos

x ² – $\frac{7x}{2}$ = – $\frac{3}{2}$

x ² -2 × x × $\frac{7}{4}$ = – $\frac{3}{2}$

Al sumar ( $\frac{7}{4}$ ) ² a ambos lados de la ecuación, obtenemos

(x) ² – 2×x× $\frac{7}{4}$ +( $\frac{7}{4}$ ) ² = ( $\frac{7}{4}$ ) ² – $\frac{3}{2}$

(x- $\frac{7}{4}$ ) ² = ( $\frac{49}{16}$ ) – ( $\frac{3}{2}$ ) (Usando la identidad: a ² – 2ab + b ² = (ab) ² )

(x- $\frac{7}{4}$ ) ² = $\frac{25}{16}$

(x- $\frac{7}{4}$ ) ² = ± $\frac{5}{4}$

x = $\frac{7}{4} &pm; \frac{5}{4}$

x = $\frac{7}{4} + \frac{5}{4}$ o x = $\frac{7}{4} - \frac{5}{4}$

x = $\frac{12}{4}$ o x = $\frac{2}{4}$

x = 3 o x = $\frac{1}{2}$

(ii) 2x ² + x – 4 = 0

Solución:

2x ² + x = 4

Dividiendo ambos lados de la ecuación por 2, obtenemos

x ² + $\frac{x}{2}$ = 2

Ahora, al sumar $(\frac{1}{4})$ ² a ambos lados de la ecuación, obtenemos,

(x) ² + 2 × x × $\frac{1}{4}$ + ( $\frac{1}{4}$ ) ² = 2 + ( $\frac{1}{4}$ ) ²

(x + $\frac{1}{4}$ )2 = $\frac{33}{16}$ (Usando la identidad: a ² + 2ab + b ² = (a+b) ² )

x + $\frac{1}{4}$ = ± $√(\frac{33}{16})$

x = $- \frac{1}{4} &pm; \frac{√33}{4}$

x = $\frac{-1&pm; √33}{4}$

Por lo tanto, x = $\frac{-1+ √33}{4}$ o x = $\frac{-1- √33}{4}$

(iii) 4x ² + 4√3x + 3 = 0

Solución:

4×2 + 4√3x ⁼ -3

Dividiendo ambos lados de la ecuación por 4, obtenemos

x2 ⁺ √3x = – $\frac{3}{4}$

Ahora, al sumar ( $\frac{√3}{2}$ ) ² a ambos lados de la ecuación, obtenemos,

(x) ² + 2 × x × $\frac{√3}{2}$ + ( $\frac{√3}{2}$ ) ² = – $\frac{3}{4}$ + ( $\frac{√3}{2}$ ) ²

(x + $\frac{√3}{2}$ ) ² = 0 (Usando la identidad: a ² + 2ab + b ² = (a+b) ² )

Por lo tanto, x = – $\frac{√3}{2}$ o x = – $\frac{√3}{2}$

(iv) 2x ² + x + 4 = 0

Solución:

2x ² + x = -4

Dividiendo ambos lados de la ecuación por 2, obtenemos

x ² + $\frac{x}{2}$ = -2

Ahora, al sumar ( $\frac{1}{4}$ ) ² a ambos lados de la ecuación, obtenemos,

(x) ² + 2 × x × $\frac{1}{4}$ + ( $\frac{1}{4}$ ) ² = – 2 + ( $\frac{1}{4}$ ) ²

(x + $\frac{1}{4}$ ) ² = $\frac{-31}{16}$ (Usando la identidad: a ² + 2ab + b ² = (a+b) ² )

Como sabemos, el cuadrado de los números no puede ser negativo.

Por lo tanto, no existe una raíz real para la ecuación dada, 2x ² + x + 4 = 0.

Pregunta 2. Encuentra las raíces de las ecuaciones cuadráticas dadas en P.1 anterior aplicando la fórmula cuadrática.

(yo) 2x ² – 7x + 3 = 0

Solución:

Al comparar la ecuación con ax ² + bx + c = 0, obtenemos,

a = 2, b = -7 y c = 3

Entonces raíces de la ecuación cuadrática = $\frac{-b&pm; √(b^2-4ac)}{2a}$

x = $\frac{-(-7)&pm; √((-7)^2-4(2)(3))}{2(2)}$

x = $\frac{7&pm; √(49-24)}{4}$

x = $\frac{7&pm; √25}{4}$

x = $\frac{7&pm; 5}{4}$

x = $\frac{7+5}{4}$ o x = $\frac{7-5}{4}$

x = $\frac{12}{4}$ o $\frac{2}{4}$

x = 3 o $\frac{1}{2}$

(ii) 2x ² + x – 4 = 0

Solución:

Al comparar la ecuación con ax ² + bx + c = 0, obtenemos,

a = 2, b = 1 y c = -4

Entonces raíces de la ecuación cuadrática = $\frac{-b&pm; √(b^2-4ac)}{2a}$

x = $\frac{-1&pm; √(1^2-4(2)(-4))}{2(2)}$

x = $\frac{-1&pm; √(1+32)}{4}$

x = $\frac{-1&pm; √33}{4}$

x = $\frac{-1+√33}{4}$ o x = $\frac{1-√33}{4}$

(iii) 4x ² + 4√3x + 3 = 0

Solución:

Al comparar la ecuación con ax ² + bx + c = 0, obtenemos,

a = 4, b = 4√3 y c = 3

Entonces raíces de la ecuación cuadrática = $\frac{-b&pm; √(b^2-4ac)}{2a}$

x = $\frac{-(4√3)&pm; √((4√3)^2-4(4)(3))}{2(4)}$

x = $\frac{-(4√3)&pm; √(48-48)}{8}$

x = $\frac{-4√3}{8}$

x = $\frac{-√3}{2}$ o x = $\frac{-√3}{2}$

(iv) 2x ² + x + 4 = 0

Solución:

Al comparar la ecuación con ax ² + bx + c = 0, obtenemos,

a = 2, b = 1 y c = 4

Entonces raíces de la ecuación cuadrática = $\frac{-b&pm; √(b^2-4ac)}{2a}$

x = $\frac{-1&pm; √(1^2-4(2)(4))}{2(2)}$

x = $\frac{-1&pm; √(1-32)}{4}$

x = $\frac{-1&pm; √(-31)}{4}$

Como sabemos, el cuadrado de un número nunca puede ser negativo.

Por lo tanto, no hay una solución real para la ecuación dada.

Pregunta 3. Encuentra las raíces de las siguientes ecuaciones:

(i) x – $\frac{1}{x}$ = 3, x ≠ 0

Solución:

Después de reorganizar, obtenemos

x ² – 3x -1 = 0

Al comparar la ecuación con ax ² + bx + c = 0, obtenemos,

a = 1, b = -3 y c = -1

Entonces raíces de la ecuación cuadrática = $\frac{-b&pm; √(b^2-4ac)}{2a}$

x = $\frac{-(-3)&pm; √((-3)^2-4(1)(-1))}{2(1)}$

x = $\frac{3&pm; √(9+4)}{2}$

x = $\frac{3&pm;√(13)}{2}$

x = $\frac{3+√(13)}{2}$ o x = $\frac{3-√(13)}{2}$

(ii) $\frac{1}{x+4} - \frac{1}{x-7} = \frac{11}{30}$ , x ≠ -4,7

Solución:

$\frac{(x-7-x-4)}{(x+4)(x-7)} = \frac{11}{30}$

$\frac{(-11)}{(x+4)(x-7)} = \frac{11}{30}$

Después de reorganizar,

(x+4)(x-7) = -30

x ² – 3x – 28 = 30

x ² – 3x + 2 = 0

Al comparar la ecuación con ax ² + bx + c = 0, obtenemos,

a = 1, b = -3 y c = 2

Entonces raíces de la ecuación cuadrática = $\frac{-b&pm; √(b^2-4ac)}{2a}$

x = $\frac{-(-3)&pm; √((-3)^2-4(1)(2))}{2(1)}$

x = $\frac{3&pm; √(9-8)}{2}$

x = $\frac{3&pm;√1}{2}$

x = $\frac{3&pm;1}{2}$

x = $\frac{4}{2}$ o x = $\frac{2}{2}$

x = 2 o x = 1

Pregunta 4. La suma de los recíprocos de las edades de Rehman, (en años) hace 3 años y dentro de 5 años es 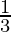$\frac{1}{3}$ . Halla su edad actual.

Solución:

Echemos,

La edad actual de Rehman es x años.

Hace tres años, la edad de Rehman era (x – 3) años.

Cinco años después, su edad será (x + 5) años.

Según la condición dada,

$\frac{1}{x-3} + \frac{1}{x-5} = \frac{1}{3}$

$\frac{(x+5+x-3)}{(x-3)(x+5)} = \frac{1}{3}$

$\frac{(2x+2)}{(x-3)(x+5)} = \frac{1}{3}$

3(2x + 2) = (x-3)(x+5)

6x + 6 = x2 + ^2x – 15

x ² – 4x – 21 = 0

x ² – 7x + 3x – 21 = 0 (factorizando)

x(x-7) + 3(x-7) = 0

(x – 7)(x + 3) = 0

x = 7, -3

Como, la edad no puede ser negativa.

Por lo tanto, la edad actual de Rehman es de 7 años.

Pregunta 5. En una prueba de clase, la suma de las calificaciones de Shefali en Matemáticas e Inglés es 30. Si hubiera obtenido 2 puntos más en Matemáticas y 3 puntos menos en Inglés, el producto de sus puntos habría sido 210. Encuentra sus puntos en el dos sujetos

Solución:

Echemos,

Las marcas de Shefali en Matemáticas son x.

Entonces, las marcas en inglés serán 30 – x.

Según la condición dada,

(x + 2)(30 – x – 3) = 210

(x + 2)(27 – x) = 210

-x ² + 25x + 54 = 210

Multiplica la ecuación por (-1),

x ² – 25x + 156 = 0

x ² – 12x – 13x + 156 = 0

x(x-12) -13(x-12) = 0

(x-12)(x-13) = 0

x = 12, 13

Por lo tanto, si las calificaciones en Matemáticas son 12, entonces las calificaciones en Inglés serán 30 – 12 = 18

y las notas en Matemáticas son 13, entonces las notas en Inglés serán 30 – 13 = 17.

Pregunta 6. La diagonal de un campo rectangular mide 60 metros más que el lado más corto. Si el lado más largo mide 30 metros más que el lado más corto, halla los lados del campo.

Solución:

Echemos,

ancho = x

Longitud = x+30

Diagonal = x+60

Diagonal = √(Largo ² + Ancho ² )

Según la condición dada,

√((x+30) ² + (x) ² ) = x+60

Cuadrando ambos lados,

x ² + (x + 30) ² = (x + 60) ²

x2 ⁺ x2 ⁺ 900 + 60x = x2 ⁺ 3600 + 120x

x ² – 60x – 2700 = 0

x ² – 90x + 30x – 2700 = 0

x(x-90) + 30(x-90) = 0

(x – 90)(x + 30) = 0

x = 90, -30

Como, el lado del campo no puede ser negativo.

Por lo tanto, la longitud del lado más corto será de 90 m.

y, la longitud del lado mayor será (90 + 30) m = 120 m.

Pregunta 7. La diferencia de cuadrados de dos números es 180. El cuadrado del número menor es 8 veces el número mayor. Encuentra los dos números.

Solución:

Echemos,

El número mayor = x

y, número menor = y

Según la condición dada,

x ² – y ² = 180 y y ² = 8x (Significa que x tiene que ser positivo, porque se obtiene elevando un número al cuadrado)

x2 – 8x = ¹⁸⁰

x ² – 8x – 180 = 0

x ² – 18x + 10x – 180 = 0

x(x-18) +10(x-18) = 0

(x – 18)(x + 10) = 0

x = 18, -10

Como x no puede ser negativo,

Por lo tanto, el número mayor será 18.

X = 18

Entonces, como y ² = 8x

= 8 × 18

= 144

y = ±√144 = ±12

Entonces, número más pequeño = ±12

Por lo tanto, los números son 18 y 12 o 18 y -12.

Pregunta 8. Un tren recorre 360 km a una velocidad uniforme. Si la velocidad hubiera sido 5 km/h más, habría tardado 1 hora menos en el mismo recorrido. Encuentre la velocidad del tren.

Solución:

Echemos

La velocidad del tren = x km/h.

Como, Velocidad = $\frac{Distance}{Time}$

Tiempo necesario para recorrer 360 km = $\frac{360}{x}$ hr.

Según la pregunta dada,

(x + 5)( $\frac{360}{x}$ -1) = 360

(x + 5)( $\frac{360 - x}{x}$ ) = 360

(x + 5)(360 – x) = 360x

x2 ⁺ 5x -1800 = 0

x2 ⁺ 45x – 40x + 1800 = 0

x(x+45) -40(x+45) = 0

(x + 45)(x – 40) = 0

x = 40, -45

Como sabemos, el valor de la velocidad no puede ser negativo.

Por lo tanto, la velocidad del tren es de 40 km/h.

Pregunta 9. Dos grifos de agua juntos pueden llenar un tanque en 9 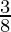$\frac{3}{8}$ horas. El grifo de mayor diámetro tarda 10 horas menos que el más pequeño en llenar el depósito por separado. Encuentre el tiempo en el que cada grifo puede llenar el tanque por separado.

Solución:

Echemos

El tiempo que tarda la tubería más pequeña en llenar el tanque = x hr.

Tiempo que tarda la tubería más grande = (x – 10) hr

Parte del tanque lleno por tubería más pequeña en 1 hora = $\frac{1}{x}$

Parte del tanque lleno por tubería más grande en 1 hora = $\frac{1}{x-10}$

Según la condición dada,

Se tardaron 9 $\frac{3}{8}$ horas en llenar tanto la tubería.

Asi que,

$\frac{1}{x} + \frac{1}{x-10} = \frac{8}{75}$

$\frac{x-10+x}{x(x-10)} = \frac{8}{75}$

$\frac{2x-10}{x(x-10)} = \frac{8}{75}$

75(2x – 10) = 8x ² – 80x

150x – 750 = 8x ² – 80x

8x ² – 230x +750 = 0

8x ² – 200x – 30x + 750 = 0

8x(x-25) -30(x-25) = 0

(x – 25)(8x -30) = 0

x = 25, $\frac{30}{8}$

El tiempo que tarda la tubería más pequeña no puede ser $\frac{30}{8}$ horas, ya que el tiempo que tarda la tubería más grande se vuelve negativo.

Por lo tanto, el tiempo que tarda la tubería más pequeña = 25 horas

y, por la tubería mayor = 15 horas

Pregunta 10. Un tren expreso tarda 1 hora menos que un tren de pasajeros en recorrer 132 km entre Mysore y Bangalore (sin tener en cuenta el tiempo que se detienen en las estaciones intermedias). Si la velocidad promedio del tren expreso es 11 km/h más que la del tren de pasajeros, encuentre la velocidad promedio de los dos trenes.

Solución:

Echemos

La velocidad media del tren de pasajeros = x km/h.

Velocidad media del tren expreso = (x + 11) km/h

Según la condición dada,

$\frac{132}{x} + \frac{132}{x+11}$ = 1

$\frac{132(x+11-x)}{x(x+11)}$ = 1

$\frac{132 × 11}{x(x+11)}$ = 1

132 × 11 = x(x + 11)

x2 ⁺ 11x – 1452 = 0

x2 ⁺ 44x -33x -1452 = 0

x(x + 44) -33(x + 44) = 0

(x + 44)(x – 33) = 0

x = – 44, 33

Como sabemos, la Velocidad no puede ser negativa.

Por lo tanto, la velocidad del tren de pasajeros será de 33 km/h.

y, la velocidad del tren expreso será 33 + 11 = 44 km/h.

Pregunta 11. La suma de las áreas de dos cuadrados es 468 m ² . Si la diferencia de sus perímetros es de 24 m, halla los lados de los dos cuadrados.

Solución:

Sean los lados de los dos cuadrados x e y metros.

Perímetro = 4x y 4y respectivamente

Área = x ² y y ² respectivamente.

Según la condición dada,

4x – 4y = 24

x – y = 6

x = y + 6 ………………….(I)

y,

x2 + ^y2⁼ 468

(6 + y) ² + y ² = 468 (De (I))

36 + ^y2 + 12y + y2 ⁼ 468

2 años ² + 12 años + 432 = 0

y ² + 6y – 216 = 0

y ² + 18y – 12y – 216 = 0

y(y+18) -12(y+18) = 0

(y + 18)(y – 12) = 0

y = -18, 12

Como sabemos, el lado de un cuadrado no puede ser negativo.

Por lo tanto, los lados de los cuadrados miden 12 m.

y, (12 + 6) m = 18 m .

Publicación traducida automáticamente

Artículo escrito por adi1212 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra las raíces de las siguientes ecuaciones cuadráticas, si existen, por el método de completar el cuadrado:

(yo) 2x 2 – 7x + 3 = 0

(ii) 2x 2 + x – 4 = 0

(iii) 4x 2 + 4√3x + 3 = 0

(iv) 2x 2 + x + 4 = 0

Pregunta 2. Encuentra las raíces de las ecuaciones cuadráticas dadas en P.1 anterior aplicando la fórmula cuadrática.

(yo) 2x 2 – 7x + 3 = 0

(ii) 2x 2 + x – 4 = 0

(iii) 4x 2 + 4√3x + 3 = 0

(iv) 2x 2 + x + 4 = 0

Pregunta 3. Encuentra las raíces de las siguientes ecuaciones:

(i) x – = 3, x ≠ 0

(ii) , x ≠ -4,7

Pregunta 4. La suma de los recíprocos de las edades de Rehman, (en años) hace 3 años y dentro de 5 años es . Halla su edad actual.

Pregunta 5. En una prueba de clase, la suma de las calificaciones de Shefali en Matemáticas e Inglés es 30. Si hubiera obtenido 2 puntos más en Matemáticas y 3 puntos menos en Inglés, el producto de sus puntos habría sido 210. Encuentra sus puntos en el dos sujetos

Pregunta 6. La diagonal de un campo rectangular mide 60 metros más que el lado más corto. Si el lado más largo mide 30 metros más que el lado más corto, halla los lados del campo.

Pregunta 7. La diferencia de cuadrados de dos números es 180. El cuadrado del número menor es 8 veces el número mayor. Encuentra los dos números.

Pregunta 8. Un tren recorre 360 ​​km a una velocidad uniforme. Si la velocidad hubiera sido 5 km/h más, habría tardado 1 hora menos en el mismo recorrido. Encuentre la velocidad del tren.

Pregunta 9. Dos grifos de agua juntos pueden llenar un tanque en 9 horas. El grifo de mayor diámetro tarda 10 horas menos que el más pequeño en llenar el depósito por separado. Encuentre el tiempo en el que cada grifo puede llenar el tanque por separado.

Pregunta 11. La suma de las áreas de dos cuadrados es 468 m 2 . Si la diferencia de sus perímetros es de 24 m, halla los lados de los dos cuadrados.

Deja una respuesta Cancelar la respuesta

(yo) 2x ² – 7x + 3 = 0

(ii) 2x ² + x – 4 = 0

(iii) 4x ² + 4√3x + 3 = 0

(iv) 2x ² + x + 4 = 0

(yo) 2x ² – 7x + 3 = 0

(ii) 2x ² + x – 4 = 0

(iii) 4x ² + 4√3x + 3 = 0

(iv) 2x ² + x + 4 = 0

(i) x – $\frac{1}{x}$ = 3, x ≠ 0

(ii) $\frac{1}{x+4} - \frac{1}{x-7} = \frac{11}{30}$ , x ≠ -4,7

Pregunta 4. La suma de los recíprocos de las edades de Rehman, (en años) hace 3 años y dentro de 5 años es $\frac{1}{3}$ . Halla su edad actual.

Pregunta 8. Un tren recorre 360 km a una velocidad uniforme. Si la velocidad hubiera sido 5 km/h más, habría tardado 1 hora menos en el mismo recorrido. Encuentre la velocidad del tren.

Pregunta 9. Dos grifos de agua juntos pueden llenar un tanque en 9 $\frac{3}{8}$ horas. El grifo de mayor diámetro tarda 10 horas menos que el más pequeño en llenar el depósito por separado. Encuentre el tiempo en el que cada grifo puede llenar el tanque por separado.

Pregunta 11. La suma de las áreas de dos cuadrados es 468 m ² . Si la diferencia de sus perímetros es de 24 m, halla los lados de los dos cuadrados.