Capítulo 6 Triángulos – Ejercicio 6.5 | conjunto 1
Pregunta 11. Un avión sale de un aeropuerto y vuela hacia el norte a una velocidad de 1000 km por hora. Al mismo tiempo, otro avión sale del mismo aeropuerto y vuela hacia el oeste a una velocidad de 1200 km por hora. ¿A qué distancia estarán los dos aviones después de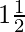 
horas?
Solución:
Distancia recorrida por plaza izquierda hacia el norte = 1000 * 1,5
Distancia recorrida por lugar dejado hacia el oeste = 1200 * 1.5 = 1800km
En la derecha ∆ABC por el teorema de Pitágoras
(AC) 2 = (AB) 2 + (BC) 2
(CA) 2 = (1500) 2 + (1800) 2
= 250000 + 3240000
= 5490000
= √(3 * 3 * 61 * 10 * 10 * 10 * 10)
= 3 * 10 * 10√61
CA = 300√61
Distancia entre los dos polos 300√61km
Pregunta 12. Dos postes de 6 my 11 m de altura se encuentran sobre un suelo plano. Si la distancia entre los pies de los postes es de 12 m, encuentre la distancia entre sus puntas.
Solución:
AB es poste de altura = 11m
DC es otro poste de altura = 6m
BC = 12m
En la Fig. DE = BC = 12m
AE = AB-EB
= 11 – 6
= 5m
En derecha ∆AED, por el teorema de Pitágoras
(AD) 2 = (AC) 2 + (DE) 2
(AD) 2 = (5) 2 + (12) 2
(AD) 2 = 25 + 144
DA = √169
DA = √(13 * 13)
DA = 13
Por lo tanto, la distancia entre las puntas de los dos postes es de 13 m.
Pregunta 13. D y E son puntos en los lados CA y CB respectivamente de un triángulo ABC en ángulo recto en C. Demuestre que AE 2 + BD 2 = AB 2 + DE 2 .
Solución:
Para probar: (AE) 2 + (BD) 2 = (AB) 2 + (DE) 2
Construcción: Une AE, BD y DE
Prueba:
En ∆ACE, por el teorema de Pitágoras
(AE) 2 = (CA) 2 + (CE) 2 -(1)
En ∆DCB, por el teorema de Pitágoras
(BD) 2 = (DC) 2 + (BC) 2 -(2)
En ∆ACB, por el teorema de Pitágoras
(AB) 2 = (AC) 2 + (CB) 2 -(3)
En ∆DCE, por el teorema de Pitágoras
(ED) 2 = (DC) 2 + (CE) 2
Sumando las ecuaciones (1) y (2)
(AE) 2 + (BD) 2 = (CA) 2 + (EC) 2 + (CC) 2 + (CC) 2
= (AC 2 + BC 2 ) + (EC 2 + DC 2 )
= AB 2 + DE 2 -(de 3 y 4)
Pregunta 14. La perpendicular desde A en el lado BC de un Δ ABC interseca a BC en D tal que DB = 3CD (ver Fig.). Demuestre que 2AB 2 = 2AC 2 + BC 2 .
Solución:
Dado: DB = 3CD
Para probar: 2AB 2 = 2AC 2 + BC 2
Prueba: DB = 3CD
BC = CD + DB
BC = CD + 3CD
BC = 4 CD
BC/4 = CD -(1)
DB = 3(BC/4) -(2)
En la derecha ∆ADB, por el teorema de Pitágoras
AB 2 = AD 2 + DB 2 -(3)
En derecho ∆ADC, por el teorema de Pitágoras
AC 2 = AD 2 + CD 2 -(4)
Reste la ecuación (3) de (4)
AB 2 – AC 2 = AD 2 + DB 2 – (AD 2 + CD 2 )
= AD 2 + DB 2 + AD 2 – CD 2
= BD 2 – CD 2
= (3/4BC) 2 – (BC/4) 2
= 9/6BC 2 – BC/16
= 8BC 2/16
= AB 2 – AC 2 = BC 2 /2
2AB2 – 2AC2 = BC2 _
2AB2 = 2AC2 + BC2 _
Pregunta 15. En un triángulo equilátero ABC, D es un punto del lado BC tal que BD = 1/3BC. Demuestre que 9AD 2 = 7AB 2 .
Solución:
Demostrar que 9AD 2 = 7AB 2
Construcción: Unir AD y trazar AE perpendicular BC
Sea cada lado, AB = AC = BC = a
BD = 1/3BC = 1/3a
BC = 1/2BC = 1/2a
DE = SER – BD
= 1/2a – 1/3a
= 3a – 2a/6
= DE = a/6
En derecha ∆AED, por el teorema de Pitágoras
AD 2 = AE 2 + DE 2
DA 2 = (√3a/2) 2 + (a/6) 2
= 3a 2 /4+ a 2 /36
= 27a 2 /36 + a 2 /36
2 d.C. = 28a 2/36
AD 2 = 7a 2 /9
9AD 2 = 7a 2
9AD 2 = 7AB 2
Pregunta 16. En un triángulo equilátero, demostrar que tres veces el cuadrado de un lado es igual a cuatro veces el cuadrado de una de sus alturas.
Solución:
Para probar: 3AB 2 = 4AD 2
Demostración: Sea cada lado de un equilátero ∆ = a
BD = 1/2a -[perpendicular biseca el lado en un equilátero ∆]
En la derecha ∆ADB, por el teorema de Pitágoras
(AB) 2 = (AD) 2 + (BD) 2
(a) 2 = (AD) 2 + (1/2a) 2
a 2 = AD 2 + (a/2) 2
a 2 – a 2 /4 = AD 2
3a 2 /4 = AD 2
3a 2 = 4AD 2
3AB 2 = 4AD 2
Pregunta 17. Marca la respuesta correcta y justifica: En ΔABC, AB = 6√3 cm, AC = 12 cm y BC = 6 cm. El ángulo B es:
(A) 120° (B) 60°
(C) 90° (D) 45°
Solución:
(CA) 2 = (12) 2 = 144
(AB) 2 = (6√3) 2 = 6 * 6√3 = 36 * 3 = 108
(BC) 2 = (6) 2 = 36
(AB) 2 + (BC) 2 = 108 + 36 = 144
∴ Es correcto ∆ entonces ∠B = 90°
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA