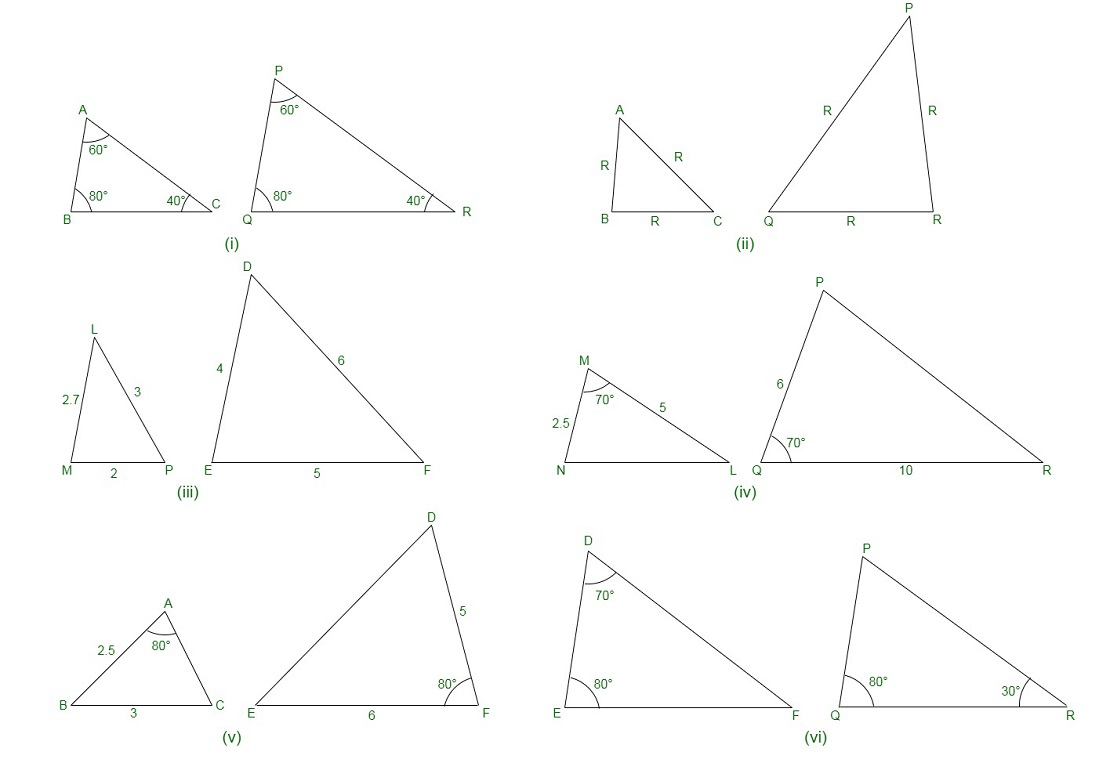
Pregunta 1. Indique qué pares de triángulos en la figura son similares. Escribe el criterio de similitud que usaste para responder la pregunta y también escribe los pares de triángulos similares en la forma simbólica:
Solución:
(i) Tenemos, en ΔABC y ΔPQR,
∠A = ∠P = 60°
∠B = ∠Q = 80°
∠C = ∠R = 40°
Por el criterio de similitud AAA, tenemos
∴ ΔABC ~ ΔPQR
(ii) Tenemos, en ΔABC y ΔPQR,
Calculando las razones de los lados correspondientes,
AB/QR = 2,5/5 = 1/2
BC/PR = 2/4 = 1/2
CA/PQ = 3/6 = 1/2
AB/QR = BC/RP = CA/PQ
Ahora,
Por el criterio de similitud SSS, tenemos
ΔABC ~ ΔQRP
(iii) Tenemos, en ΔLMP y ΔDEF,
Ahora,
LM = 2,7, MP = 2, LP = 3, EF = 5, DE = 4, DF = 6
Calculando las razones de los lados correspondientes,
MP/DE = 2/4 = 1/2
PL/DF = 3/6 = 1/2
LM/EF = 2,7/5 = 27/50
Ya que, MP/DE = PL/DF ≠ LM/EF
Por lo tanto, ΔLMP y ΔDEF no son similares.
(iv) En ΔMNL y ΔQPR, se da,
Calculando las razones de los lados correspondientes,
MN/QP = ML/QR = 1/2
Y,
∠M = ∠Q = 70°
Por criterio de similitud SAS
ΔMNL ~ ΔQPR
(v) En ΔABC y ΔDEF, tenemos,
AB = 2,5, BC = 3, ∠A = 80°, EF = 6, DF = 5, ∠F = 80°
Calculando las razones de los lados correspondientes,
AB/DF = 2,5/5 = 1/2
Y, BC/EF = 3/6 = 1/2
⇒ ∠B ≠ ∠F
Por lo tanto, ΔABC y ΔDEF no son similares.
(vi) En ΔDEF,
Por la propiedad de la suma de los ángulos de un triángulo,
∠D + ∠E + ∠F = 180°
⇒ 70° + 80° + ∠F = 180°
⇒ ∠F = 180° – 70° – 80°
⇒ ∠F = 30°
De manera similar, en ΔPQR,
Por la propiedad de la suma de los ángulos de un triángulo,
∠P + ∠Q + ∠R = 180
⇒ ∠P + 80° + 30° = 180°
⇒ ∠P = 180° – 80° -30°
⇒ ∠P = 70°
Ahora, en ΔDEF y ΔPQR, tenemos
∠D = ∠P = 70° [ángulos correspondientes iguales]
∠F = ∠Q = 80°
∠F = ∠R = 30°
Por lo tanto,
Por criterio de similitud AAA,
ΔDEF ~ ΔPQR
Pregunta 2. En la figura, ΔODC ∝ ¼ ΔOBA, ∠ BOC = 125° y ∠ CDO = 70°. Encuentre ∠ DOC, ∠ DCO y ∠ OAB.
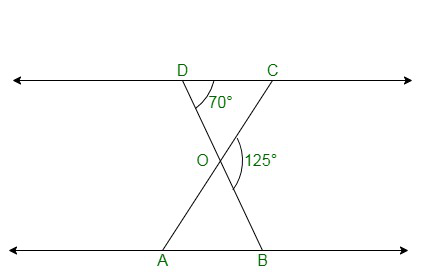
Solución:
Sabemos, DOB es una línea recta, como se da.
Por lo tanto, ∠DOC+ ∠COB = 180°
También,
∠BOC = 125°
⇒ ∠DOC = 180° – 125°
= 55°
En ΔDOC
Por la propiedad de la suma de los ángulos de un triángulo,
∠DCO + ∠CDO + ∠DOC = 180°
∠CDO = 70°
⇒ ∠DCO + 70º + 55º = 180°
⇒ ∠DCO = 55°
Asimismo, dado,
ΔODC ∝ ¼ ΔOBA,
Por lo tanto, ΔODC ~ ΔOBA.
Como sabemos que los ángulos correspondientes son iguales en triángulos semejantes,
Por lo tanto, ∠OAB = ∠OCD
⇒ ∠ VHA = 55°
∠OAB = ∠OCD
∠OAB = 55°
Pregunta 3. Diagonales AC y BD de un trapecio ABCD con AB || DC se intersecan en el punto O. Utilizando un criterio de semejanza para dos triángulos, demuestre que AO/OC = OB/OD
Solución:
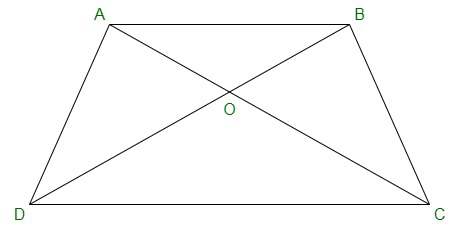
En ΔDOC y ΔBOA,
Dado que, AB || CD, por lo tanto los ángulos alternos interiores son iguales,
Es decir, ∠CDO = ∠ABO ….(i)
Y,
∠DCO = ∠BAO …(ii)
Además, los ángulos verticalmente opuestos son iguales;
Es decir,∠DOC = ∠BOA…(iii)
Por lo tanto, por el criterio de similitud AAA,
ΔDOC ~ ΔBOA [De la ecuación (i), (ii) y (iii)]
Como los triángulos son semejantes, los lados correspondientes son proporcionales.
DO/BO = OC/OA
⇒OA/OC = OB/OD
Por lo tanto, probado.
Pregunta 4. En la fig., QR/QS = QT/PR y ∠1 = ∠2. Demuestre que ΔPQS ~ ΔTQR.
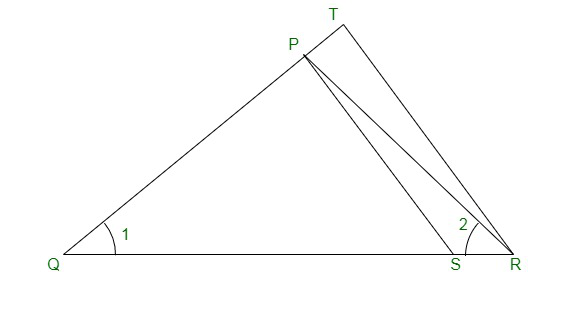
Solución:
Tenemos,
En ΔPQR,
∠PQR = ∠PRQ
Es decir, PQ = PR .…(i)
Dado,
QR/QS = QT/PR
Usando la ecuación (i), obtenemos,
QR/QS = QT/QP …….(ii)
En ΔPQS y ΔTQR,
QR/QS = QT/QP [Usando la ecuación (ii)]
∠Q = ∠Q
Por el criterio de similitud SAS, por lo tanto,
ΔPQS ~ ΔTQR
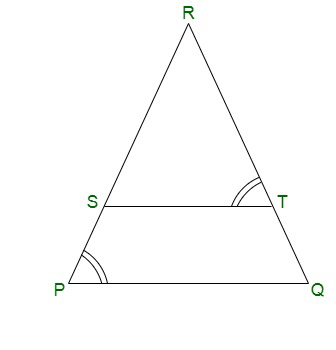
Pregunta 5. S y T son puntos en los lados PR y QR de ΔPQR tales que ∠P = ∠RTS. Demuestre que ΔRPQ ~ ΔRTS.
Solución:
Sabemos,
S y T son los puntos de los lados PR y QR de ΔPQR.
Y, ∠P = ∠RTS.
En ΔRPQ y ΔRTS,
Dado,
∠RTS = ∠QPS
∠R = ∠R (ángulo común)
Por criterio de similitud AAA,
∴ ΔRPQ ~ ΔRTS
Pregunta 6. En la figura, si ΔABE ≅ ΔACD, demuestre que ΔADE ~ ΔABC.
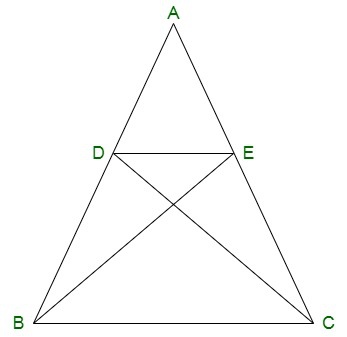
Solución:
Dado, ΔABE ≅ ΔACD.
Por CPCT, tenemos
∴ AB = CA ……….(i)
Y, AD = AE …………(ii)
En ∆ADE y ∆ABC,
Al dividir la ecuación (ii) por la ecuación (i), obtenemos,
AD/AB = AE/AC
Además, por ángulo común,
∠A = ∠A
Por el criterio de similitud SAS, tenemos,
∴ ΔADE ~ ΔABC
Pregunta 7. En la figura, las altitudes AD y CE de ΔABC se intersecan en el punto P. Demuestre que:
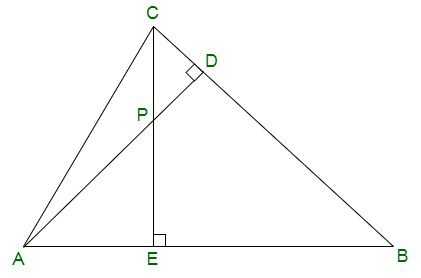
(i) ΔAEP ~ ΔCDP
(ii) ΔABD ~ ΔCBE
(iii) ΔAEP ~ ΔADB
(iv) ΔPDC ~ ΔBEC
Solución:
Dadas, las altitudes AD y CE de ΔABC se intersecan en el punto P.
(i) En ΔAEP y ΔCDP,
Ya que ambos ángulos miden 90° cada uno.
∠AEP = ∠CDP
Ya que,
∠APE = ∠CPD (Ángulos verticalmente opuestos)
Por el criterio de similitud AA, tenemos,
ΔAEP ~ ΔCDP
(ii) En ΔABD y ΔCBE,
Ya que ambos ángulos miden 90° cada uno.
∠ADB = ∠CEB
∠ABD = ∠CBE (ángulos comunes)
Por el criterio de similitud AA, tenemos,
ΔABD ~ ΔCBE
(iii) En ΔAEP y ΔADB,
Ya que ambos ángulos miden 90° cada uno.
∠AEP = ∠ADB
∠PAE = ∠DAB (Ángulos comunes)
Por el criterio de similitud AA, tenemos,
ΔAEP ~ ΔADB
(iv) En ΔPDC y ΔBEC,
Ya que ambos ángulos miden 90° cada uno.
∠PDC = ∠BEC
∠PCD = ∠BCE (ángulos comunes)
Por el criterio de similitud AA, tenemos,
ΔPDC ~ ΔBEC
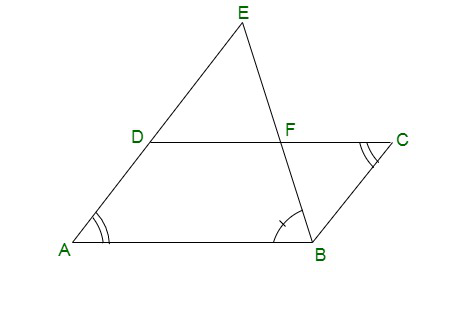
Pregunta 8. E es un punto en el lado AD producido por un paralelogramo ABCD y BE interseca a CD en F. Demuestra que ΔABE ~ ΔCFB.
Solución:
Dado,
E es un punto en el lado AD producido por un paralelogramo ABCD y BE interseca a CD en F.
Ahora,
En ΔABE y ΔCFB,
Como los ángulos opuestos de un paralelogramo son iguales, tenemos,
∠A = ∠C
Además, desde AE || antes de Cristo
∠AEB = ∠CBF (Ángulos interiores alternos)
Por el criterio de similitud AA,
∴ ΔABE ~ ΔCFB
Pregunta 9. En la figura, ABC y AMP son dos triángulos rectángulos, en ángulo recto en B y M respectivamente, prueba que:
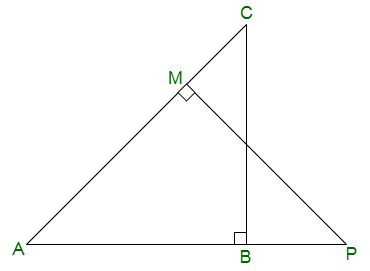
(i) ΔABC ~ ΔAMP
(ii) CA/PA = BC/MP
Solución:
Dado,
ABC y AMP son dos triángulos rectángulos, en ángulo recto en B y M respectivamente.
(i) En ΔABC y ΔAMP, tenemos,
∠CAB = ∠MAP (ángulos comunes)
Ya que ambos ángulos son equivalentes a 90°
∠ABC = ∠AMP
Por el criterio de similitud AA, tenemos,
∴ ΔABC ~ ΔAMP
(ii) Como, ΔABC ~ ΔAMP (criterio de similitud AA) [probado en la parte (i)]
Por lo tanto, sabemos,
Si dos triángulos son semejantes entonces los lados correspondientes son siempre iguales,
Por lo tanto, CA/PA = BC/MP
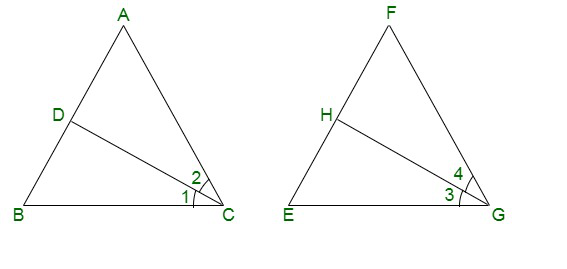
Pregunta 10. CD y GH son respectivamente las bisectrices de ∠ACB y ∠EGF tales que D y H se encuentran en los lados AB y FE de ΔABC y ΔEFG respectivamente. Si ΔABC ~ ΔFEG, demuestre que:
(i) CD/GH = AC/FG
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGF
Solución:
Dado,
CD y GH son respectivamente las bisectrices de ∠ACB y ∠EGF tales que D y H se encuentran en los lados AB y FE de ΔABC y ΔEFG respectivamente.
(yo) Tenemos,
ΔABC ~ ΔFEG.
Por lo tanto,
∠A = ∠F, ∠B = ∠E y ∠ACB = ∠FGE
Ahora, desde,
∠ACB = ∠FGE
∴ ∠ACD = ∠FGH (Bisectriz del ángulo)
Y, ∠DCB = ∠HGE
En ΔACD y ΔFGH,
∠A = ∠F
∠ACD = ∠FGH
Por el criterio de similitud AA, tenemos,
∴ ΔACD ~ ΔFGH
⇒CD/GH = AC/FG
(ii) En ΔDCB y ΔHGE,
Probado en la parte (i)
∠DCB = ∠HGE
∠B = ∠E
Por el criterio de similitud AA,
∴ ΔDCB ~ ΔHGE
(iii) En ΔDCA y ΔHGF,
Como ya hemos probado,
∠ACD = ∠FGH
∠A = ∠F
Por el criterio de similitud AA,
∴ ΔDCA ~ ΔHGF
Publicación traducida automáticamente
Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA