Clase 10 Soluciones NCERT – Capítulo 6 Triángulos – Ejercicio 6.5 | Serie 1

Pregunta 1. Los lados de los triángulos se dan a continuación. Determina cuáles de ellos son triángulos rectángulos. En el caso de un triángulo rectángulo, escribe la longitud de su hipotenusa.

(yo) 7 cm, 24 cm, 25 cm

(ii) 3 cm, 8 cm, 6 cm

(iii) 50 cm, 80 cm, 100 cm

(iv) 13 cm, 12 cm, 5 cm

Solución:

(i) Dado: 7 cm, 24 cm, 25 cm

(25) ² = 25 * 25 = 625

∴Son lados de una recta ∆ e hipotenusa = 625  

(ii) Dado: 3 cm, 8 cm, 6 cm

(8) ² = 8 * 8 = 64  

No son lados del triángulo rectángulo.

(iii) Dado: 50 cm, 80 cm, 100 cm

(100) ² = 100 * 100 = 10000

(50) ²+ (80) ² = 2500 + 6400

Por lo tanto, este no es un triángulo rectángulo.

(iv) Dado: 13 cm, 12 cm, 5 cm

(13) ² = 13 * 13 = 169

(12) ² + (5) ² = 169

Por lo tanto, estos son los lados del triángulo rectángulo y la hipotenusa = 169

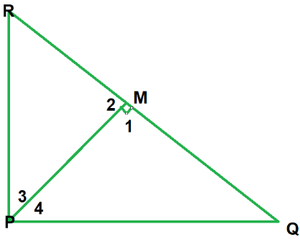
Pregunta 2. PQR es un triángulo rectángulo en P y M es un punto en QR tal que PM ⊥ QR. Demuestre que PM2 = QM × MR.

Solución:

Dado: A ∆PQR recto en ángulo recto en P y PM⊥QR

Para mostrar: PM ² = QM * MR

PM * PM = QM * MR

En ∆PMQ y ∆PMR

∠1 =∠2 -(cada 90°)

∠1 +∠2 +∠3 = 180°

90° + ∠4 + ∠5 = 180°

∠4 +∠5 = 180° – 90°

∠3 + ∠4 = 180° – 90°

∠4 +∠5 = ∠3 +∠4

∴∠5 =∠3  

∴∆PMQ ~ ∆RMP  

  

MP ² = MQ.PM

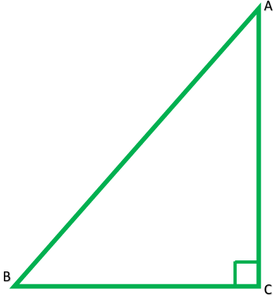
Pregunta 3. En la figura, ABD es un triángulo rectángulo en A y AC ⊥ BD. Muestra esa

(i) AB ² = BC × BD

(ii) CA ² = BC × CC

(iii) AD ² = BD × CD

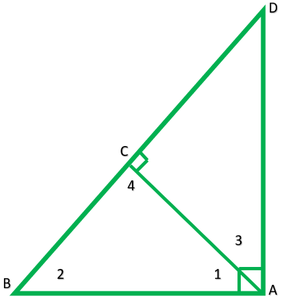
Solución:

Dado: A recto ∆ABD, en ángulo recto en A y AC⊥ BD

Mostrar:  

(i)AB ² = BC × BD

(ii) CA ² = BC × CC

(iii) AD ² = BD × CD

(i) AB ² = BC × BD

AB * AB = BC.BD

En ∆ ABC y ∆ABD

∠B =∠B -(común)

∠BCA = ∠A -(cada 90°)

∴ ∆ABC~∆DBA  

AB ² = BC * DC

(ii) CA ² = BC * CC

CA * CA = BC * CC

En ∆ABC y ∆ACD

∠ACB = ∠ACD -(cada 90°)

En ∆ ACB

∠1 + ∠2 + ∠3 = 180°

∠1 + ∠2 + 90° = 180°

∠1 + ∠2 = 90° -(1)

∠1 + ∠3 = 90° -(2)

∠1 + ∠2 =∠1 + ∠3

∴ ∠2 = ∠3  

∴ ∆ABC~∆DAC  

CA ² = BC * CD

(iii) AD ² = BD × CD

En ∆ABD y ∆ACD

∠A =∠ACD -(cada 90)

∠D =∠D -(común)

∴ ∆ABD~∆CAD -(similitud AA)  

AD ² = BD * CD

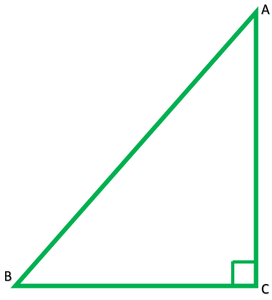
Pregunta 4. ABC es un triángulo isósceles con ángulo recto en C. Demuestra que AB ² = 2AC ² .

Solución:

Dado: ∆ABC en ángulo recto en B

Para probar: AB ² = 2AC ²

Según el teorema de Pitágoras,

(AB) ² = (AC) ² + (BC) ²

(AB) ² = (AC) ² + (AC) ²           -(BC = AC)

^AB2 = 2AC2 ^_

Pregunta 5. ABC es un triángulo isósceles con AC = BC. Si AB ² = 2AC ² , demuestre que ABC es un triángulo rectángulo.

Solución:

Dado: ∆ABC es un triángulo isósceles en el que  

CA = BC

^AB2 = 2AC2 ^_

Para probar: ABCD es correcto ∆  

^AB2 = 2AC2 ^_

AB ² = CA ² + CA ²

∴ Por el contrario del teorema de Pitágoras ∆ACB es un ∆ derecho en C.  

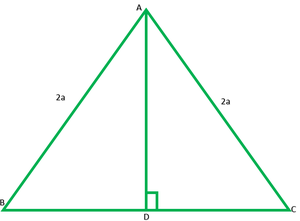
Pregunta 6. ABC es un triángulo equilátero de lado 2a. Halla cada una de sus altitudes.

Solución:

Sea ABC un triángulo equilátero de 2a unidades cada uno

Construcción: Dibuja AD ⊥ BC

A la derecha ∆ ADB

(AB) ² = (AD) ² + (BD) ²

(2a) ² = (AD) ² + (a) ²

(4a) ² = (AD) ² + un ²

4a ² – a ² = (AD) ²

3a ² = (AB) ²

√3 a ² = AD ∴ Cada una de sus alturas= √3 a unidad

√3 a = AD  

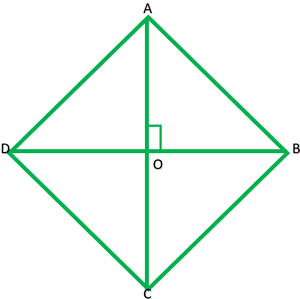
Pregunta 7. Demuestra que la suma de los cuadrados de los lados del rombo es igual a la suma de los cuadrados de sus diagonales.

Solución:

Dado: ABCD es un rombo

Para probar: AB ² + BC ² + CD ² + DA ²

Prueba: ABCD es un rombo y las diagonales AC y BD se bisecan en O.

∴ ∠AOB =∠BOC =∠COD =∠DOA = 90°  

en ∆AOB  

AB2 = ^{AC2 +} BO2 ^_

AB2 = (1/2AC2 ^{) +} (1/ ^2BD2 )

AB2 ⁼ 1/4( ^{AC2 +} BD2 )

4AB ² = AC ² + BD ²          -(1)

De manera similar, en ∆BOC  

4BC ² = AC ² + BD ²          -(2)

4CD ² = CA ² + BD ²          -(3)

4AD ² = CA ² + BD ²          -(4)

Sumar 1, 2, 3 y 4

4AB2 ⁺ 4BC2 + ^{4CD2 +} 4DA2 = 4 ^{( AC2 +} BD2 )

4(AB ² + BC ² + CD ² + DA ² ) = 4(AC ² + BD ² )

∴ AB ² + BC ² + CD ² + DA ² = AC ² + BD ²  

Pregunta 8. En la figura 6.54, O es un punto en el interior de un triángulo diagonal.

(i) OA ² + OB ² + OC ² – OD ² – OE ² – OF ² = AF ² + BD ² + CE ²

(ii) AF ² + BD ² + CE ² = AE ² + CD ² + BF ²

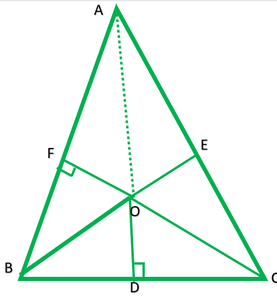
Solución: 

(i) En ∆AFO derecha, por el teorema de Pitágoras  

OA ² = AP ² + OF ²          -(1) 

En la derecha ∆ODB, por el teorema de Pitágoras

OB ² = BD ² + OD ²          -(2)          

En la derecha ∆OEC, por el teorema de Pitágoras

OC ² = CE ² + OE ²          -(3)   

Sumar 1, 2 y 3

OA ² + OB ² + OC ² = AF ² + BD ² + CF ² + OD ² + OE ²

OA ² + OB ² + OC ² – OE ² – OD ² – OE ² = AF ² + BD ² + CE ²

(ii) AF ² + BD ² + CE ² = AE ² + CD ² + BF ²

OB ² = BD ² + OD ²          -(1) 

OC ² = CC ² + OD ²          -(2) 

Restando (1) de (2) obtenemos,

OB ² – OC ² = BD ² + OD ² – (DC ² + OD ² )

= BD ² + OD ² – DC ² – OD ²

= BD ² – CD ²          -(3)      

Similarmente,  

OC ² – AD ² = CE ² – EA ²          -(4) 

AO ² = BO ² = AF ² – FB ²          -(5) 

Sumando 3, 4 y 5, obtenemos,

OB ² – OC ² + OC ² – AO ² + AO ² – BO ² = BD ² – DC ² + CE ² – EA ² + AF ² – FB ²

0 + DC ² + EA ² + FB ² = BD ² + CD ² + AF ²

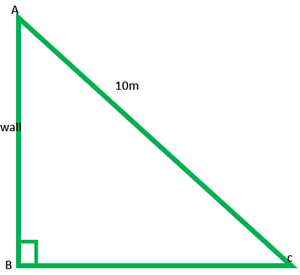
Pregunta 9. Una escalera de 10 m de largo llega a una ventana a 8 m del suelo. Encuentre la distancia del pie de la escalera desde la base de la pared.

Solución:

AB es pared = 8m

AC es escalera = 10m

BC = ?

En derecho ∆ABC, por el teorema de Pitágoras

(AC) ² = (AB) ² + (BC) ²

(10) ² = (8) ² + (BC) ²

100 = 64 + (BC) ²

100 – 64 = (BC) ²

36 = (BC) ²

√36 = BC  

√(6 * 6) = BC

6 = BC  

Por lo tanto, el pie de la escalera está a una distancia de 6 m de la base de la pared.

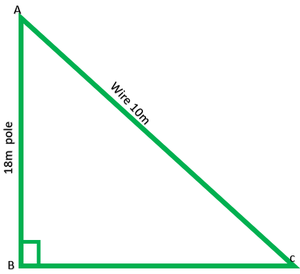
Pregunta 10. Un cable de sujeción sujeto a un poste vertical de 18 m de altura tiene 24 m de largo y tiene una estaca unida al otro extremo. ¿A qué distancia de la base del poste debe clavarse la estaca para que el alambre quede tenso?

Solución:

En la Fig.  

AB es poste = 18m

CA es cable = 24m

BC = ?

En derecho ∆ABC, por el teorema de Pitágoras

(AC) ² = (AB) ² + (BC) ²

(24) ² = (18) ² + (BC) ²

576 = 324 + (AC) ²

576 – 324 = (aC) ²

252 = (AC) ²

√252 = aC  

√(2 * 2 * 3 * 3 * 7) = BC 

2 * 3√7 = BC

6√7 = BC

∴ Por lo tanto, la estaca se puede colocar a una distancia de 6√7 de la base del poste.

Capítulo 6 Triángulos – Ejercicio 6.5 | conjunto 2