Serie de Fibonacci = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …….. Ya se han discutido
diferentes métodos para encontrar el n-ésimo número de Fibonacci . Otra forma sencilla de encontrar el número de Fibonacci enésimo es usar la proporción áurea, ya que los números de Fibonacci mantienen una proporción áurea aproximada hasta el infinito.
Proporción áurea: ![]()
Ejemplos:
Input : n = 9 Output : 34 Input : n = 7 Output : 13
Enfoque:
la proporción áurea puede darnos una respuesta incorrecta.
Podemos obtener el resultado correcto si redondeamos el resultado en cada punto.
nth fibonacci number = round(n-1th Fibonacci number X golden ratio)
fn = round(fn-1 * 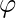 )
)
Hasta el cuarto término, la proporción no se acerca mucho a la proporción áurea (como 3/2 = 1,5, 2/1 = 2, …). Entonces, consideraremos desde el quinto término para obtener el siguiente número de Fibonacci. Para encontrar el noveno número de fibonacci f9 (n = 9):
f6 = round(f5 *) = 8f7 = round(f6 *
) = 13f8 = round(f7 *
) = 21f9 = round(f8 *
) = 34
Nota: Este método puede calcular correctamente los primeros 34 números de Fibonacci. Después de eso, puede haber una diferencia con el valor correcto.
A continuación se muestra la implementación del enfoque anterior:
CPP
// CPP program to find n-th Fibonacci number
#include <bits/stdc++.h>
using namespace std;
// Approximate value of golden ratio
double PHI = 1.6180339;
// Fibonacci numbers upto n = 5
int f[6] = { 0, 1, 1, 2, 3, 5 };
// Function to find nth
// Fibonacci number
int fib(int n)
{
// Fibonacci numbers for n < 6
if (n < 6)
return f[n];
// Else start counting from
// 5th term
int t = 5, fn = 5;
while (t < n) {
fn = round(fn * PHI);
t++;
}
return fn;
}
// driver code
int main()
{
int n = 9;
cout << n << "th Fibonacci Number = " << fib(n) << endl;
return 0;
}
// This code is contributed by Sania Kumari Gupta
// (kriSania804)
C
// C program to find n-th Fibonacci number
#include <math.h>
#include <stdio.h>
// Approximate value of golden ratio
double PHI = 1.6180339;
// Fibonacci numbers upto n = 5
int f[6] = { 0, 1, 1, 2, 3, 5 };
// Function to find nth
// Fibonacci number
int fib(int n)
{
// Fibonacci numbers for n < 6
if (n < 6)
return f[n];
// Else start counting from
// 5th term
int t = 5, fn = 5;
while (t < n) {
fn = round(fn * PHI);
t++;
}
return fn;
}
// driver code
int main()
{
int n = 9;
printf("%d th Fibonacci Number = %d\n", n, fib(n));
return 0;
}
// This code is contributed by Sania Kumari Gupta
// (kriSania804)
Java
// Java program to find n-th Fibonacci number
class GFG
{
// Approximate value of golden ratio
static double PHI = 1.6180339;
// Fibonacci numbers upto n = 5
static int f[] = { 0, 1, 1, 2, 3, 5 };
// Function to find nth
// Fibonacci number
static int fib (int n)
{
// Fibonacci numbers for n < 6
if (n < 6)
return f[n];
// Else start counting from
// 5th term
int t = 5;
int fn = 5;
while (t < n) {
fn = (int)Math.round(fn * PHI);
t++;
}
return fn;
}
// Driver code
public static void main (String[] args)
{
int n = 9;
System.out.println(n + "th Fibonacci Number = "
+fib(n));
}
}
// This code is contributed by Anant Agarwal.
Python3
# Python3 code to find n-th Fibonacci number # Approximate value of golden ratio PHI = 1.6180339 # Fibonacci numbers upto n = 5 f = [ 0, 1, 1, 2, 3, 5 ] # Function to find nth # Fibonacci number def fib ( n ): # Fibonacci numbers for n < 6 if n < 6: return f[n] # Else start counting from # 5th term t = 5 fn = 5 while t < n: fn = round(fn * PHI) t+=1 return fn # driver code n = 9 print(n, "th Fibonacci Number =", fib(n)) # This code is contributed by "Sharad_Bhardwaj".
C#
// C# program to find n-th Fibonacci
// number
using System;
class GFG {
// Approximate value of golden ratio
static double PHI = 1.6180339;
// Fibonacci numbers upto n = 5
static int []f = { 0, 1, 1, 2, 3, 5 };
// Function to find nth
// Fibonacci number
static int fib (int n)
{
// Fibonacci numbers for n < 6
if (n < 6)
return f[n];
// Else start counting from
// 5th term
int t = 5;
int fn = 5;
while (t < n) {
fn = (int)Math.Round(fn * PHI);
t++;
}
return fn;
}
// Driver code
public static void Main ()
{
int n = 9;
Console.WriteLine(n + "th Fibonacci"
+ " Number = " + fib(n));
}
}
// This code is contributed by vt_m.
PHP
<?php
// PHP program to find n-th
// Fibonacci number Approximate
// value of golden ratio
$PHI = 1.6180339;
// Fibonacci numbers
// upto n = 5
// Function to find nth
// Fibonacci number
function fib ($n)
{
global $PHI;
$f = array(0, 1, 1, 2, 3, 5);
// Fibonacci numbers
// for n < 6
if ($n < 6)
return $f[$n];
// Else start counting
// from 5th term
$t = 5;
$fn = 5;
while ($t < $n)
{
$fn = round($fn * $PHI);
$t++;
}
return $fn;
}
// Driver Code
$n = 9;
echo $n, "th Fibonacci Number = ",
fib($n), "\n";
// This code is contributed by aj_36
?>
Javascript
<script>
// JavaScript program to find n-th Fibonacci number
// Approximate value of golden ratio
let PHI = 1.6180339;
// Fibonacci numbers upto n = 5
let f = [ 0, 1, 1, 2, 3, 5 ];
// Function to find nth
// Fibonacci number
function fib (n)
{
// Fibonacci numbers for n < 6
if (n < 6)
return f[n];
// Else start counting from
// 5th term
let t = 5, fn = 5;
while (t < n) {
fn = Math.round(fn * PHI);
t++;
}
return fn;
}
// driver code
let n = 9;
document.write(n + "th Fibonacci Number = " + fib(n) + "<br>");
// This code is contributed by Mayank Tyagi
</script>
Producción:
9th Fibonacci Number = 34
Podemos optimizar el trabajo de solución anterior en O (Log n) mediante el uso de un método eficiente para calcular la potencia .
Es posible que el método anterior no siempre produzca resultados correctos, ya que se trata de cálculos de coma flotante. Esta es la razón por la que este método no se usa en la práctica, incluso si se puede optimizar para que funcione en O (Log n). Consulte el siguiente video del MIT para obtener más detalles.
https://www.youtube.com/watch?v=-EQTVuAhSFY
Publicación traducida automáticamente
Artículo escrito por Sukanta_it y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA