Juggler Sequence es una serie de números enteros en los que el primer término comienza con un número entero positivo a y los términos restantes se generan a partir del término inmediatamente anterior utilizando la siguiente relación de recurrencia: 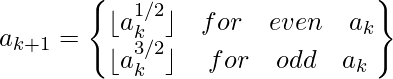
Juggler Sequence que comienza con el número 3:
5, 11, 36, 6, 2, 1
Secuencia malabarista que comienza con el número 9:
9, 27, 140, 11, 36, 6, 2, 1
Dado un número n , tenemos que imprimir la Secuencia malabarista para este número como el primer término de la secuencia.
Ejemplos:
Input: 9 Output: 9, 27, 140, 11, 36, 6, 2, 1 We start with 9 and use above formula to get next terms. Input: 6 Output: 6, 2, 1
C++
// C++ implementation of Juggler Sequence
#include <bits/stdc++.h>
using namespace std;
// This function prints the juggler Sequence
void printJuggler(long long n)
{
long long a = n;
// print the first term
cout << a << " ";
// calculate terms until
// last term is not 1
while (a != 1)
{
long long b = 0;
// Check if previous term
// is even or odd
if (a % 2 == 0)
// calculate next term
b = floor(sqrt(a));
else
// for odd previous term
// calculate next term
b = floor(sqrt(a) *
sqrt(a) * sqrt(a));
cout << b << " ";
a = b;
}
}
// Driver Code
int main()
{
printJuggler(37);
cout <<"\n";
printJuggler(9);
return 0;
}
// This code is contributed by shubhamsingh10
C
// C implementation of Juggler Sequence
#include<stdio.h>
#include<math.h>
// This function prints the juggler Sequence
void printJuggler(int n)
{
int a = n;
// print the first term
printf("%d ", a);
// calculate terms until last term is not 1
while (a != 1)
{
int b = 0;
// Check if previous term is even or odd
if (a%2 == 0)
// calculate next term
b = floor(sqrt(a));
else
// for odd previous term calculate
// next term
b = floor(sqrt(a)*sqrt(a)*sqrt(a));
printf("%d ", b);
a = b;
}
}
//driver program to test above function
int main()
{
printJuggler(3);
printf("\n");
printJuggler(9);
return 0;
}
Java
// Java implementation of Juggler Sequence
import java.io.*;
import java.math.*;
class GFG {
// This function prints the juggler Sequence
static void printJuggler(int n)
{
int a = n;
// print the first term
System.out.print(a+" ");
// calculate terms until last term is not 1
while (a != 1)
{
int b = 0;
// Check if previous term is even or odd
if (a%2 == 0)
// calculate next term
b = (int)Math.floor(Math.sqrt(a));
else
// for odd previous term calculate
// next term
b =(int) Math.floor(Math.sqrt(a) *
Math.sqrt(a) * Math.sqrt(a));
System.out.print( b+" ");
a = b;
}
}
// Driver program to test above function
public static void main (String[] args) {
printJuggler(3);
System.out.println();
printJuggler(9);
}
}
//This code is contributed by Nikita Tiwari.
Python3
import math #This function prints the juggler Sequence def printJuggler(n) : a = n # print the first term print (a,end=" ") # calculate terms until last term is not 1 while (a != 1) : b = 0 # Check if previous term is even or odd if (a%2 == 0) : # calculate next term b = (int)(math.floor(math.sqrt(a))) else : # for odd previous term calculate # next term b = (int) (math.floor(math.sqrt(a)*math.sqrt(a)* math.sqrt(a))) print (b,end=" ") a = b printJuggler(3) print() printJuggler(9) # This code is contributed by Nikita Tiwari.
C#
// C# implementation of Juggler Sequence
using System;
class GFG {
// This function prints the juggler Sequence
static void printJuggler(int n)
{
int a = n;
// print the first term
Console.Write(a+" ");
// calculate terms until last term is not 1
while (a != 1)
{
int b = 0;
// Check if previous term is even or odd
if (a%2 == 0)
// calculate next term
b = (int)Math.Floor(Math.Sqrt(a));
else
// for odd previous term calculate
// next term
b =(int) Math.Floor(Math.Sqrt(a) *
Math.Sqrt(a) * Math.Sqrt(a));
Console.Write( b+" ");
a = b;
}
}
// Driver Code
public static void Main () {
printJuggler(3);
Console.WriteLine();
printJuggler(9);
}
}
// This code is contributed by Nitin Mittal
PHP
<?php
// PHP implementation of
// Juggler Sequence
// function prints the
// juggler Sequence
function printJuggler($n)
{
$a = $n;
// print the first term
echo($a . " ");
// calculate terms until
// last term is not 1
while ($a != 1)
{
$b = 0;
// Check if previous
// term is even or odd
if ($a % 2 == 0)
// calculate next term
$b = floor(sqrt($a));
else
// for odd previous term
// calculate next term
$b = floor(sqrt($a) * sqrt($a) *
sqrt($a));
echo($b . " ");
$a = $b;
}
}
// Driver Code
printJuggler(3);
echo("\n");
printJuggler(9);
// This code is contributed by Ajit.
?>
Javascript
<script>
// Javascript implementation of Juggler Sequence
// This function prints the juggler Sequence
function printJuggler(n)
{
let a = n;
// print the first term
document.write(a+" ");
// calculate terms until last term is not 1
while (a != 1)
{
let b = 0;
// Check if previous term is even or odd
if (a%2 == 0)
// calculate next term
b = Math.floor(Math.sqrt(a));
else
// for odd previous term calculate
// next term
b = Math.floor(Math.sqrt(a) *
Math.sqrt(a) * Math.sqrt(a));
document.write( b+" ");
a = b;
}
}
// Driver code to test above methods
printJuggler(3);
document.write("<br/>");
printJuggler(9);
// This code is contributed by avijitmondal1998.
</script>
Producción:
3 5 11 36 6 2 1 9 27 140 11 36 6 2 1
Complejidad de tiempo : O (nlogn) ya que usar un solo ciclo while y encontrar la raíz cuadrada toma tiempo logarítmico.
Complejidad espacial : O(1) para variables constantes
Puntos importantes:
- Los términos en Juggler Sequence primero aumentan hasta un valor máximo y luego comienzan a disminuir.
- El último término en Juggler Sequence siempre es 1.
Referencia:
https://en.wikipedia.org/wiki/Juggler_sequence
Este artículo es una contribución de Harsh Agarwal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA